4.1.2　直接三角剖分法构建地质界面

最简单的地质表面是圆柱形的，它可以由折线和其展开向量来定量描述，或者通过多条平行线来构建分段锥形面来描述。圆柱形假设通常被用来建立地质界面模型。然而，这些可用数学公式描述的理想型地质界面实际上几乎是不存在的（Pollard et al.，2005）。

对于一个简单的，或者可以说起伏比较小的地质界面，比较令人接受的地质界面构建方法是在地质界面的分布范围内将采样点的高程值进行三角剖分，从而建立起一个比较顺滑的地质表面。基于德洛奈三角剖分的不规则三角网格曲面是最常用的方法，因为它可以最大限度地保证三角形网格的质量（Peucker et al.，1978）。德洛奈三角剖分的一个缺点是它的边界是一个凸壳，因此利用它建立的曲面可能会超过实际的地质边界。一个实用的解决方案是引入一条通过地质边界数字化而来的多边形曲线作为约束，以避免过界。因此，地质边界模型的建立是将每一个地质曲面限制在自己区域内的有效手段。从几何的角度来看，任意两种边界线有三种可能的关系：在某些节点相交、部分或全部重叠、无连接。在建模之前，建议构建一个完整的二维线框模型，该模型中包括所有被模拟的地质界面的外边界。该线框模型遵守在第2.2节中所介绍的地质边界的基本规则，可以有效避免各地质单元之间违背自然规律的接触，从而提高三维地质模型的准确性（Xu et al.，2011）。

直接三角剖分法可以连接所有输入的采样点，如图4-1所示。因此，由此构建的地质界面刚好可以对应每个采样点的高程，在每一个三角形范围内的地形是一个平面。然而，输入点往往采用不规则采样，有时某些三角形的范围非常大，这将直接降低地质界面的质量。此外，所创建的地质界面的地形特征只取决于输入点的特征，而不依赖于地质界面的真实特征。因此，在构造地质界面前，需提高输入点的质量和分布密度。

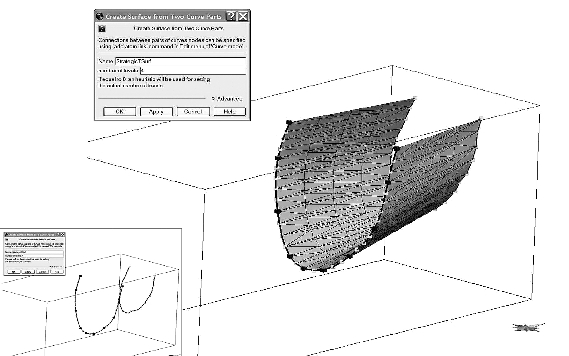
图4-1　直接三角剖分法构建地质界面