5.1.4 研究区基岩上岩土体三维地层结构模型构建
根据钻孔记录及二维地质图,第四纪沉积物几乎遍布整个建模区域。然而,根据搜集到的钻孔记录,无法区分回填土、全新世单元和更新世单元之间的确切边界。因此,第四纪沉积物将被设定为单一的地质体,其上下边界分别为地球表面和白垩纪的顶部。研究区有三个地层界面需要采用地质统计学方法进行建模,分别为主火车站地区和Burtscheid地区的Hergenrath组地层,以及Laurensberg断层上盘的Aachen组砂层(见图5-3)。
地质统计学方法通过半变差函数量化数据的空间结构,进行预测。根据这一方法,本案例分析并预测了三个地层界面上边界高程起伏的结构特征。
三组高程数据的描述性统计特征如表5-2所示。分布在三个不同区域两个地层的高程平均值和标准方差彼此不同,应分别分析三个地层界面的空间变异性。
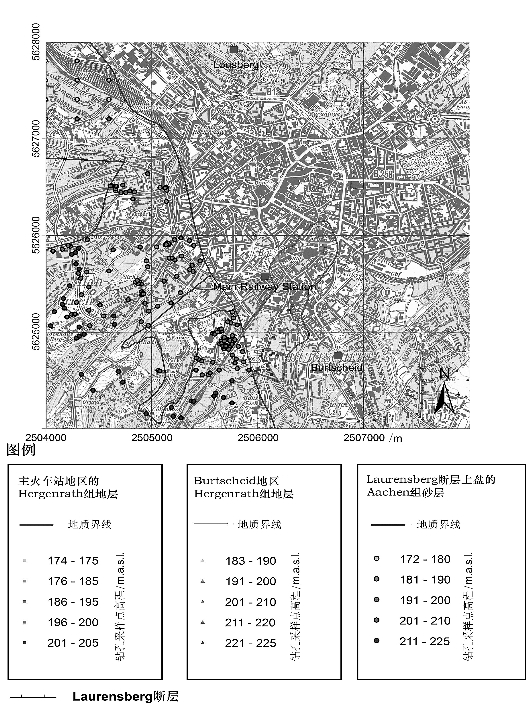
图5-3 主火车站地区和Burtscheid地区的Hergenrath组地层,以及Laurensberg断层上盘Aachen组砂层地质边界线及钻孔分布图
表5-2 三组高程数据的描述性统计特征
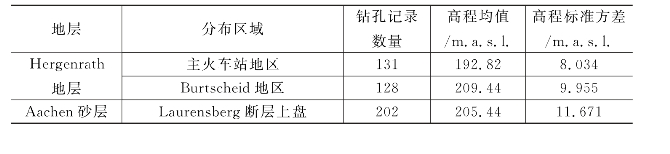
在三维坐标系统中绘制从岩芯记录中读取的两个地层上边界的高程点数据集,然后投射到垂直的xz和yz 平面上以识别投影点沿着两个方向的倾斜程度,并检查数据是否满足地质统计学的二阶平稳假设。主火车站地区的Hergenrath组地层的数据投影点在xz 和yz 平面上呈现明显的倾斜形状,适合使用二阶多项式来计算该趋势。Burtscheid地区的Hergenrath组地层顶部的数据投影点在yz平面上呈现明显的斜率,而在xz 平面上呈现几乎水平的线,这意味着一阶多项式就可以计算出这一趋势。Laurensberg断层上盘的Aachen组砂层上边界的高程数据在xz和yz 平面上的投影均呈现明显的谷形,三次多项式适合于描述这一趋势。
趋势在一个高程数据集中是非随机的,可以用数学公式表示,不需要用克里金插值来预测。因此,在进行变量的结构分析之前,应从采样高程点数据集中消除该趋势。剩余的高程点数据集称为残余数据集。三个残余数据集遵循二阶平稳假设,可对其采用变差函数分析。
三个待插值界面的高程采样点计算出来的变差函数曲面如图5-4所示,采样数据集的各向异性或各向同性特征可从变差函数曲面看出。图5-4中符号“▲”所指示的是协方差值,实线代表最大连续性方向,虚线代表最小连续性方向。表5-3和图5-5分别描述三个待插值界面高程变量的结构模型。
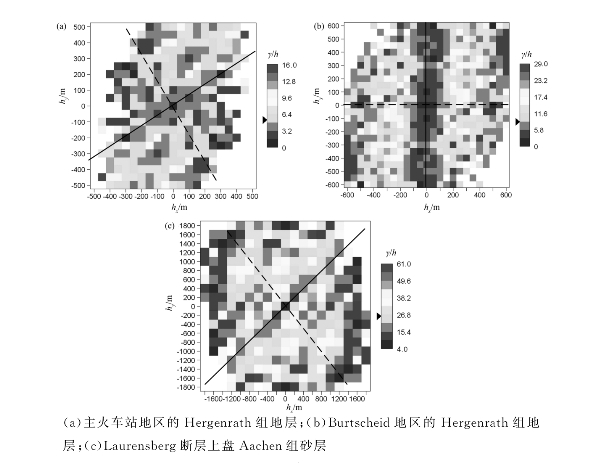
图5-4 采样点高程变差函数曲面
表5-3 三个待插值地层界面的结构变差函数
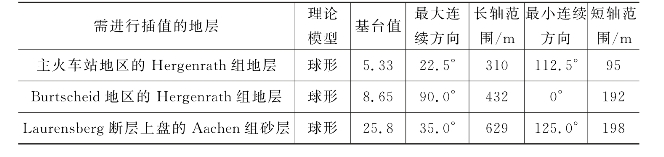
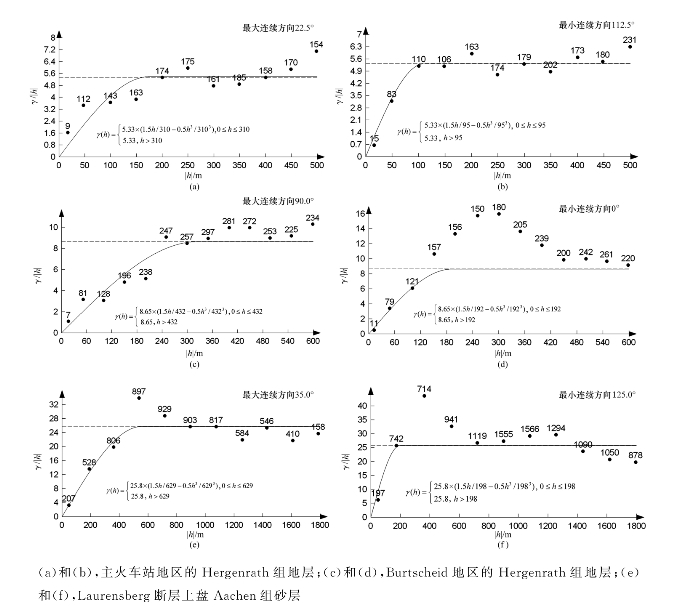
图5-5 三个待插值地层界面的试验变差函数(点)和理论模型(线)
对图5-5中采用的结构模型的理解如下。
(1)空间相关性随着相隔距离的增大而减小,直到不存在空间相关性为止。虽然相关范围取决于距离,但相关性降低的性质在不同的方向上是相同的,称为几何各向异性。(https://www.daowen.com)
(2)根据对主火车站地区Hergenrath组地层上边界采样高程点数据集的变差函数分析可得,高程数据的空间变异呈各向异性。最大连续性沿着22.5°方向(均为逆时针方向),最小连续性沿着112.5°方向[见图5-4(a)]。存在协方差,其值为5.33。对该地层界面进行克里金插值,其搜索邻域为椭圆形,长轴沿着最大连续性方向,半径为310m,短轴沿着最小连续性方向,半径为95m。沿着长轴,高程值发生轻微变化,沿着短轴(西北—东南),高程值迅速变化。
(3)根据Burtscheid地区的Hergenrath组地层上边界采样高程点数据集的变差函数分析可得,高程数据的空间变异性呈各向异性。最大连续性沿着90.0°方向,最小连续性沿着0°方向[见图5-4(b)]。存在协方差,其值为8.65。对该地层界面进行克里金插值,其搜索邻域为椭圆形,长轴沿着最大连续性方向,半径为432m,短轴沿着最小连续性方向,半径为192m。Burtscheid地区的地面高度从南向北逐渐降低,这与最大连续性的方向相对应。
(4)根据Laurensberg断层上盘的Aachen组砂层上边界采样高程点数据集的变差函数分析可得,高程数据的空间变异性是各向异性的。最大连续性沿着35.0°方向,最小连续性沿着125.0°方向[见图5-4(c)]。存在协方差,其值为25.8。对该地层界面进行克里金插值,其搜索邻域为椭圆形,长轴沿着最大连续性方向,半径为629m,短轴沿着最小连续性方向,半径为198m。在Laurensberg断层的顶壁中存在一些凹陷,两个重要方向对应于这些凹陷的方向,如图5-1所示。
通用克里金法适用于预测趋势函数的趋势已知和回归系数未知的变量(Deutsch,2014)。对于三个待插值地层边界,克里金插值法采用了由采样点拟合的结构特征函数的理论模型(见表5-3和图5-5),然后分别进行交叉验证,以评估理论模型预测的能力。对于提供准确预测的两种理论模型,平均误差应接近0,均方根误差和平均标准误差应尽可能小,均方根标准误差应接近1。由于在数据集中有趋势的存在,在此采用了通用克里金法。待插值的三个地层界面上边界的高程预测图分别如图5-6至5-8所示,预测误差统计如表5-4所示。
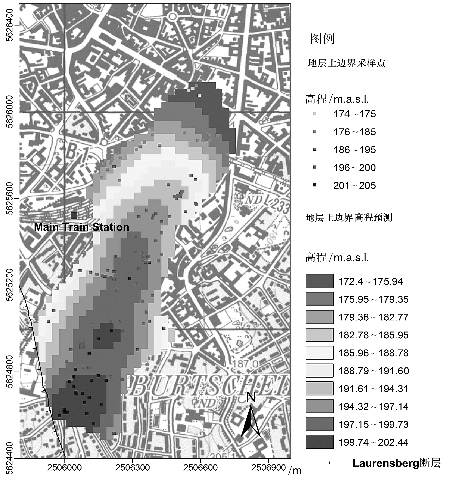
图5-6 主火车站地区的Hergenrath组地层上边界高程预测图
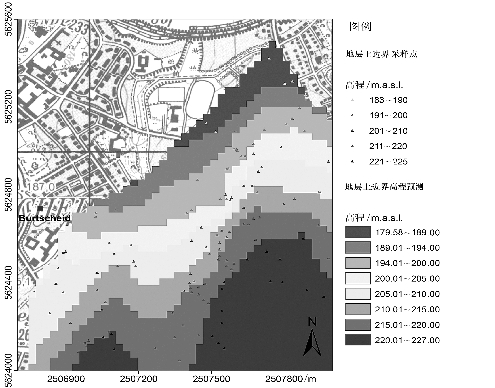
图5-7 Burtscheid地区的Hergenrath组地层上边界高程预测图
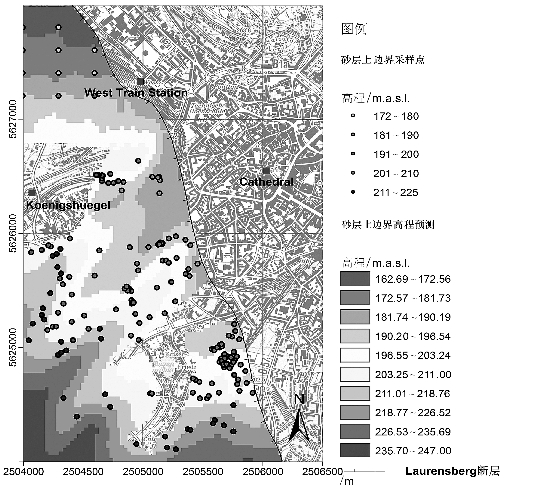
图5-8 Laurensberg断层上盘的Aachen组砂层上边界高程预测图
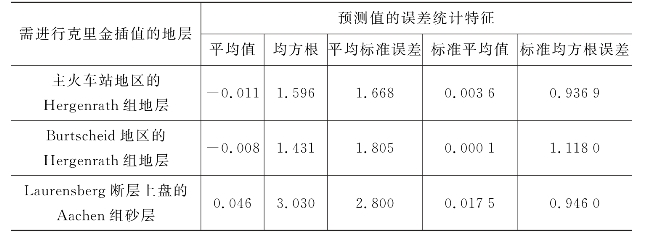
表5-4 交叉验证得到的预测误差统计特征
将图5-6至5-8栅格化,单元格大小设为30m×30m,提取每个单元格中心的x,y,z坐标数据,导入建模软件中,构建地层界面,如图5-9所示。
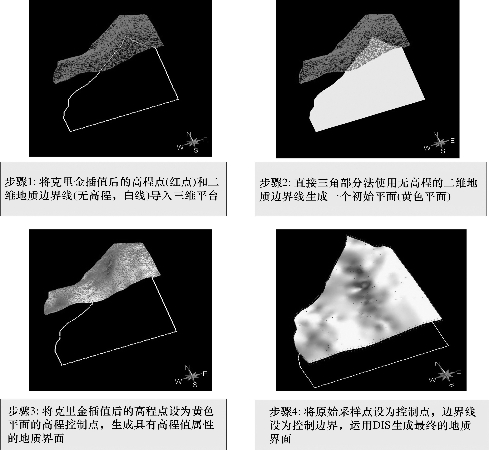
图5-9 地层界面构建和优化过程
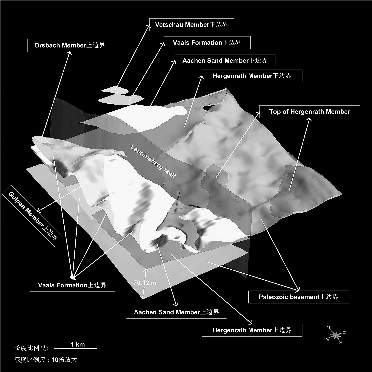
图5-10 研究区建模区域的三维地层结构模型(表面DEM 未显示)
建模区域所有重要地质单元的结构模型如图5-10所示。所得到的三维地层结构模型的厚度在Laurensberg 断层的上盘为36.94~124.45m,有Laurensberg断层的下盘为1.92~123.35m。研究区的块体模型是通过地质单位顶部边界和底部边界的组合构建的。结构模型是至关重要的,在其构建过程中,违反自然规律和地质历史规律的交叉点将被检验并优化。
