4.1.4 地质统计学
克里金插值是地质统计学分析的一个步骤。地质统计学(geostatistics)于20世纪50年代初开始形成,20世纪60年代,是在法国著名统计学家乔治斯·马瑟龙(Georges Matheron)的大量理论研究工作基础上形成的一门新的统计学分支。由于它首先是在地学领域,如采矿学、地质学等中发展和应用的,因此得名地质统计学。地质统计学的特点是它研究的变量不是纯随机变量,而是空间变量。地质统计学中的空间变量具有四个特点:①该空间变量根据其在一个域内的空间位置不同而取不同的值,它是随机变量与位置有关的随机函数,因此它既有随机性又有结构性;②地质统计学研究的变量不能进行如经典统计学变量一样的重复试验,因为空间变量一旦在某一空间位置上取得一个样品后,就不可能在同一位置再次取到该样品;③空间变量是在空间不同位置取样,因而相邻样品中的值不一定保持独立,会具有某种程度的空间相关性;④地质统计学除了要考虑样本的数字特征外,更主要的是研究空间变量的空间分布特征,因此,地质统计学研究主要围绕着变量空间分布理论和估计方法。典型的地质统计学分析过程如图4-2所示。

图4-2 典型地质统计学分析过程
本书中介绍的地质统计学步骤摘自一些地质统计学教科书和期刊论文(Gringarten et al.,2001;Deutsch,2014;Goovaerts,1997;王政权,1999)。地质统计学还被定义为一种基于空间变量理论和变差函数工具,对随机和结构自然现象进行分析的科学(Webster,1985;侯景儒,1990)。地质统计学的两个基本组成部分是:①空间变量,在空间和/或时间上变化并自相关的现象;②(半)变差函数,用于表征空间相关性或空间变量粗糙程度的工具。
4.1.4.1 变量的基本要求
地质统计学要求空间变量符合平稳假设。对于随机变量Z(u),如果Z(ui)的累积分布等于Z(ui+ h)的累积分布,则变量满足严格的平稳假设。即
![]()
其中,u 是空间坐标的向量,Z(u)是将所考虑的变量作为空间位置的函数,h 代表两个空间位置之间间隔的滞后向量,函数F u1,u2,…,un(Z 1,Z 2,…,Zn)为累积分布函数。空间变量通常无法遵守严格的平稳假设,在实践中如果其能满足二阶平稳假设,就可以采用地质统计学方法来估算它。当空间变量Z(u)满足以下两个条件时,它就是二阶平稳的。
(1)在研究区域中,Z(u)的数学期望值存在且为一常数,即
![]()
(2)在研究区域中,Z(u)的协方差存在仅取决于滞后向量h,而不是位置u,即
![]()

其中,m 是常数值,E[Z(u)]是变量Z(u)的数学期望值,Cov{Z(u),Z(u+ h)}是Z(u)和Z(u+ h)的协方差函数,C(h)是距离h 的协方差,Var[Z(u)]是Z(u)的方差。
在二阶平稳假设中,假定协方差Cov{Z(u),Z(u+ h)}存在。在本质上,许多随机变量并不具有协方差,但是可以找到它们的变差函数值。因此,提出一个更弱的平稳假设,即内在假设。
如果空间变量Z(u)满足下列两个条件,则满足内在假设。
(1)在研究区域中,[Z(u)- Z(u+ h)]的数学期望值等于零,E[Z(u)]不需要存在或作为常数,即
![]()
(2)[Z(u)- Z(u+ h)]的方差存在并且稳定(不依赖于位置),即
![]()
地质统计学的第一步是检查所研究的空间变量是否遵循上述假设。如果不遵循,应进行适当的转换使得研究变量符合上述假设。
4.1.4.2 趋势消除
数据中存在的集中趋势是非随机性的,可以用数学公式来表示而不需要进行估算(Goovaerts,1997)。当空间变量的数据存在趋势时,其无法满足地质统计学中的固定假设。因此,样本中的空间趋势应在进行变差函数分析之前被识别并去除。在目前的研究中,可将地面高程点绘制在三维空间中,将其投影到XZ 和YZ 的两个垂直平面上。通过每个平面上的投影点还原到最佳拟合线,并选择多项式函数来描绘该线。然后从样本中去除空间趋势,剩余的随机部分被称为残差,被用于后续插值。
4.1.4.3 (半)变差函数分析
基于残差值的半变差函数进行空间变量的结构分析,这是地质统计学中独有的方法。多年以来,半变差函数被广泛用于量化空间现象的空间变异性。半变差函数γ(h)是点与点之间距离的分离函数,而不是特定位置的函数,其定义为
![]()
![]()
在内在假设条件下,E[Z(u)- Z(u+ h)]= 0,因此
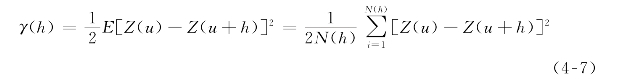
其中,N(h)是由距离h 所分隔的数据对的数量。
在二阶平稳假设下,γ(h)= C(0)- C(h),如图4- 3所示。
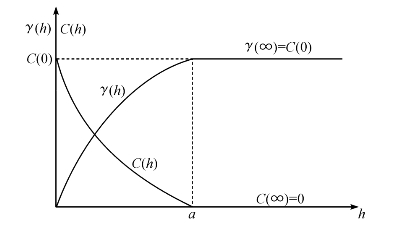
图4-3 二阶平稳假设下半变差函数值和协方差之间的关系
当两点之间的滞后距离h 增加时,半变差函数值增加。但是,它随后将呈平稳状态,并在距离超过a时达到最大值C(0)。当两点之间的滞后距离h 增加时,协方差减小,而后协方差C(h)将趋于平稳,在距离超过a后C(h)将达到零。这里的a值被称为范围,反映了自相关的影响频谱。当距离在0到a 之间时,空间变量是自相关的。通过半变差函数γ(h),可以计算一组向量中滞后距离为h 的所有点对的半变差函数值。一系列滞后距离h 的半方差可以绘制为二维图,即变差函数二维图,如图4-4(a)所示。变差函数二维图的每个单元代表空间连续性的测量值,对分离向量h 的半变差函数值进行了汇总。如果半变差函数值在所有方向上都表明相同的分布结构,则残差值在所有方向上具有相同的空间连续性,或是各向同性,相反,则是各向异性的。各向异性在空间现象中很常见。在这种情况下,可以从变差函数二维图中识别最大和最小空间连续性的方向。例如,在图4- 4(a)中,最大连续性沿着实线方向,最小连续性沿着虚线方向。然后沿着两个方向的半变差函数值绘制在二维坐标系中,其中x 轴为滞后距离h,y 轴为半变差函数值,如图4-4(b)中的点所示。这些由一系列滞后距离h 计算出的半变差函数值称为试验值。试验值是通过有限的样本值计算出来的,为了用将从样本中探索到的空间相关性描述空间变量在整个建模区域中的结构特征,可用试验值来拟合出一个理论模型[见图4-4(b)中的曲线]。
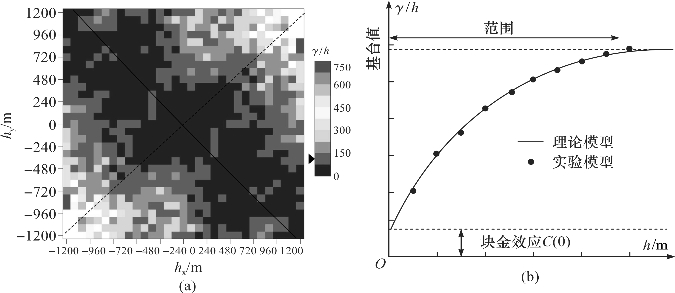
图4-4 (a)变差函数二维图(Dong et al.,2011)
(b)试验变差函数值及拟合的理论模型(王政权,1999)
理论模型中需包含下面三个重要参数。(https://www.daowen.com)
(1)基台值(sill value)。它是当变差函数的曲线呈水平状态时空间变量的半变差函数值。基台值由块金值和协方差两部分组成。块金值(nugget value)反映了两个非常接近的位置处变量方差值的变化,有时由观测误差或最小范围滞后距离内的数据对缺乏而引起。基台值表达的是测量样本之间的最大自相关性。
(2)范围(range)。范围是半变差函数值达到基台值时的滞后距离。据推测,当两个样本的距离超出该范围时,它们不是自相关的。
(3)模型类型。五种最常用的模型是块金、球形、指数、高斯和幂模型。可以构建这些模型的线性组合以适应复杂的半变差函数结构(嵌套结构)。块金模型表示因小规模变化而导致的不连续性,独立的块金模型不能代表空间自相关变量。球形模型可以在特定范围内精确地达到指定基准值。指数和高斯模型逐渐地接近基台,两个模型中的范围被定义为半变差(变异)值达到了基台值的95%。这些模型的数学公式如下。
块金模型:

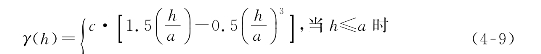
球形模型:
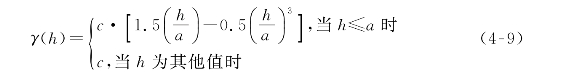
指数模型:
![]()
高斯模型:
![]()
幂模型:
![]()
其中,c为基台值,w为幂指数。
具有有限基值台的模型称为过渡模型,如球形、指数和高斯模型,三种模型如图4-5所示。
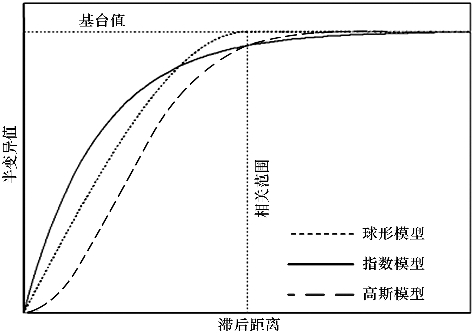
图4-5 三种常用的理论模型
空间变量结构特征的理论模型可直接用于克里金插值中。对于一个未知位置而言,对其属性值的估计是在有限邻域内进行的,该搜索邻域由空间变量的最大连续性和最小连续性方向的长距离和短距离来定义,如图4-6所示。图4-6中,椭圆是被估计节点(交叉红点)的邻域搜索边界。
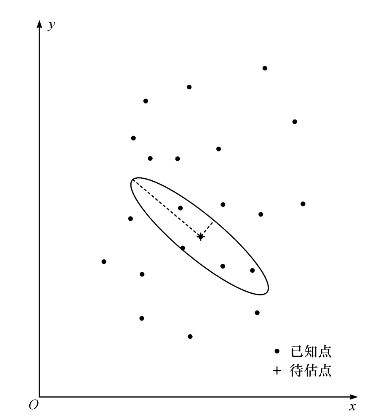
图4-6 被估计点的搜索邻域
4.1.4.4 克里金插值法
插值方法估算的结果是相邻样本的线性组合,其定义为
![]()
其中,Z*(x 0)是估计值,λi是邻近样本的权重,Z(x i)是邻近样本的测量值。预测误差的无偏性和最小方差是λi选择的两个基本要求。
(1)无偏性:
![]()
(2)最小方差:
![]()
基于这两个要求,可以得到一个计算估计位置相邻样本权重的方程组。方程组的解是权重λi和预测方差。方程组由马瑟龙创建并阐述(Matheron,1963)。
为了对地质表面进行建模,首先要定义覆盖表面范围的一组节点的格状网(见图4-7),然后估算网络中每个节点的值。
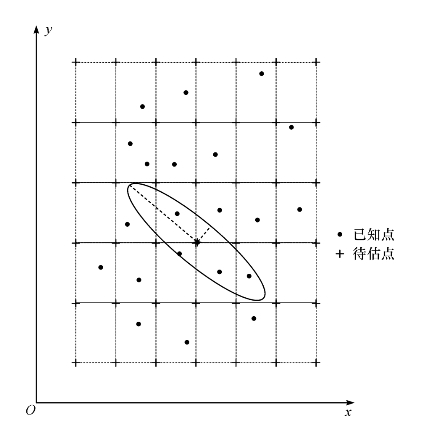
图4-7 克里金插值网格
克里金插值法已经演变为多种形式,可根据空间变量的不同特征进行选取。经典的方法是简单克里金法(simple kriging,SK)、普通克里金法(ordinary kriging,OK)、通用克里金法(universal kriging,UK)、协 同克里金 法(cokriging,CK)和指标克里金法(indicator kriging,IK)。简单克里金法要求空间变量的数学期望值是平稳的并且为已知常数;普通克里金法要求空间变量的数学期望值是平稳但未知的;通用克里金法要求空间变量的数学期望值为位置的函数;协同克里金法考虑了几个变量的自相关性,并使用其他变量来估算其中一个主要的变量,该法不仅需要估计每个变量的自相关性,还需要考虑变量之间的互相关性;指标克里金法通过使用连续数据的临界值将数据转换为二进制数据的0或1,估算值将在0和1之间,并且指标克里金法的估算值可以解释为变量大于或小于临界值的概率。
克里金插值法最后一个关键步骤是交叉验证,用于考量理论模型的预测能力。要执行交叉验证,首先将一个点从样本数据集中删除,然后再估算这个被删除的值。分段进行相同的程序后,每个样本将拥有一个真实值和一个估算值,这两个值的区别称为误差。对误差进行统计,可以得出一些有意义的统计因素,如平均误差(mean error,ME)和均方根误差(root mean square error,RMSE)。最优估计是ME等于零,RMSE为最小值。为了实现最优估计,可以选择多种理论模型来执行克里金插值法,通过比较ME和RMSE可以找到最佳的理论模型。
以北京市顺义新城(1)层人工填土为例,在建模中,原始采样点直接生成的层面如图4-8所示。从图4-8中可以看出,剖分网格比较大,地层层面起伏处棱角尖锐。由克里金法插值后的点生成的层面如图4-9所示,可以看出,剖分网格小而密,地层层面起伏处较平缓,能较好地反映地层实际情况。
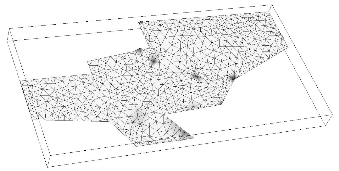
图4-8 原始采样点建立的层面
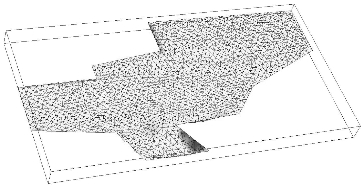
图4-9 经克里金插值后的点构建的层面
