5.1.6 模型定量评估
对三维地质模型的质量评估主要是评价模型中各种预测的不确定性。由于地下信息的不完全可见性,不确定性是三维地质模型的固有属性。将不确定性评估值作为一种属性参数赋予三维地质模型,可构建三维不确定性模型。城市环境中三维地质建模产品最终都要为城市规划和建设服务,是许多关系到人民和社会安全的重要决策的基础框架。因此,决策者需明确使用的三维地质模型中数据的质量和可靠度。
量化评估模型质量的第一个步骤是明确不确定性产生的原因,其次是确定关键因素并考虑各因素之间的关系。地质条件或岩土性质的不确定性可以分为随机(偶然)不确定性和主观(认识论)不确定性两种。随机不确定性代表研究对象的自然随机性,它可用空间变异性的函数来表示,这种不确定性无法减少或消除。主观不确定性是由信息缺乏、测量及计算手段的缺陷引起的(Lacasse et al.,1997)。未知的参数是根据有限的采样数据进行估算的,因此存在采样不确定性。测量不确定性是由测试仪器、量化方法、数据记载、现场调查人员的专业程度的不确定引起的。通过搜集更多数据、改进建模或测量方法可减少主观不确定性。因此,目前可以从两个方面对区域尺度三维地质模型的不确定性来源进行探讨。引起研究区三维地质模型不确定性的所有因素及各因素之间的关系如图5-21所示,其可以作为不确定性来源因素的概念模型。
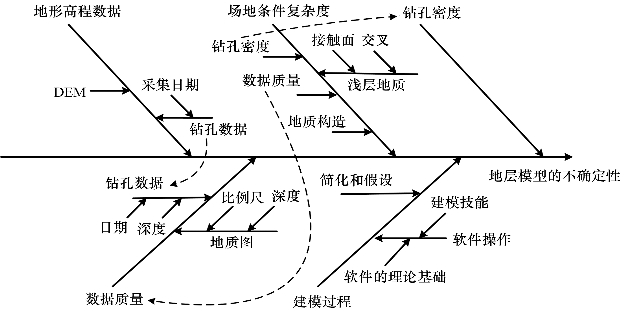
图5-21 研究区地层界面不确定性因素
经分析,研究区三维地质模型的不确定性的主要来源为数据密度、地质条件复杂程度和插值过程。由于在数据管理阶段严格检测了钻孔记录的质量,移除了质量较差的数据,在本案例中数据本身质量不作为不确定性的来源。来源和不确定性之间的关系可表述如下:①如果数据密度较高,则预测的不确定性较低(反之亦然);②如果地质条件复杂程度低,则不确定性较低(反之亦然)。
5.1.6.1 数据密度
对于第5.1.4节中插值的三个地质界面上边界,最优的预测用于建立三维地质模型。最优意味着平均误差最接近零,均方根误差最小。克里金预测标准误差是克里金方差的平方根,代表着真实值和预测值之间的差别。因此,可用克里金预测标准误差值来量化预测的不确定性。克里金预测标准误差与样本到预测值的距离有关,与特定的高程值无关,它也可以揭示数据密度对预测质量的影响。主火车站地区的Hergenrath地层、Burtscheid地区的Hergenrath地层以及Laurensberg断层上盘的Aachen砂层上边界的预测标准误差网格图分别如图5-22至5-24所示。
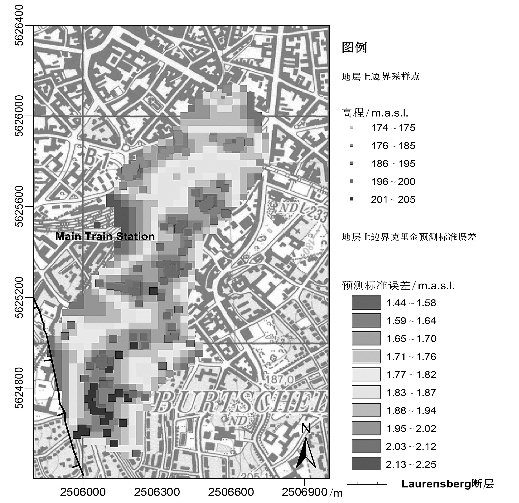
图5-22 主火车站地区的Hergenrath地层上边界克里金预测标准误差图
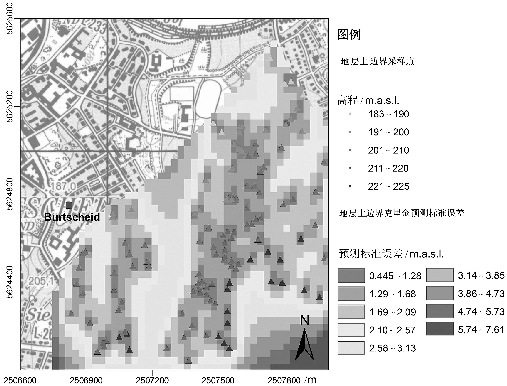
图5-23 Burtscheid地区的Hergenrath地层上边界克里金预测标准误差图
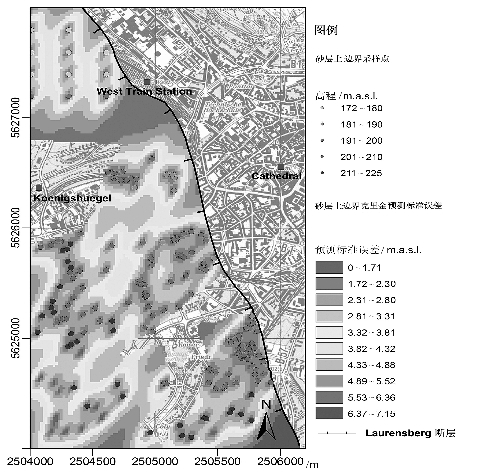
图5-24 Laurensberg断层上盘的Aachen砂层上边界克里金预测标准误差图
如图5-22至5-24所示,当估算位置更靠近采样点时,预测标准误差变小。在预测标准误差非常大的地区,也就是在采样点稀疏的地区,模型的用户可以决定是否需要添加新的测量数据来提高预测的精度。
5.1.6.2 地质条件复杂性和插值过程
克里金插值法有一个缺陷,就是预测过程具有平滑效应,即可能造成较小值被高估而较大值被低估的情况,不符合实际。使用密集计算方法可以克服克里金插值法的这一缺陷。利用密集计算法对模型进行多次计算,每次计算都从整体样本中随机抽取一组新的训练数据集。存储每次计算得到的模型,对每一个预测位置的多个预测值进行统计,用统计的标准偏差来表达该位置预测的不确定性。密集计算方法过程复杂,需要相当强的计算能力,目前很少应用于三维地质模型的评估(Culshaw,2005)。在本案例中,采用密集计算法来评估地质复杂性和预测过程带来的不确定性,步骤如下:
①对网格表面用于内插的钻孔数据重新进行采样;
②使用地质统计学方法对地质边界的高程值进行插值;(https://www.daowen.com)
③使用同样的插值网格,重复步骤①和②20次,记录每个网格中的预测值;
④对于每个网格,计算20次内插产生的预测值的标准偏差。
在统计学理论中,标准偏差公式为
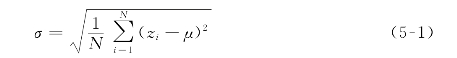
其中,σ是标准偏差,N= 20是重复插值次数,z i是每次插值得到的预测值,μ 是20次插值得到的平均高程值。
计算每个网格节点20次插值的标准偏差,结果如图5-25至5-27所示。
由图5-25至5-27可见,预测的标准偏差值非常小,均小于0.6。结果表明,在插值过程中所选择的变差函数模型基本可以反映样本的空间变异性。
由于空间信息化技术发展的局限和经费限制,在很多城市的地质数据库中,只存有钻孔记录或二维地质剖面图,只能传达特定的地质信息。地质数据的使用者可能并不具备专业的地质背景,很难通过一维或者二维的数据来估算地下条件,容易造成决策的偏差和失误。二维地质剖面图不能综合表达地下岩土体的几何属性和物理力学参数属性,从而限制了其在存在复杂浅层沉积物的城市环境中的使用。且在城市地质数据库中,数据格式多样、来源广泛,将多源异构数据综合到一个模型中,是城市地质工作的趋势。
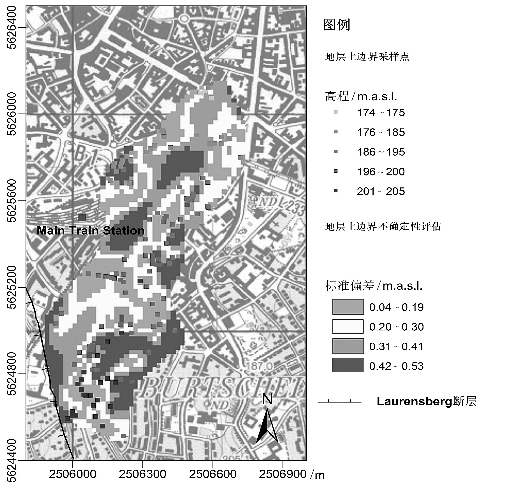
图5-25 主火车站地区的Hergenrath地层上边界由地质条件复杂性和插值过程引起的不确定性值

图5-26 Burtscheid地区的Hergenrath地层上边界由地质条件复杂性和插值过程引起的不确定性值
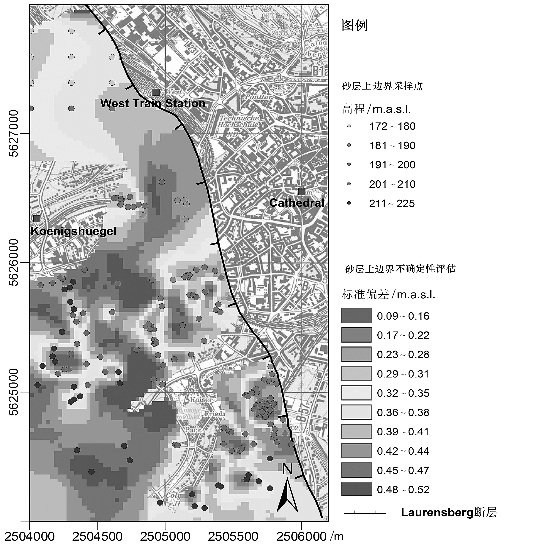
图5-27 Laurensberg断层上盘的Aachen砂层上边界由地质复杂性和插值过程引起的不确定性值
本案例构建的区域三维地质模型可以为进一步的岩土建模服务,应用场景如下。
(1)城市规划。所构建的三维地质模型可以离散为六面体元结构,每个体元中将存储地质、岩土、水文地质和不确定性属性参数,从而构成一个综合的城市三维地质和属性模型数据库,为城市规划服务。
(2)工程选址。在铁路或城市道路设施的建设中,沿着用户选择的路线切割模型很容易获得横截面。在剖面图中,可以展示每一个地质单元的地质信息和属性信息,从而为道路工程的选线提供详细的地下条件信息。对于重大基础设施建设,可在可行性研究和选址阶段提供精确度较高的地质框架和信息,从而找到符合经济性和安全性的场地。
(3)基础设施建设。针对某一具体的基础设施,可在三维地质模型中切割出工程场地模型,对该模型进行细化,构建详尽的三维属性参数模型,并将模型导入数值软件中,进行工程计算,全面服务工程建设。
