4.1.5 地质界面优化
在三维地层建模数据的插值技术中，克里金法虽然优于其他算法，但是它们都存在一个共同的缺陷，即插值后的层面与留作检验的控制点不完全吻合，插值曲面的部分区域并未完全落在控制点上。为了弥补这个缺陷，如第2.4节中介绍的，GOCAD 软件开发了针对地质建模特点的插值算法，即DSI。
4.1.5.1 问题的提出
如图4-10所示，S 为欧式空间上连续小面片或曲线多边形面元构成的曲面。设G= G（S）为多边形面元的边集合，Ω=Ω（S）为多边形面元的顶点集合，N=|Ω|为Ω 的点数，N（k）是k∈Ω 的邻域。
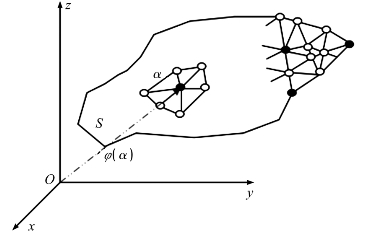
图4-10 离散光滑插值算法模型
设φ（k）是定义在所有节点k∈Ω 上的函数，并且仅在Ω 的子集上已知，则
由已知的φ（l）求未知的φ（i）的过程就是一种插值过程。
4.1.5.2 局部粗糙度准则
设R（φ| k）=
为定义在结点k 上的局部粗糙度准则，vα（k）为给定的权系数，可以为正、负、零，φ（α）为k的邻域上的点。
将局部粗糙度准则R（φ|k）代入全局粗糙度准则R（φ）=
其中μ（k）为给定的非负权函数，经过推导可以得出R（φ）可以完全由给定的值vα（k）和μ（k）确定。
令
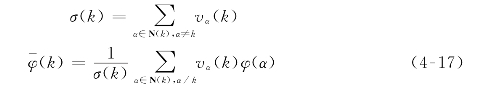
对局部粗糙度准则R（φ|k）进行变形，可以得出
从上式可以看出，R（φ|k）与|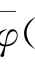
（k）-φ（k）|2成正比。
如果要使R（φ| k）=
=σ2（k）|¯φ（k）-φ（k）|2达到最小，就是使|¯φ（k）-φ（k）|2＜＜0，即使结点k 的值φ（k）趋近于其邻域点的平均值¯φ（k）。因此R（φ|k）越大，k 的邻域范围内的值越粗糙，反之越光滑，这就是局部粗糙度的物理意义。
4.1.5.3 提出约束条件
对于N 维行矩阵A i和一个常数b i定义的线性约束为
如果存在相同类型的几种约束条件，并用违反度来度量
其中，ωi为曲面S 上每个点的权重。则由N 维行矩阵A i所表示的线性约束可以表示为
4.1.5.4 线性约束解
DSI方程在上述线性约束下的解如下。
令R*（φ）= R（φ）+ρ（φ），该值越小，表明解的全局粗糙度越小，线性约束的违反度也越小，可以作为插值计算的目标函数。
将局部粗糙度与违反度函数代入，由
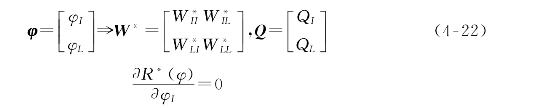
可得到DSI插值方程
因此，DSI插值方程的解，就是对目标函数进行二次求导得出的最小值。
实现上述过程需要如下三个步骤。
（1）对于一个给定控制节点集合，用DSI来生成和调整对应于地质体的初始界面（地质层位）。同样，用DSI来调整一个闭合多边形线，使其吻合到该线上的控制节点。
（2）多边形线上的每一节点被转变为一个对应于曲面S 的模糊控制点，并且插出牵引方向，沿着此线用DSI对其进行插值。
（3）使S 上的某些控制节点自由化，给曲面以更大灵活性，并且引入控制点的DSI插值。
DSI插值的自由性很好，在插值过程中能够对一些不确定的数据进行自动处理，在实际应用中有很大的灵活性。其在地质行业内拥有举足轻重的地位，已经成为多款软件的内核算法。
如图4-11所示，曲面插值后的区域中有部分层面未完全落在供校验的原始采样点（红圈内的三个点）上，即生成的地层层面与实际地层层面位置不吻合。因此需要使用DSI对地层层面进行光顺处理，其操作步骤如下。
（1）确定控制点（原始采样点），确定地层初始边界线。
（2）将地层界线转变为模糊控制点，并且引出插值方向。
（3）使用引入的模糊控制点在选定的插值方向上进行DSI插值，生成更加光顺的地层层面图。
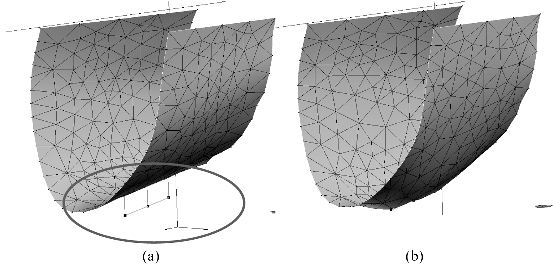
图4-11 经克里金插值后生成的层面（a）和DSI插值后层面（b）
图4-11（a）中，经克里金插值后，有三个原始采样点未落到曲面上。图4-11（b）中，经过DSI插值后的层面，所有的原始采样点都落于曲面上，表明经DSI处理后的地层层面与实际地层层面位置吻合较好。
由图4-11（a）和（b）的对比可以看出，在钻孔稀疏区用克里金法对原始采样点进行插值加密，再结合DSI插值对克里金插值产生的几何畸变进行修正后，生成的地层层面精度较高。
德洛奈三角剖分得到的三角形单元是平面的，DSI还可提高平面三角形的弯曲度，这更适合于描绘自然表面。除点约束条件之外，DSI还能够引入大量的线和面约束条件，将地质界面的粗糙度最小化，从而提高地质界面的质量。经过DSI优化后可以得到更平滑的表面，而无需考虑变量的空间变异性和预测误差的导数。因此，克里金插值法和DSI的组合是构建地质界面的一种实用而可靠的方法。