1.3.3 地杂波建模与抑制
地杂波是指气象雷达下视工作时,天线波束照射区内地面散射体的回波通过天线进入接收机而形成的一种地杂波。目前,利用统计模型仿真相关雷达杂波的方法,较有代表性的主要有球不变随机过程法(Spherieally Invariant Random Proeesses,SIRP)、无记忆非线性变换法(Zero Memory Nonlinearity,ZMNL)以及随机微分方程法(Stoehastic Differential Equations,SDE)[80-85]。SIRP模型属于外生模型(exogenous),能够独立控制序列的概率密度函数和协方差矩阵。在相关雷达杂波仿真中,可用SIRP法仿真相关瑞利、韦布尔和K分布地杂波。它的缺点是受所需仿真序列的阶数及自相关函数的限制,因此,当所需仿真序列较长时,计算负荷很大,不易形成快速算法。SIRP法在国内受到的关注不多,基本上停留在基本原理的理解上。ZMNL法可实现用于描述雷达地杂波的几种常用分布的仿真,但其应用受到功率谱形状等因素的制约。由于它易于实现且在相关高斯序列产生以后,速度较快,是目前在相关雷达杂波仿真中最引人注目的方法,并已得到广泛应用。国内也有关于ZMNL法应用的报道。SDE法没有SIRP法和ZMNL法流行[186-190],在国内少有人提及,国外对这一方面的研究也不多,且主要用于通信系统中干扰的仿真。根据SDE的理论,它可通过相关时间来控制序列的相关性,同样适用于相关雷达杂波的仿真。SDE法实际上是一个非线性自回归模型,具有产生速度相当快的优点,但这种方法对概率密度函数有一定的限制[191-200]。
由于地杂波大多是分布性的,具有大的体积,因此,对于气象雷达来说,在设计的时候必须充分考虑地杂波所带来的影响,并采取妥善的措施以保证气象雷达的性能。地杂波是一种连续分布杂波,它对机载雷达影响较大。由于遮蔽作用,并且可能存在偶然的强反射体,因此,地杂波的总体统计特性是非瑞利型的。这种情况下,对数正态分布和韦伯尔分布都获得广泛的应用。假若不考虑强反射体,那么在任何一个被雷达所照射到的距离单元内,地杂波振幅的统计特性往往是瑞利分布的。因此,一旦距离单元内的雷达平均截面积已知,地杂波模型便确定了。气象雷达的性能与非均匀地面杂波的特性密切相关。因此,在模拟时就有必要在地杂波模型中包含非均匀特性。对气象雷达而言,建立精确的地杂波的确定性模型必要性不大,可以建立一个假想的模型,该模型包含那些非均匀特性,并常采用对数正态分布函数来描述雷达截面积的空间起伏。国内外有大量有关后向散射特性的研究[80-82],许多研究部门根据各自的测试数据提出了很多散射系数与入射角的关系模型,比较有代表性的模型有现代雷达理论中普遍应用的常数γ模型、修正的地面散射模型等[83-85]。在雷达系统模拟中,可根据实际情况适当选取合适的散射模型。根据人们对地杂波统计特性的研究,地杂波的幅度分布特性可用一些数学模型来描述,最常见的有瑞利(Rayleigh)分布、对数正态(Lognormal)分布、韦伯尔(Weibull)分布以及K分布[86-89]。
地杂波是随机起伏信号,其功率谱特性可用功率谱密度或者自相关函数来表示。
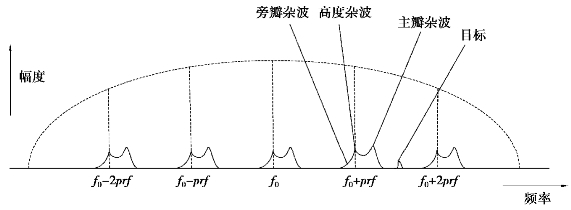
对于气象雷达,由于雷达处于运动平台上,地面上静止不动的景物相对于雷达有径向速度,再加上雷达波束指向以及雷达高速掠过的地形不断变化,地杂波的谱会显著变化,即使雷达高速掠过的是均匀平原地带也使机载雷达的杂波功率谱分布非常复杂。根据气象雷达地杂波的变化,通常将其分成主瓣杂波、旁瓣杂波与高度线杂波3部分。求解机载雷达地杂波功率谱的方法很多,如连续波近似法、H-R法[90-98]等。其地杂波功率谱示意图如图1.1所示。
 (https://www.daowen.com)
(https://www.daowen.com)
图1.1 机载雷达地杂波功率谱
对于地面固定的多普勒(PD)雷达而言,它的地杂波功率谱密度函数是处在发射信号频率上的单一谱线(经过距离门和窄带滤波后)。在PD雷达处于运动的情况下,如具有下视特点的机载PD雷达,当该雷达相对地面以速度VR运动时,杂波频谱就被这种相对运动速度所展宽,并且多普勒频谱的范围处在相应于雷达运动速度的多普勒频率的正边和负边。
气象雷达地杂波模型从系统仿真角度来分主要有地杂波功率模型和相干地杂波模型两种,地杂波功率模型是对杂波平均功率的一种描述。该模型实现的基础是雷达距离方程,进一步由信杂比、目标和杂波的统计特性可得出雷达目标发现概率或虚警概率,它对系统大规模的仿真和某些实时仿真用途较大,但这种模型被雷达和地面的几何关系限制,不能仿真实际气象雷达要进行的整个检测过程,相干地杂波模型利用了地杂波的相位,包含了有关雷达环境的全部信息,比前者复杂得多,实现较为困难,但是因为它能仿真实际雷达要进行的整个检测过程,因此相干地杂波模型是雷达信号级仿真所必需的,机载雷达杂波模型有不少文献研究过[116-126],但任意姿态下的机载雷达地杂波模型却很少提及。雷达地杂波的研究经过长期发展,目前常用的地杂波模型有3种:第一,描述地杂波的幅度统计分布模型和杂波功率谱的统计模型,目前应用较广的有对数正态分布、韦伯分布和K分布[201-210]。第二,描述地杂波散射单元的机理模型,属于地杂波雷达截面积的理论分析范畴,如组合表面模型,但一般只针对特定地貌。第三,描述地杂波后向散射系数与雷达工作频率、极化和环境参数等相关物理量依赖关系的模型,主要有常数γ模型,用于气象雷达下视情形,描述了后向散射系数与角度的关系。
根据机载气象地杂波的特点,最初的地杂波抑制技术是针对地杂波多普勒频移和频谱展宽分别进行的。补偿地杂波多普勒频移的主要方法是杂波锁定,其典型代表是时间平均相干机载雷达技术(TACCAR)和自适应AMTI技术[210-215]。TACCAR是麻省理工学院;林肯实验室提出的杂波多普勒频移补偿方法。它通过对一段距离在几个脉冲重复周期的回波采样测得杂波的平均中心频率,并采样锁相环控制相干振荡器频率,这样回波的多普勒频移被消除。TACCAR的缺点是其测得的是杂波平均多普勒频率,而机载雷达各距离单元的多普勒频移是不同的。因此,为了取得更好的效果,需要多个杂波测量和跟踪系统,以对应不同的距离单元。由于机载雷达杂波频谱具有很强的空时耦合性,空时二维联合处理将取得很好的杂波抑制性能。L.E.Brennan于1973年提出了空时二维自适应处理(STAP),并导出了最佳处理器结构。为了补偿机载雷达平台运动引起的杂波多普勒频谱展宽,F.R.Dickey和D.B.Anderson等人提出了相位中心偏置天线(DPCA)方法。对气象雷达地杂波的抑制,目前国内多采用自适应滤波算法和非相参MTI对消器,其中自适应预测误差滤波器的频率响应为输入杂波功率谱的倒置,频率响应能够随着地杂波的变化改变。自适应算法分为两类:一类以最小均方误差为准则,另一类以最小二乘误差为准则[215-223]。n次对消器的基本实现是通过一定的延迟手段使n个连续回波脉冲信号延迟加权相加。通过比较不同阶次的频响特性和抑制效果,可选择最适合滤除地杂波同时又保持目标信号的n值。
国内一些高校和研究院所对气象雷达的地杂波建模与抑制方面也多了很多的研究工作,如电子科技大学、西安电子科技大学、中电十所等。例如,电子科技大学对DPCA方法作了多年的研究,并将DPCA杂波补偿方法应用于某型机载雷达的主杂波抑制系统中,取得了较好的效果,西安电子科技大学重点研究了STAP及其简化,取得了丰硕的成果,并相继提出了一系列STAP简化算法和实用处理机构。此外,清华大学、中电十四所也做了大量的地杂波建模与抑制方面的工作。
