2.1.3　雨回波

2.1.3　雨回波

雨是从云中降落的水滴，陆地和海洋表面的水蒸发变成水蒸气，水蒸气上升到一定高度之后遇冷变成小水滴，这些小水滴组成了云，它们在云里互相碰撞，合并成大水滴，当它大到空气托不住的时候，就从云中落了下来，形成了雨。

雷雨和阵雨是雨的两种主要形式。雷雨、阵雨回波多出现在冷锋和冷涡天气系统中，由于雷雨、阵雨都是对流降水，因此，它们都具有对流云降水回波的特征。正确区分是雷雨还是阵雨是十分重要的。大致有以下5类：

①回波外形：阵雨块状比雷雨小，阵雨体积一般水平尺度在10km以下，而雷雨单体水平尺度在10km以上，阵雨单体显得干瘪，边缘比较清楚、平滑。雷雨单体表现得肥厚，结构密实，边缘起伏曲折，且边缘略发毛。

②回波高度：在RHI上阵雨高度较低，一般在8～9km以下。雷雨回波高度则常在10km以上。雷雨单体顶部常呈花椰菜。雷雨总体回波粗壮如树，阵雨则常细小如针。

③回波强度：雷雨回波比阵雨回波强，雷雨中可能伴有冰雹，阵雨里无雹。

④反射率因子：雷雨回波通常在40dB以上，而阵雨回波常常不到40dB。

⑤径向速度场特征：阵雨回波由于水平尺度小，探测资料已证实单体内存在正或负径向速度，而雷雨回波单体大，回波强，单体内常同时存在正、负径向速度，存在风向风速的切变。

当雨回波体积内存在大量各种直径的降水粒子时，假定粒子间的间隔大于几个气象雷达的波长以上；而且粒子以某一速度移动的距离相对于波长可以充分长。设由径向速度分量为vr到vr＋dvr之间的粒子接收到的功率P为

式中，G（vr）为多普勒速度谱。

由于粒子径向速度λ与多普勒频率fd之间有

则式（2.16）中dP用功率谱密度G（f）来表示为

式中，df是与dvr相应的频率区间，将上式在全频域或全部速度范围内积分，得总的接收功率Pt为

式（2.19）表明，只要将回波多普勒频谱图横轴的频率换算为速度，则该频谱曲线的形状就完全表示了目标体积内粒子的速度分布。求得回波多普勒频谱，就可求出目标体积内粒子径向速度的分布。

气象雷达主要处理降水粒子的回波，雨回波的功率谱，应该分布在发射频率f0附近，如图2.5所示。

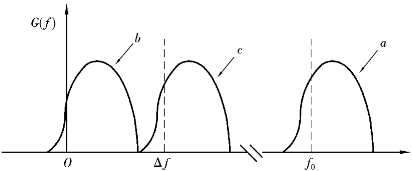
图2.5　雨回波功率谱

如图2.5所示的曲线a，G（f）为功率谱密度。相干检波后信号的功率谱相对于图2.5中将纵轴移到f0处，即得图2.5中的曲线b，分布在零频附近。当目标体积内包含有正负速度的粒子时，将发生频谱的重叠，为了避免这种重叠，用f0－Δf代替f0作基准频率相干检波。使多普勒频谱移到图2.5中曲线c的Δf附近，Δf称作补偿频率。把Δf代入fd＝2vr/λ求得的补偿速度Δv。此外，还可将接收信号与两个相位差为90°的基准信号作正交相位检波，由得到I，Q两路信号输出进行运算分别取出正负速度。

下面对降水回波信号进行分析。在发射连续波的情况下，在天线端口接收到的回波电压为［100-105］：

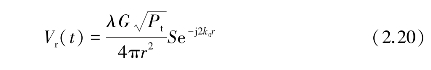
式中，S是球形粒子的散射矩阵元素。如图2.6所示的几何图，将r与t的函数关系表示为r（t）。设发射信号为str（t）＝Utr（t）ej2πf0t，则回波信号sr（t）就可写为

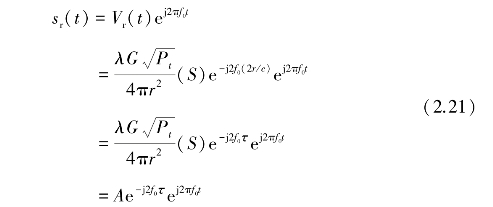
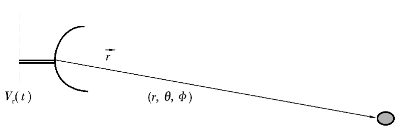
图2.6　球形微粒的运动

其中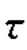，＝2r/c，k0＝2π/λ＝2πf0/c，c为光速。为了方便，因子λG（S）/4πr2用幅值A表示，则sr（t）可简化为

图2.6中，位于r→处的单个球形微粒，向量r→的起点在雷达处，随着球体的运动，距离r和Vr的相位2k0r均随时间变化。注意：k0＝2π/λ。

当发射信号为频率f0的连续波时，即str（t）＝exp（j2πf0t），式（2.48）可写为

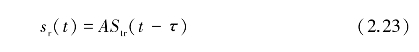
而exp（－j2πf0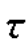）可写为

r随t变化必然导致上式中的θ也随t变化。故粒子散射波的相位θ随粒子相对于雷达的运动而变化，并且θ的时间变化率与多普勒频移有关。

令发射信号具有一般形式str（t）＝Utr（t）exp（j2πf0t）。根据式（2.24），回波信号sr（t）可写为

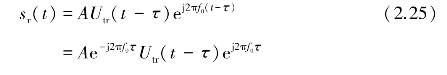
则回波信号的电压为

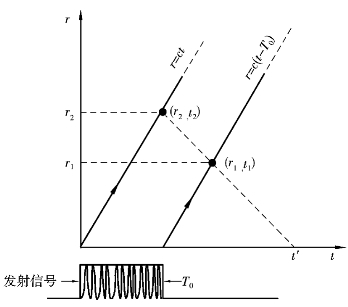
图2.7　理想情形下两个粒子的散射示意图

　　一般来说，散射幅度是时变的，其函数关系可写为A（t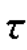，）。假设在理想条件下，距离雷达r1，r2处有两个粒子，它们的散射幅度是时变的，如图2.7所示。在水平时间轴下面画出了宽度为T0的矩形发射波形。注意：图2.7中的纵坐标表示径向距离。发射脉冲前沿的传播路径用特征直线r＝ct表示，后沿的传播路径用特征直线r＝c（t－T0）表示。两粒子的反射信号同时到达雷达的时刻t′，可根据斜率为－c的特征直线确定，即直线r－r1＝－c（t－t1），如图2.7所示。在该坐标系中，两个粒子的坐标分别为（r1，t1）和（r2，t2）。因此，t′时刻到达雷达的反射信号是距离r2和r1处两个粒子回波的合成。其中，r2处粒子的散射幅度在t2＝t′－r2/c时刻确定；r1处粒子的散射幅度在t1＝t′－r1/c时刻确定。因此，反射信号幅度的基本形式就是A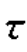（；t）或A（r；t），其中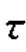，＝2r/c确定延时时间。

一般来说，降水由大量的水凝物组成，这些水凝物分布在很大的空间距离上，它们的散射幅度和运动速度也各不相同。现在假设回波电压是由区间r到r＋Δr（或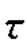＋Δ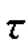）内的粒子散射，如图2.8所示。对应的宽度为T0的矩形发射脉冲的距离-时间图，如图2.9所示。定义A′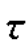（；t）为Δ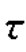单位距离增量（或Δr）内粒子的散射幅度。根据式（2.52）就可以得到相应的回波电压增量为

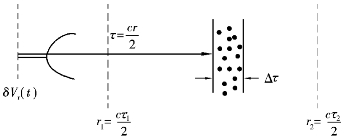
图2.8　在区间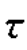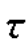（，＋Δ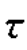）内粒子散射的回波电压增量示意图

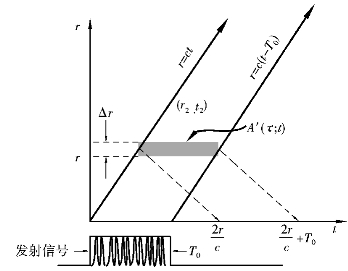
图2.9　分布在（r，r＋Δr）区间内粒子示意图

若散射介质的距离范围为r1到r2，则有

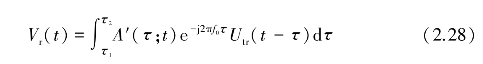
从形式上，上式的积分限可扩展为0到∞，因此，对于任意形状的发射波形（不一定是矩形脉冲）。其回波电压的一般形式为

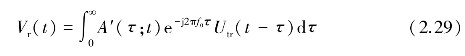
在图2.10中，粒子的“瞬时”位置由相对于雷达的矢量序列rk（k＝1，2，…）表示。相角θk＝2πf0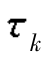＝（4π/λ）rk。对于随机分布的粒子，相角θk在（－π，π）间均匀分布。通常散射幅度Ak的函数形式为Ak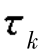（；t）。

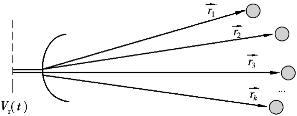
图2.10　随机粒子集合的示意图

根据式（2.29），回波电压同样可表示为介质中单个散射粒子作用的回波电压之和的离散形式，即

其中，Ak为第k个粒子的散射幅度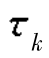，＝2rk/c。

在图2.11中，假设相角θk在（－π，π）间均匀分布，可把合成的相位矢量表示成I＋jQ。其中，I为同向分量，Q为正交分量。对于任意给定频率，给定时刻t的Vr（t）可以表示为它的所有相位矢量元素求和的形式。

考虑Vr（t＋Δt），在Δt时间内，rk（或者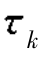＝2rk/c，θk＝（4π/λ）rk）会随着粒子的运动而变化。如果Δt很小，那么，t和t＋Δt时刻合成的相位矢量近似平行；随着Δt增大，合成的相位矢量不再平行；当Δt足够大时，Δrk相当于波长的很大一部分，这就导致Vr（t＋Δt）与Vr（t）不相关。

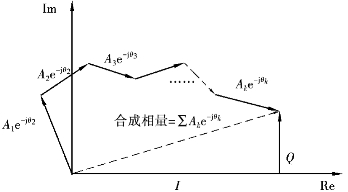
图2.11　复平面上的相位矢量合成