4.2.2 湍流散射
2026年01月15日
4.2.2 湍流散射
大气中总是存在着各种尺度的湍涡,随着高度的升高,大尺度的湍涡所占比例越来越大。各种尺度的湍涡在传输过程中都会逐级破碎,能量无衰减地逐级传输直到最小尺度,最后耗散为分子热运动能量。
由于大气中温度、压力、湿度分布不均匀,致使各湍流微团的大气折算率有所差异,大气折射率结构常数分布不均匀。当雷达电磁波入射到不同湍流微团界面时,这种折射指数的不均匀结构将对电磁波造成散射。
根据麦克斯韦方程组的积分形式,有计算式子[180-182]
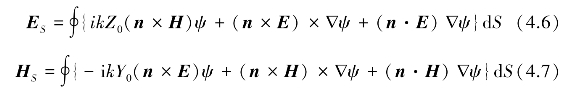
式中,n是表面元dS的单位法向矢量,格林函数ψ为
![]()
式(4.8)中的距离r是从表面元dS至所需散射场点(可能是另一个表面元)的距离值。这些表达式表明,如果在一个完全闭合面S上总的电场和磁场分布已知。那么,空间上任何一处的场都可通过在整个表面上求这些表面积分来计算。
用小扰动法对均匀各向同性的折射率起伏场,求取与入射电矢量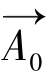 成θ角的散射方向
成θ角的散射方向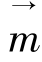 的散射平均强度
的散射平均强度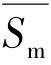 为[101-105]
为[101-105]
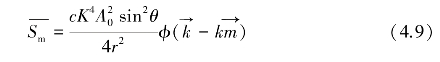 (https://www.daowen.com)
(https://www.daowen.com)
式中,![]() 表示(k-km)尺度的湍流能量的谱密度。
表示(k-km)尺度的湍流能量的谱密度。
当散射体积V为无限时,与此波段(k-km)相对应的折射率不均匀尺度为
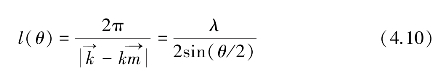
当散射体积V为有限时(线性尺度为H),对θ方向散射有贡献的谱分量包含在下列尺度区间内
![]()
在实际的湍流探测中,电磁波波长λ总是远小于散射体尺度H,则式(4.10)和式(4.11)比较接近,即对于给定的角度θ上的散射,只取决于折射率不均匀性的一个狭窄谱段。
对于后向散射θ=π,则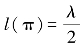 ,即有效的湍流尺度为气象雷达波长的1/2。
,即有效的湍流尺度为气象雷达波长的1/2。
对于均匀湍流场,利用折射率结构常数,可导出湍流介质对波长λ的电磁波反射率为[101-105]
![]()
