4.2.1　湍流尺度与相关系数

4.2.1　湍流尺度与相关系数

研究湍流时，通常采用湍流脉动量。某个物理量的湍流脉动量是指该物理量与其平均值之差，即u′＝u（t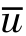）－。流体作湍流运动，由于不规则脉动引起动量输送所产生的流体内部的相互作用力，称为湍流黏性应力（也称雷诺应力）。在（x，y，z）坐标系中，任一点的雷诺应力有9个分量，组成二阶对称张量，以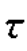表示为［101-105］

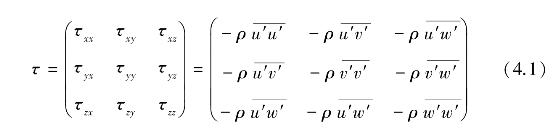
式中，u′，v′，w′为湍流在3个坐标方向的流速脉动量，ρ为流体密度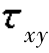，表示与x轴垂直的（y，z）平面上的湍流应力在y方向的分量，其他类同。

湍流相关系数是用来表征湍流场两个脉动变量相关程度的数学表达式。如，速度方向相同称为自相关，速度方向不同称为互相关。相关系数反映湍流尺度的大小。湍流尺度大，则两点容易落入同一个湍涡中，相关系数大。小尺度湍流，总使得u′（x1）与u′（x1＋x）不相关，则相关系数小。湍流尺度是指湍涡的平均尺度。设湍流相关系数为f（x），则湍涡平均尺度可表示为

在湍流场的探测和研究上主要有两种方法，即固定空间点的欧拉法和固定湍流微团的拉格朗日法，则欧拉空间自相关系数［101-105］

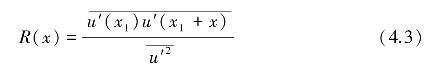
欧拉时间相关系数和拉格朗日相关系数分别为［101-105］

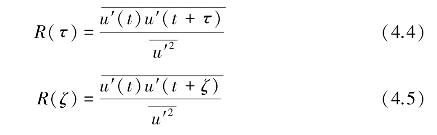
根据泰勒“冰冻”湍流假设（湍流是“冰冻”成一固定形式，以一定的平均速度u移动，某点A涨落的时间变化是“冰冻”湍流通过A点引起的），空间中固定点的随时间变化和给定时间的空间变化是相同的。因此在实际应用中，常假设欧拉时间相关系数与拉格朗日相关系数的函数形式相同，只差一个比例参数。