5.4.4 地杂波抑制滤波效果对比
本节给出传统杂波滤波方法和LMS-ANC和LSL-ANC滤波方法在一个扇面所有扫描线上的信号滤波后,其风速估计误差、信杂比改善的对比;并给出它们对一条扫描线滤波所需的平均运算时间对比。
(1)风速误差对比
1)一个扇面所有扫描线上的风速相对误差均值对比
为了对比LMS-ANC和LSL-ANC两种滤波方法对一个扇面所有扫描线上的雷达回波信号滤波后,计算得到的风速估值相对雨回波风速估值的情况,图5.26给出所有扫描线上分别经过两种滤波方法滤波后得到的风速相对误差均值。第j条扫描线上滤波后雷达回波信号的风速相对误差均值定义为第j条扫描线上滤波后雷达回波信号的风速误差绝对值的均值与第j条扫描线上雨回波的风速估值的比值
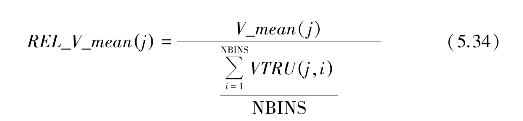
式中,REL_V_mean j()表示第j条扫描线上雷达回波信号的风速相对误差均值,其余参数见式(5.28)—式(5.30)中的定义。
图5.26中,“LMS误差”和“LSL误差”分别表示经过LMS-ANC,LSLANC滤波后雷达回波信号的风速相对误差均值;MTI1,MTI2分别表示经过一次MTI相消器、二次MTI相消器滤波后雷达回波信号的风速相对误差均值。
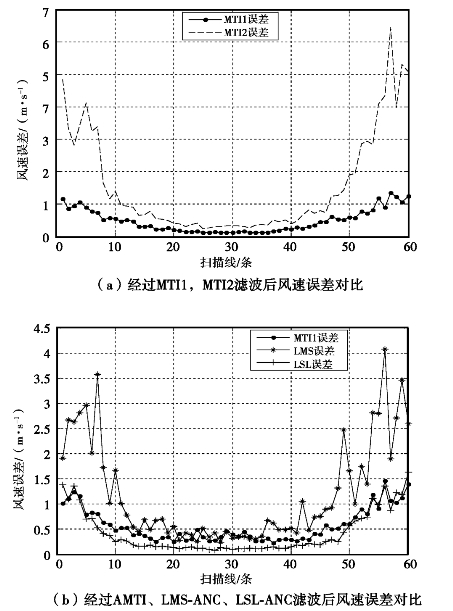
图5.26 经过各种滤波方法后的风速相对误差均值对比
由图5.26可知,从整体上看,经过LMS-ANC和LSL-ANC滤波后,雷达回波信号的风速估值相对误差在中间扫描线处较小而在两边扫描线处较大,这说明在中间扫描线处,滤波后雷达回波信号的风速估值相对接近雨回波风速估值,即在中间扫描线处的风速估值较好;且“LSL误差”<“LMS误差”。
2)整个扇面上风速绝对误差均值对比
下面定义一个扇面上的风速估值与雨回波风速估值的绝对误差均值为
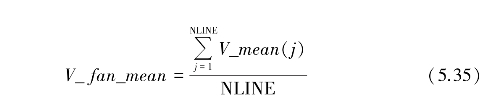
一个扇面上的风速估值与雨回波风速估值的绝对误差的标准差定义为
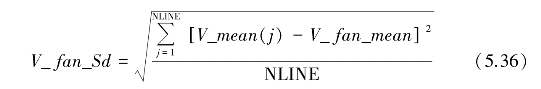
上面两式中所用到的参数见式(5.33)中的定义。
根据式(5.35)、式(5.36)中的定义,表5.7给出了一个扇面上的雷达回波信号分别经过LMS-ANC,LSL-ANC滤波后的风速误差均值及标准差,表中按照风速误差均值从小到大的顺序将LMS-ANC,LSL-ANC滤波方法与传统的滤波方法进行了排列。
表5.7 风速误差对比
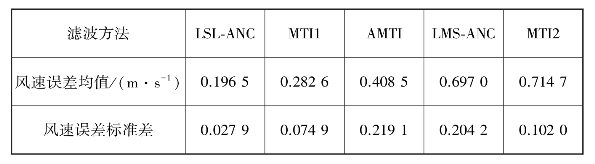
对比图5.26与表5.7可知,图5.26与表5.7对应一致,且一个扇面的雷达回波信号分别经过LSL-ANC,LMS-ANC滤波后,其风速误差均值依次增大。以风速误差为对比参数时,LSL-ANC方法最优。
(2)信杂比对比
1)一个扇面所有扫描线上的信杂比对比
图5.27给出所有扫描线上滤波前信杂比以及分别经过LMS-ANC,LSL-ANC两种滤波方法滤波后雷达回波信号的信杂比;图5.27中,“SCR”表示滤波前雷达回波信号的信杂比,“SCR-LMS”和“SCR-LSL”分别表示LMS-ANC,LSL-ANC滤波后的雷达回波信号的信杂比。(https://www.daowen.com)
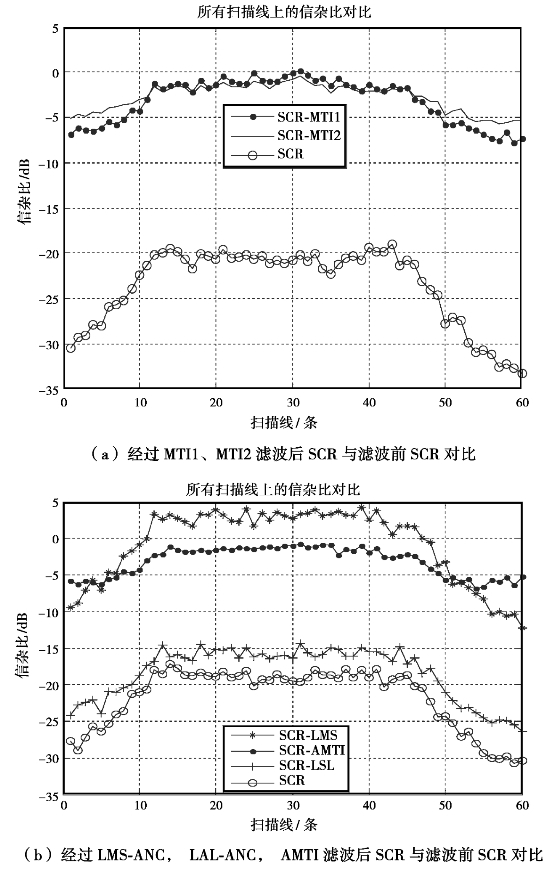
图5.27 滤波前信杂比及分别经过各种滤波方法后的信杂比对比
由图5.27可知,经过不同滤波方法滤波后,“SCR-LMS”>“SCR-LSL”,且滤波后雷达回波信号的信杂比均远大于滤波前的雷达回波信号的信杂比。可见,以信杂比为对比参数时,LMS-ANC方法要优于传统的AMTI方法;同时也优于LSL-ANC方法。
2)整个扇面上信杂比均值对比
此处定义一个扇面上的信杂比均值为
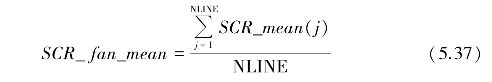
定义一个扇面上的信杂比标准差为
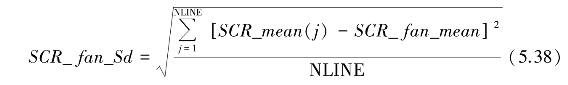
上面两式中用到的参数见式(5.25)—式(5.27)中的定义。
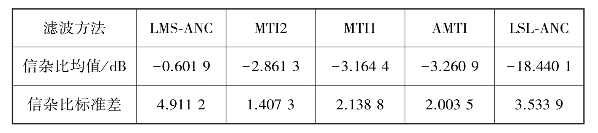
根据式(5.37)、式(5.38)的定义,表5.8给出了一个扇面上的雷达回波信号分别经过LMS-ANC,LSL-ANC滤波后的信杂比均值和信杂比标准差。表中按照信杂比均值从大到小的顺序将各种滤波方法进行排列。另外,滤波前信杂比均值和标准差分别为-21.859 7dB和4.196 9。
结合图5.27和表5.8可知,图5.27和表5.8对应一致,且一个扇面的雷达回波信号分别经过LMS-ANC,LSL-ANC滤波后,其信杂比均值依次减小。可见,以信杂比为对比参数时,LMS-ANC方法最优。同时,通过表5.8可以看出,采用LMS-ANC,LSL-ANC滤波后其信杂比得到了很大提高,且信杂比标准差均小于滤波前的信杂比标准差。
表5.8 信杂比对比
(3)运算时间对比
经过不同滤波方法的运算时间(对一条扫描线滤波所需的平均运算时间)如图5.28所示。
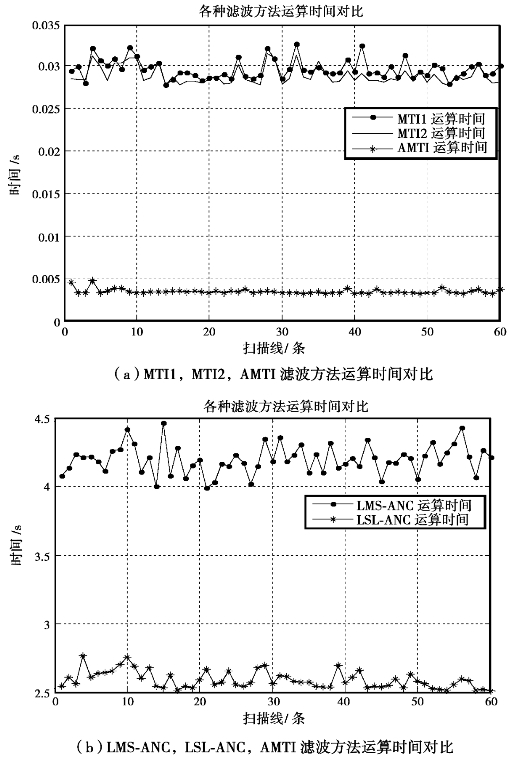
图5.28 经过各种滤波方法的运算时间对比
在相同的计算机仿真环境下,不同滤波方法对每条扫描线上的信号进行滤波所需的平均运算时间见表5.9。
表5.9 运算时间对比

由表5.9可知,传统的AMTI,MTI滤波方法的运算时间要小于LSL-ANC和LMS-ANC方法;同时,LMS-ANC的运算时间要长于LSL-ANC滤波方法所需的运算时间,这是由于LSL-ANC算法本身的运算造成的时间较长,而LMS-ANC是由于在算法运算中,对步长μn(0<μn<1/λmax)和参数β(0<β<1/λmax)的取值范围进行限制造成的:限定其取值范围需计算λmax,计算λmax需对输入序列的自相关矩阵进行计算,而该过程花费时间较长。可见,以运算时间为对比参数时,LSL-ANC方法要优于LMS-ANC方法。
上面给出了LMS-ANC,LSL-ANC两种滤波方法滤波后的雷达信号的风速误差对比、信杂比对比和滤波所需的运算时间对比。由对比可知,LMS-ANC,LSL-ANC滤波方法在不同的对比标准下,其性能好坏不同:以风速误差、运算时间为对比参数,LMS-ANC,LSL-ANC滤波方法要优于传统的MTI,AMTI滤波方法;但以运算时间为对比参数时,LMS-ANC,LSLANC两种滤波方法的运算时间要大于传统的MTI,AMTI滤波方法。在实际应用中,可根据实际情况选择。而运算时间的考虑可根据所用硬件的运算速度来定。
