5.4.1 传统地杂波抑制方法
（1）MTI方法
传统的地杂波抑制方法主要有动目标显示（Moving Target Indicator，MTI）和自适应动目标显示（Adaptive Moving Target Indicator，AMTI）滤波方法。
常见的MTI滤波器是一种n次相消器，它的基本实现是通过一定的延迟手段（模拟的延迟线或数字信号存储部件等）使n个连续回波脉冲信号延迟加权相加［1 80－18 2］。它又分为非递归型和递归型两种。非递归滤波器的频率响应较差，要获得较好的响应就必须增加足够多的延迟部件和处理更多的脉冲信号，带来的缺陷是滤波器的组成复杂和处理快速运动目标能力不足。
n次相消器的缺点：只能抑制固定地杂波（低频端），无法抑制运动地杂波。为了克服这个不足，又提出了抑制运动地杂波滤波器，使滤波器频率响应特性的“凹口”对准杂波的平均多普勒频率，达到抑制运动杂波的目的。其主要缺点是当背景环境中存在分布在频谱的多个不相邻位置的运动杂波时，滤波器的权值调整将会变得非常麻烦，并且滤波器的结构复杂度也会迅速增加。
一次MTI相消器的频率响应为
二次MTI相消器的频率响应为
一次相消器和二次相消器的结构框图分别如图5.8和图5.9所示。
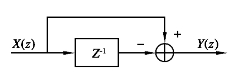
图5.8 一次相消器结构
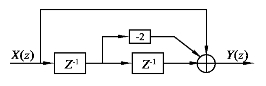
图5.9 二次相消器结构
一次相消器的幅度多普勒速度特性如图5.10所示。由图5.10可知，其通带临界速度约为15.027 1m/s，阻带临界速度设为3m/s，因此，其过渡带宽度约为12m/s。二次相消器的幅度多普勒速度响应如图5.11所示。由图5.11可知，其通带临界速度约为19.103m/s，若阻带临界速度设为3m/s，因此，其过渡带宽度约为16m/s。由上述可知，一次相消器和二次相消器的过渡带均太缓，因此，若使用其滤除地杂波，易造成气象目标回波损失，且二次相消器将对10m/s内的回波衰减更大。
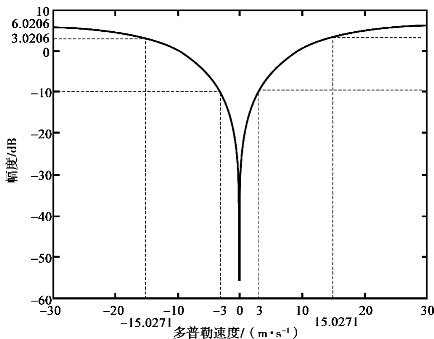
图5.10 一次相消器的幅度-多普勒速度响应
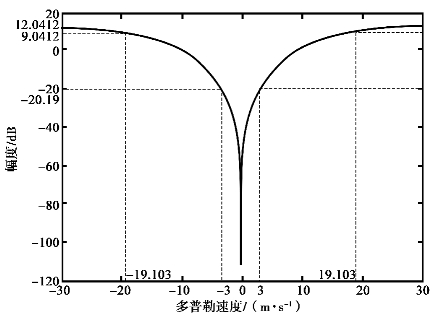
图5.11 二次相消器的幅度-多普勒速度响应
经过一次MTI相消器滤波后雷达回波信号的多普勒谱三维图和二维俯视图分别如图5.12（a）、（b）所示；图5.12（c）给出了地杂波和雨回波均较强的距离门范围（20～38个距离门）内的滤波前、后的信杂比对比；滤波后雷达回波信号的风速估值与雨回波风速估值的对比如图5.12（d）所示。
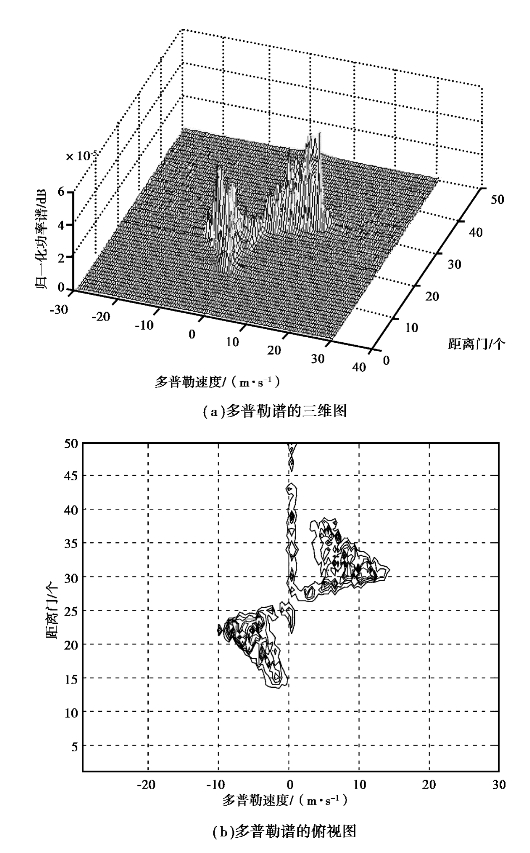
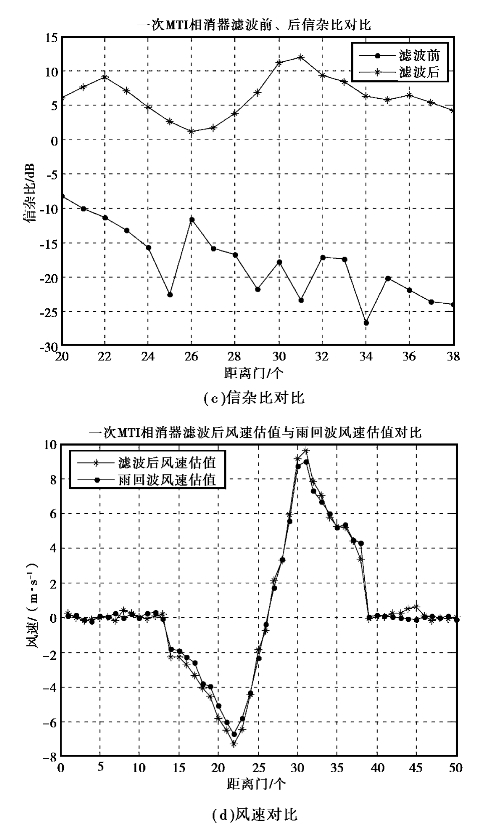
图5.12 一次相消器滤波后雷达信号的多普勒谱、信杂比对比及风速对比
图5.12（a）、（b）分别给出了滤波后雷达回波信号的多普勒谱三维图和二维俯视图，由其可以清楚看出在距离门22～30发生了较强的风切变；第25～50个距离门处仍存在较强的零多普勒速度地杂波，这是由于在该距离门范围内，滤波前雷达回波信号中的地杂波较强，而一次相消器的阻带衰减较小，使得杂波未滤除干净；在1～24个距离门处，由于滤波前杂波在该范围内的强度较小，因此经过滤波后，该距离范围内的地杂波几乎被完全滤除；且零多普勒速度附近的雨回波和地杂波一起得到了抑制，但由于该相消器的阻带衰减较小，雨回波的衰减程度也较小，又由于该相消器的过渡带较宽，因此较宽多普勒速度范围的雨回波被抑制。
由图5.12（c）可知，在地杂波和雨回波均较强的距离门范围（20～38个距离门）内，滤波后的雷达回波信号的信杂比与滤波前相比提高14～36dB。
由图5.12（d）可知，经过一次MTI相消器滤波后雷达回波信号的风速估值与雨回波风速估值接近。
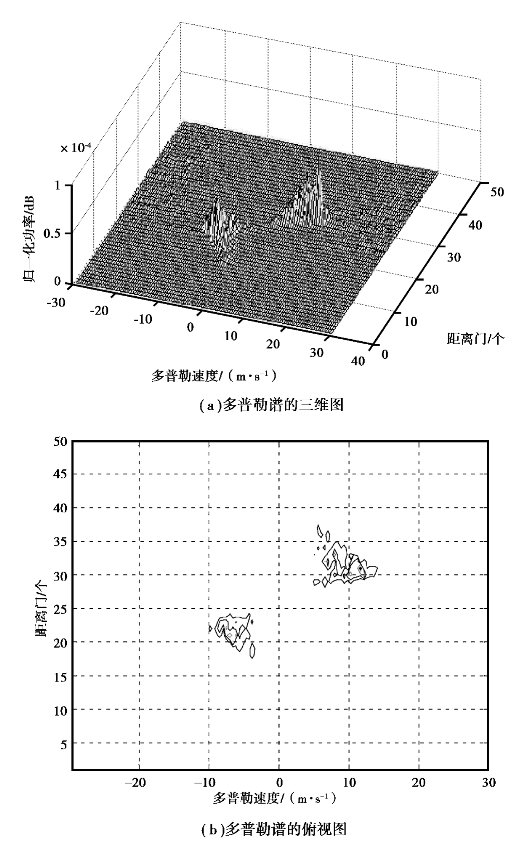
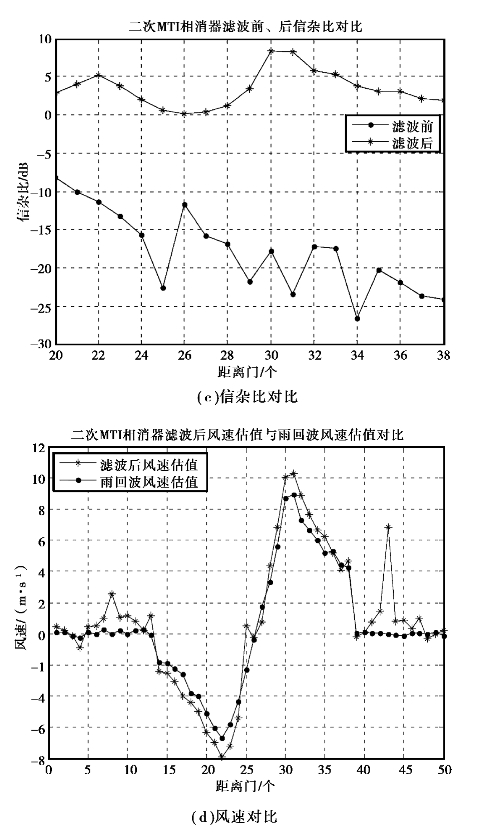
经过二次MTI相消器滤波后雷达回波信号的多普勒谱三维图和二维俯视图如图5.13（a）、（b）所示；图5.13（c）给出了地杂波和雨回波均较强的距离门范围（20～38个距离门）内的滤波前、后的信杂比对比；滤波后雷达回波信号的风速估值与雨回波风速估值的对比如图5.13（d）所示。
图5.13（a）、（b）分别给出了滤波后雷达回波信号的多普勒谱三维图和二维俯视图，由其可以清楚看出在距离门22～30发生了较强的风切变；从图5.13（b）可以看出，经过二次MTI相消器，地杂波大部分被滤除，同时雨回波也得到明显抑制，这是由滤波器阶数越高阻带衰减越大且二次相消器的过渡带较宽导致的，这与上面对二次相消器的分析一致。
由图5.13（c）可知，在地杂波和雨回波均较强的距离门范围（20～38个距离门）内，滤波后的雷达回波信号的信杂比与滤波前相比提高12～33dB。
由图5.13（d）可知，经过二次MTI相消器滤波后雷达回波信号的风速估值与雨回波风速估值相接近，但其接近程度小于一次MTI相消器滤波后的雷达回波信号的风速估值与雨回波风速估值的接近程度。
图5.13 二次相消器滤波后雷达信号的多普勒谱、信杂比对比及风速对比
（2）AMTI方法
AMTI（Adaptive Moving Target Indicator）技术［18 2］是传统固定MTI的改进，它可自适应地调整MTI滤波器的凹口位置和宽度。由于平台的运动使杂波谱平移和展宽，在这种情况下，地杂波经固定MTI后仍会余留一部分，有时甚至难以对消。余留的地杂波并不能通过增加MTI的级数来大幅度消除，而只能靠自适应的偏移MTI滤波器的凹口和改变凹口宽度来实现。
可用如图5.14所示的矢量图说明一阶AMTI的工作原理。一阶AMTI系统框图如图5.15所示。其中，φ是由于平台运动所带来的相位超前φ＝2πfdTr，X（t），X（t－Tr）分别为t，t－Tr时刻的回波，Tr是雷达脉冲重复周期。
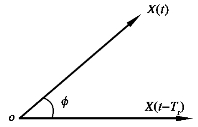
图5.14 AMTI矢量图［53］
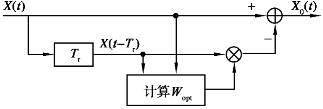
图5.15 一阶AMTI系统框图［53］
为了达到对消地杂波的目的，将X（t－Tr）乘以因子Wopt＝rejφ，这样X（t），X（t－Tr）就处于同一方向上，消除了由于平台运动而带来的相位变化，可以直接进行对消。若用X［n］代替X（t），X［n－1］代替X（t－Tr），由图5.15可得输出X0［n］为
其传输函数为
将Wopt＝rejφ代入式（5.20），则有
可见，该系统在f＝（φ/2π）×fr＋nfr（n为整数）处有凹口，达到了移动滤波器凹口的目的。权的模r决定滤波器凹口的宽度，随着r的增大，凹口变窄。
滤波器凹口移动位置和凹口宽度变化取决于权Wopt。在机载雷达系统下视扫描方式时，地杂波相当强，因此只要保证滤波器输出功率最小，就能最大程度的抑制地杂波，所以采用最小输出功率准则确定Wopt，可推导出Wopt为［53，182］
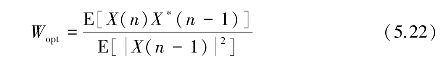
实际应用中，自适应权值Wopt可近似计算为［53］
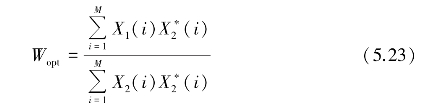
式中，X1为X［n］所组成的矢量，X2为X［n－1］所组成的矢量。
对回波中所包含的运动目标信息S（n），由于它所对应的多普勒频移与大面积杂波的多普勒频移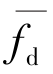
存在着差别，所以S（n）与Wopt×S（n－1）在方向上不重合，故AMTI技术能消除地杂波，保留运动目标信息。要想获得更优的性能，可采用高阶AMTI。
利用AMTI方法抑制地杂波后雷达信号的多普勒谱、滤波前后信杂比对比及滤波后风速估值与雨回波风速估值的对比如图5.16所示。
利用AMTI方法抑制地杂波后雷达回波信号的多普勒谱如图5.16（a）、（b）所示；图5.16（c）给出了地杂波和雨回波均较强的距离门范围（20～38个距离门）内的滤波前、后的信杂比对比；滤波后雷达回波信号的风速估值与雨回波风速估值的对比如图5.16（d）所示。
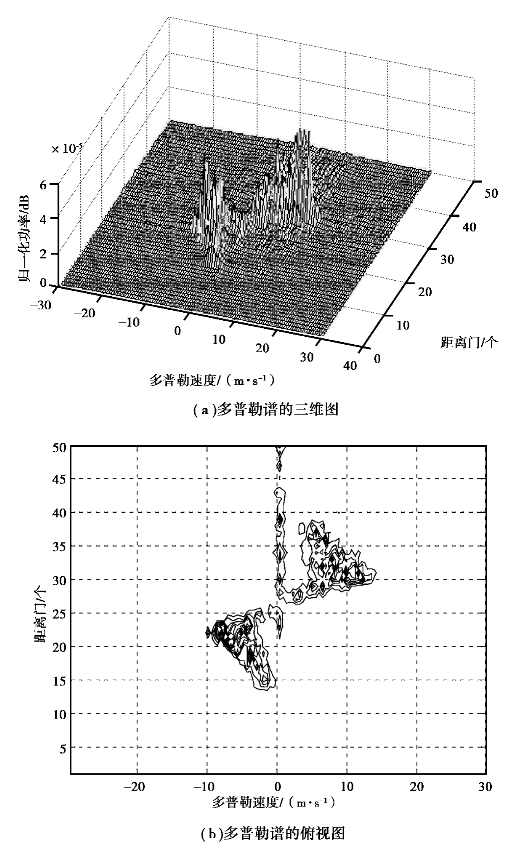
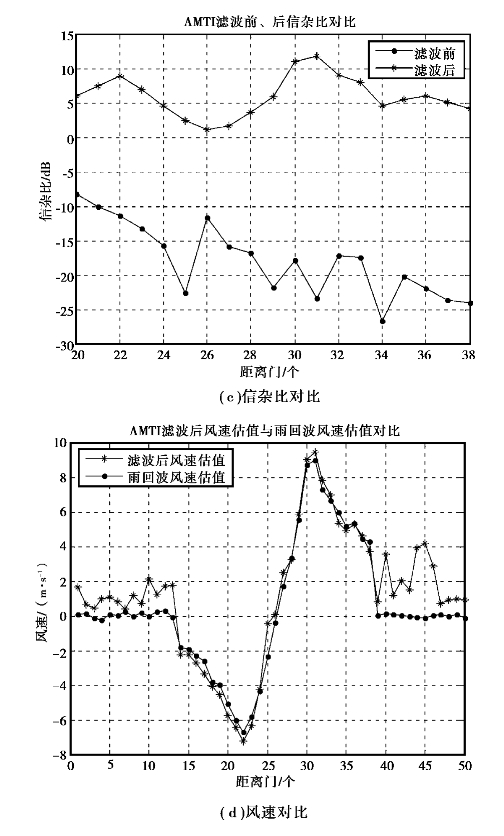
图5.16 AMTI滤波后雷达信号的多普勒谱、信杂比对比及风速对比
图5.16（a）、（b）分别给出了滤波后雷达回波信号的多普勒谱三维图和二维俯视图，由其可清楚地看出在距离门22～30发生了较强的风切变；第25～50个距离门处仍存在较强的零多普勒速度杂波，这是由于在该距离门范围内，滤波前雷达回波信号中的地杂波较强，使得地杂波未滤除干净；而在其他距离门处的杂波几乎被完全滤除；零多普勒速度附近的雨回波和地杂波一起得到了抑制。
由图5.16（c）可知，在地杂波和雨回波均较强的距离门范围（20～38个距离门）内，滤波后雷达回波信号的信杂比与滤波前相比提高13～36dB。
由图5.16（d）可知，经过AMTI滤波后雷达回波信号的风速估值与雨回波风速估值接近。
由上述分析可知，AMTI系统结构简单，运算不复杂，但当运动目标多普勒频率靠近主瓣杂波中心频率时，AMTI抑制地杂波的同时，也强烈抑制运动目标回波。因此，它不适合用于对低速运动目标检测有特殊要求的场合。