5.4.3 最小二乘格形联合过程估计器
最小二乘格形(Least Square Lattice,LSL)联合过程估计器(简称估计器)是自适应噪声对消器(ANC)的一种实现形式[41-44]。该估计器由基于复形式的平方根归一化最小二乘格形估计算法的自适应预测器和基于最小二乘的组合器组成。最小二乘算法是一种以期望响应和输出信号之间误差的平方和最小为准则的。
图5.22给出了该估计器结构,其中虚线框内为M阶自适应预测器,该预测器采用复平方根归一化最小二乘格形估计算法[48]。本人和参考文献[48]的作者共属一个课题组,共同研究地杂波建模与抑制算法,共同研究一种归一化最小二乘格形联合过程估计方法,其具体算法描述如下:
步骤1:初始化
R0=0,T0=0,eb0,0=0,ef0,0=0,e0,0=0,K=0,H=0
步骤2:对信号进行方差估计,同时计算归一化前向预测误差序列
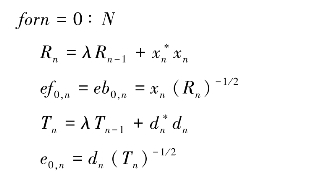
若步骤2中1/x的x出现x=0的情况,则令1/x=1。
步骤3:计算估计器的回归系数、反射系数和归一化后向预测误差序列,其计算过程是一个递归过程,即
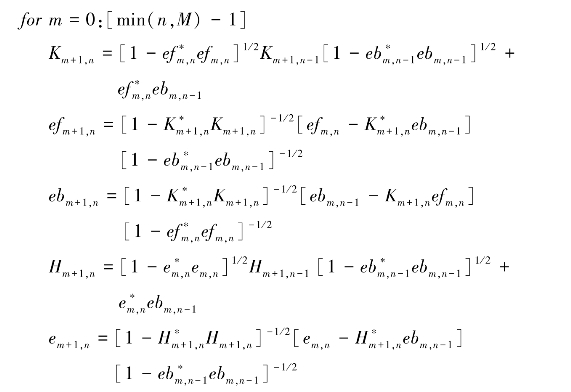
在上述算法中,dn是期望信号;xn为参考信号;eM,n是估计器最后一阶的误差信号,也是其输出信号;Hm+1,n是估计器第m+1阶的n次回归系数;N为数据序列点数;M为格形最大阶数;λ为指数权重因子(0<λ<1);Rn为xn的方差估计;Km+1,n为第m+1阶的n次归一化反射系数;efm+1,n为第m+1阶归一化前向预测误差的n次序列;ebm+1,n为第m+1阶归一化后向预测误差的n次序列。
在上述算法的运算过程中,有两个基于归一化LSL算法的最优估计同时发生:
①将相关输入采样序列xn,xn-1,…,xn-M+1转换为相应的非相关后向预测误差eb0,n,eb1,n,…,ebM-1,n序列。
②把后向预测误差序列eb0,n,eb1,n,…,ebM-1,n作为输入,通过多回归滤波器,以横向滤波器的形式,对期望响应dn进行估计。
上述算法还具有以下特点:与直接实现相比,格形结构具有较低的与有限字长有关的计算误差;与非归一化格式相比,归一化格式对存储容量要求低,且计算复杂度也降低;采用复形式的算法,适用于对复数数据的处理;最小二乘算法具有较快的收敛率;引入了指数加权因子λ,用此因子对输入信号加指数权,时间越近加权越大,这样使算法更能反映当前情况。因此,该算法对雨回波和地杂波回波等非平稳信号具有较强的适应性,可采用该估计器对雨回波和地杂波回波信号进行滤波。
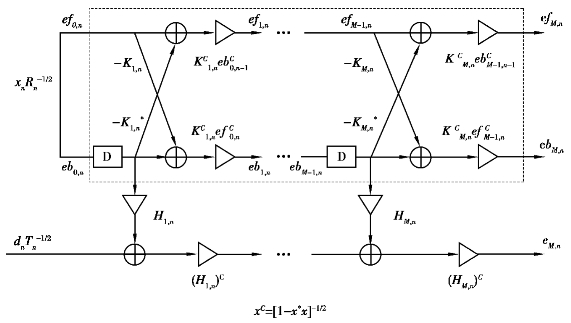
图5.22 估计器结构
上述算法在对雷达回波信号进行滤波的应用中,选取dn为雷达回波信号即总回波,它主要由两个非平稳不相关的信号组成,分别为气象回波信号Wn和地杂波Cn;xn为参考输入信号,一般选取与Cn高度相关的信号,相关程度越高,滤波效果就越好,此处选取地杂波模型产生的信号即地杂波本身Cn作为参考输入信号;估计器的输出信号eM,n即为进行地杂波消除后的输出信号,其期望为气象回波信号Wn。
由于上述算法中,参数M和λ的不同取值可使其滤波效果不同,下面将给出在风切变雷达地杂波抑制的应用中,两种确定M和λ值的情况。
(1)仿真参数选取
由于算法中参数M和λ的不同取值可使滤波效果不同,下面将风速误差和信杂比作为参数选取的标准,讨论不同参数条件下的滤波效果并选取最佳参数值。
1)风速绝对误差作为标准选取参数
此处把第30条扫描线上的风速误差作为标准选取估计器的最优参数M和λ,即把滤波后该扫描线上的风速误差绝对值均值和风速误差绝对值标准差作为标准,其值越小,视为滤波效果越好。此处对风速误差绝对值均值及其标准差的计算参考式(5.29)、式(5.30)。表5.5给出了不同M和λ值的估计器对雷达回波信号滤波后,第30条扫描线上其风速误差绝对值均值及标准差。
表5.5 不同M和λ的估计器滤波后输出信号的风速误差
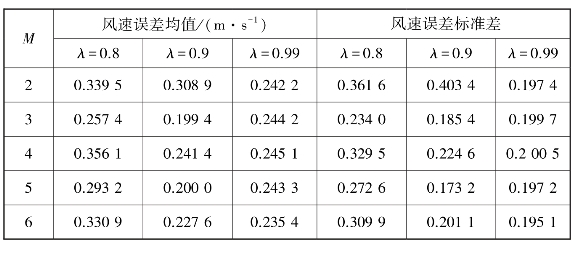
由表5.5可知,当M=3,λ=0.9时,经过估计器滤波后的雷达回波信号的风速误差均值最小,其相应的风速误差标准差也较小。因此,当把风速误差作为标准时,应选取M=3,λ=0.9。
2)信杂比作为标准选取参数(https://www.daowen.com)
此处把第30条扫描线上的信杂比作为标准选取参数M和λ,即把滤波后该扫描线上的信杂比均值和标准差作为标准,信杂比均值越大、标准差越小,视为滤波效果越好。此处对信杂比均值及其标准差的计算参考式(5.32)、式(5.32)。表5.6给出了不同M和λ值的估计器对雷达回波信号滤波后第30条扫描线上的回波信号的信杂比均值及标准差。
表5.6 不同M和λ的估计器滤波后输出信号的信杂比
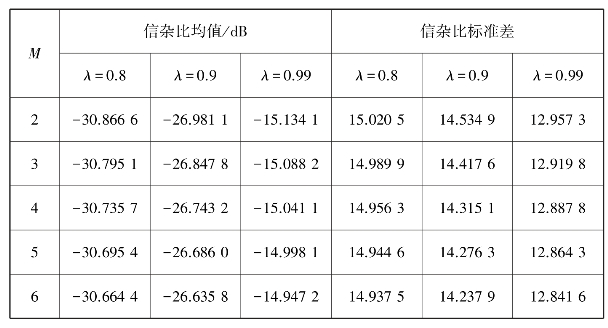
由表5.6可知,对于相同的阶数M,λ越大信杂比均值明显增大,而信杂比标准差越小,因此选取λ=0.99;当λ=0.99时,M越大,则信杂比均值越大、标准差越小,但其各阶之间差值较小,考虑到滤波器阶数M越大,算法执行时间越长,故不宜使M过大,此处选取M=3。因此,选取
M=3,λ=0.99。
3)两种参数选择标准对比
把整个扇面所有扫描线上的风速误差和信杂比作为标准,将上面确定的不同M和λ组合的滤波效果进行对比。
①风速误差绝对值均值对比
根据式(5.29)对第j(1≤j≤NLINE,NLINE=60)条扫描线上的风速误差的绝对值均值的定义,得到一个扇面所有扫描线上的风速误差绝对值均值对比如图5.23所示。图5.25,中“LSL误差(3,0.99)”和“LSL误差(3,0.9)”分别表示M=3,λ=0.99和M=3,λ=0.9的LSL-ANC对雷达回波进行滤波后得到的风速误差绝对值均值。
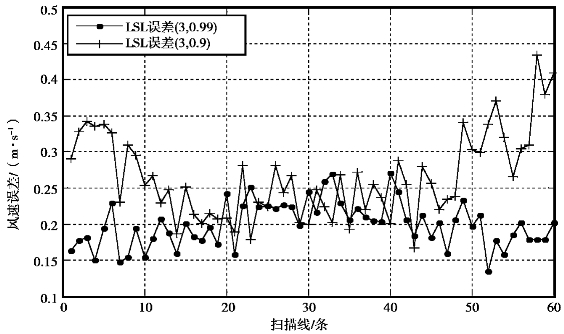
图5.23 不同参数的LSL-ANC滤波后整个扇面上雷达信号的风速误差对比
由图5.23可知,雷达回波信号经过LSL-ANC(M=3,λ=0.99)滤波后,整个扇面上,除中间位置的个别扫描线上之外,其余位置的扫描线上的风速误差均小于经过LSL-ANC(M=3,λ=0.9)滤波后的风速误差。
②信杂比对比
根据式(5.32)对第j(1≤j≤NLINE,NLINE=60)条扫描线上的信杂比均值的定义,得到一个扇面所有扫描线上的信杂比均值对比如图5.24所示。图5.24中,“SCR-LSL(3,0.99)”和“SCR-LSL(3,0.9)”分别表示M=3,λ=0.99和M=3,λ=0.9的LSL-ANC对雷达回波进行滤波后得到的信杂比均值。
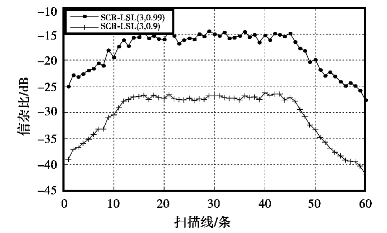
图5.24 不同参数的LSL-ANC滤波后整个扇面上雷达信号的信杂比对比
从图5.24可以明显看出,雷达回波信号经过M=3,λ=0.99的LSLANC滤波后,得到的信杂比均值远大于经过M=3,λ=0.9的LSL-ANC滤波后得到的信杂比均值。
综上分析,当选取LSL-ANC中M=3,λ=0.99时,整个扇面上的雷达回波信号经过滤波后其风速误差较小且信杂比较大,因此,选取M=3,λ=0.99。
(2)滤波效果仿真分析
选取M=3,λ=0.99的LSL-ANC对第30条扫描线上的雷达回波信号进行滤波,滤波后其多普勒谱三维谱和二维俯视图分别如图5.25(a)、(b)所示;图5.25(c)给出了地杂波和雨回波均较强的距离门范围(20~38个距离门)内的滤波前后的信杂比对比;滤波后雷达回波信号的风速估值与雨回波风速估值的对比如图5.25(d)所示。
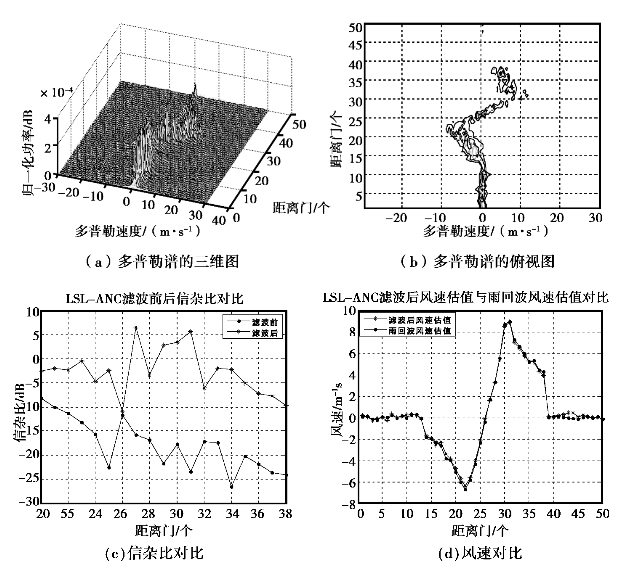
图5.25 LSL-ANC滤波后雷达信号的多普勒谱、信杂比对比及风速对比
图5.25(a)、(b)分别给出了滤波后雷达回波信号的多普勒谱三维谱和二维俯视图,由此可以清楚看出在距离门22~30发生了较强的风切变,在1~13个距离门处,存在零多普勒速度处的较强地杂波,但由于该距离门范围内的雨回波风速在零附近,因此,风速估值几乎不受地杂波的影响。
由图5.25(c)可知,在地杂波和雨回波均较强的距离门范围(20~38个距离门)内,滤波后雷达回波信号的信杂比与滤波前相比提高了2~30dB。
图5.25(d)给出了滤波后的风速估值与雨回波风速估值对比,由该图可知,滤波后雷达信号的风速估值接近雨回波风速估值。
由以上分析可知,风切变雷达回波信号经M=3,λ=0.99的LSL-ANC滤波后,可基本实现地杂波对消。
