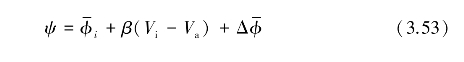3.4.2 目标回波信号建模
由于机载雷达与气象散射体单元之间有相对运动,因此,多普勒频移包括两个部分:飞机的速度和气象散射单元速度。设载机在目标视线方向上的速度为V,单元平均径向速度为Vr(指向雷达为正),载机与散射单元起始距离为r,载机离风切变气象散射单元的距离r(t)则随时间的变化表示为
![]()
相位γ=-4πr(t)/λ+ψ的时间变化率为
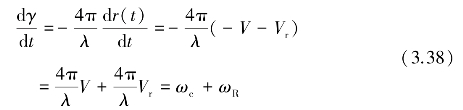
式(3.38)即为多普勒频移表达式,它包括两部分:一部分是由载机引起的多普勒频移ωc;另一部分则是由风切变气象目标运动引起的多普勒频移ωR。式(3.38)表明;可从回波信号中提取由风切变雨回波目标运动引起的多普勒频移ωR信息,以提取目标的径向速度。
设雷达的发射功率为Pt,天线增益为G,目标斜距为R,雷达工作波长为λ,目标的散射率为ρ,L为系统损耗,η是目标的体反射率,Vc是雨目标体积单元,r为雷达到目标的距离。则由基本雷达方程[22]可推得风切变目标雨回波的平均功率为

设目标的有效散射面积为σ′,则风切变目标雨回波的平均功率[23]为

其中,Vc为波束照射的体积,目标的体反射率为[54]
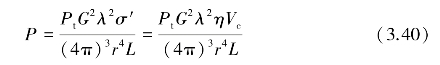
式中,D是圆球之直径,|K|2为散射粒子的介电常数,对于冰与水常取0.20,0.93。![]() ,称为反射率因子。
,称为反射率因子。
因此,给定反射率因子,计算出η,从而求得目标雨回波平均功率。假设雷达发射信号为常用的窄带信号,可近似写为
![]()
其中,当u的变量在0到脉冲宽度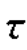 之间时,u(t)取1;否则取0,f为载频。那么,回波信号可看作发射信号的延迟形式,其振幅则乘上一个比例因子K,设γ为复反射系数,令
之间时,u(t)取1;否则取0,f为载频。那么,回波信号可看作发射信号的延迟形式,其振幅则乘上一个比例因子K,设γ为复反射系数,令
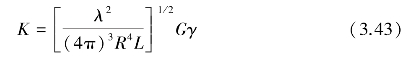
则回波信号的数学表达式可写为
![]()
其中,时延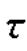 为时间的函数,即
为时间的函数,即
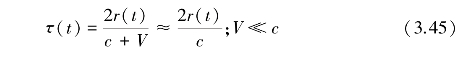 (https://www.daowen.com)
(https://www.daowen.com)
将式(3.37)代入式(3.45)得到
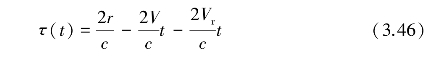
将式(3.46)代入式(3.44)得到
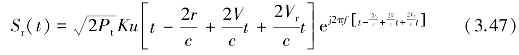
其中,2r/c=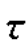 为目标回波的延迟;(2V/c+2Vr/c)f为目标回波的多普勒频移,包括由载机运动引起的多普勒频移和由风切变气象目标运动引起的多普勒频移。
为目标回波的延迟;(2V/c+2Vr/c)f为目标回波的多普勒频移,包括由载机运动引起的多普勒频移和由风切变气象目标运动引起的多普勒频移。
因此,对于风切变气象目标散射体,雷达的目标回波信号可表示为[34]
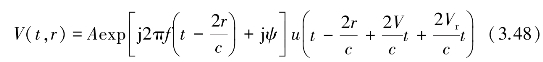
其中,2r为入射波和散射波传播的总路径长度;ψ为由散射体引入随机相位;f为载频;A为回波信号幅度,A=![]() ,P为风切变目标雨回波的平均功率。
,P为风切变目标雨回波的平均功率。
风切变信号回波由两部分组成:气象回波和地杂波。故建信号模型必须建两个模型。信号模型中数据的处理是在零中频之后,如图3.15所示。

图3.15 目标回波信号处理阶段
具体来说,不管是地杂波,还是风切变信号雨回波,对每个距离门内的回波,都可由式(3.49)、式(3.50)来计算。令Vi,Va分别为风切变散射微元和飞机沿径向的速度分量,β=2π/λ为常数,Δω=ωi+ωa=β(Vi-Va)=2π(Vi-Va)/λ,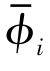 为散射体随机相位,
为散射体随机相位,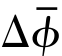 为发射相位误差,
为发射相位误差,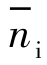 (nTs),
(nTs),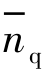 (nTs)为相互独立的接收机噪声。n代表第n个脉冲,Ts代表脉冲时间间隔,则目标回波信号的同相分量I和正交分量Q分别表示为[24,131-133]
(nTs)为相互独立的接收机噪声。n代表第n个脉冲,Ts代表脉冲时间间隔,则目标回波信号的同相分量I和正交分量Q分别表示为[24,131-133]
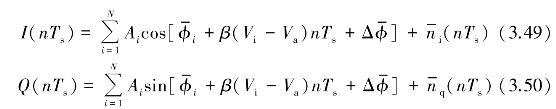
在脉冲多普勒雷达中,存在距离和速度模糊问题,所以最大的不模糊多普勒速度设为Vmax=PRF(c/4fs)=30.032 258m/s,建立的风场的最大速度小于20m/s,不超过最大的不模糊速度,因此可以直接建立风场模型,通过频域来分析回波信号的特征因子。
风切变的雨回波信号的主要特征是风场的风速度变化,散射微粒对发射信号的散射产生的回波信号,这个仿真主要是雨回波信号的相位和幅度变化,即由多普勒频移和风场反射率、反射单元的单位雷达截面积、天线增益决定。
信号幅度Ai由雷达方程和反射率因子确定,即
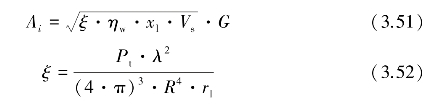
其中,ξ为雷达方程常数,λ为波长,rl为接收机信号损失,xl为衰减因子,ηw为风切变风场反射率,Vs为散射微元的体积,G为天线增益,R为散射单元到天线的距离。
信号相位主要由多普勒频移决定,多普勒频移由两部分组成,分别是Vi和Va,所产生的ωi和ωa,总的雨回波信号相位为