三、地下水的运动
地下水以不同形式（强结合水、弱结合水、毛细水和重力水等）存在于地层的空隙中。除了强结合水外，其他几种水在包气带和饱水带中都参与了运动。弱结合水虽在重力下不能运动，但在一定水头差的作用下，不但能运动，而且还能传递静水压力。粉质黏土、黏土层在一定水头差的作用下也透水。以往的研究多集中于饱水带重力水的运动，但实际生产中提出的不少问题涉及包气带水以至结合水的运动规律。
（一）基本概念
1.水头
考虑地下水位以下土层中的单元体A（图4-7），地下水位以下所有孔隙都是连通的，而且充满水，因此单元体A中的水具有静水压力u w。如果在单元体A处插入一根开口管子（通常称测压管），水将在管中上升，一直到管底端的水压力与u w平衡为止，亦即
式中 γw——水的重度，k N/m3；
h w——A至测压管水面的铅直距离，通常称压力水头，m；
u w——静水压力，又叫孔隙水压力，k N/m2。
这里必须注意区别三个水头：压力水头h w、位置水头Z和总水头H。位置水头Z指的是所考虑的单元体至某一任意指定基准面的铅直距离；总水头H指的是压力水头与位置水头之和，亦即
一般来说，水总是从水头高处流向水头低处，这里的水头是指总水头H，而不是指压力水头h w或位置水头Z。在图4-7中，h w A＞h w B，Z B＞Z A，但因H A=H B，故水并不流动。考虑孔隙水压力u w的绝对值时，需要注意的是压力水头h w；在地下水位处，h w=0，所以u w=0，u w沿土层深度呈线性变化。考虑水的流动问题时，需要注意的是总水头H，又称测压管水头（测压管中的水面至某指定基准面的铅直距离）。
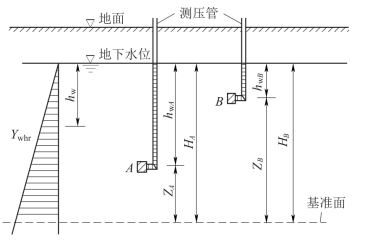
图4-7 地下水位以下土层
2.动水压力
水在土的孔隙内流动时受到土粒（骨架）的阻力，从作用力与反作用力大小相等、方向相反的原理可知，水流过时必定在土的颗粒骨架上产生压力。单位体积土颗粒骨架所受到的压力的总和，称作动水压力G D（k N/m3）。
渗流由下而上，动水压力大于土的有效重度，会产生渗流破坏。渗流破坏可能造成严重的工程事故，必须加以重视。此外，还要留意潜蚀或管涌的现象。它们也属于渗流破坏，整个土体虽然稳定，但细颗粒被水从粗颗粒之间带走，如任其发展，则孔隙扩大，水的实际流速增大，稍粗颗粒亦被带走，便会形成孔道，恶性循环，孔道不断扩大、加深，最终造成严重破坏。管涌现象是由于水力坡度太大所致，特别是不均匀系数μu＞10的无黏性土在较小的水力坡度（0.3～0.5）下就可能出现管涌。因此，作为防止渗流破坏（无论是流土、流沙还是管涌）的根本措施，设计中应尽可能减小水力坡度，必要时在水流逸出处增设反滤层（由细到粗的过渡层）。
3.渗透与渗流
地下水在岩土空隙中的运动称为渗透。由于岩土空隙的大小、形状和连通情况极不相同，从而形成大小不等、形状复杂、弯曲多变的通道（图4-8）。在不同空隙或同一空隙中的不同部位，地下水的流动方向和流动速度均不相同，空隙中央部分流速最大，而水流与颗粒接触面上的流速最小。渗透是岩土中实际存在的水流，其特点是在整个含水层过水断面上是不连续的。如果按其实际情况来研究它，在理论上和实际上都将遇到巨大困难，对于实际应用也毫无意义。因此，通常根据生产实际需要对地下水流加以简化，即用假想的水流模型去代替真实的水流。一是不考虑渗流途径的迂回曲折，只考虑地下水的流向；二是不考虑岩土层的颗粒骨架，假想岩土的空间全被水流充满（图4-9），这种假想水流称为渗流。
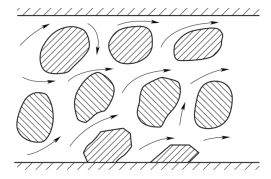
图4-8 渗透示意图
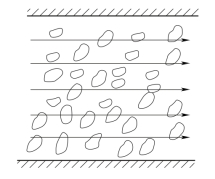
图4-9 渗流示意图
4.层流与紊流
地下水在饱水岩层中并非静止不动的，它是从含水层中水位较高的地方向水位低的地方运动。根据实际观察和试验证实，水流运动有两种基本状态，即层流和紊流。
水质点运动连续不断、流束平行而不混杂为层流状态，如图4-10所示；水质点运动不连续，流束混杂而不平行的为紊流状态，如图4-11所示。
研究表明，水流的运动速度不大时，呈层流状态；当水流速度超过某一临界数值时，就由层流状态转为紊流状态。地下水在岩石的孔隙、裂隙中运动时水流速度较慢，所以，绝大多数情况下地下水运动呈层流状态，只有在很大的裂隙和岩溶洞穴中运动的地下水才呈紊流状态。
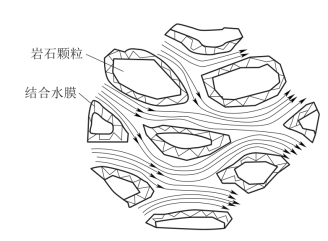
图4-10 层流示意图
图4-11 紊流示意图
5.稳定流和非稳定流
运动规律一般可以通过其运动要素（动水压力、流速、加速度等）在时间和空间里的变化来描述。如果某一水流的运动要素仅仅是空间坐标的函数，而与时间无关，这种水流称为稳定流。如图4-12（a）所示，当水箱内水位保持不变，水从箱壁孔口流出，其压力和流速与它在空间的位置有关，而与时间无关，这种水流是稳定流。
当水流中各点的运动要素不仅与空间坐标有关，且需随时间变化而不同，这种水流是非稳定流。如图4-12（b）中的水箱中的水量没有补给，随着时间的增长，水量减少，水头降低，各点压力减小，其他运动要素也随时间而改变。
（二）线性渗流定律
1.达西定律
地下水的运动有层流、紊流和混合流三种形式。层流是地下水在岩土的孔隙或微裂隙介质中渗透，产生连续水流；紊流是地下水在岩土的裂隙或洞穴中流动，具有涡流性质，流线有互相交错现象；混合流是层流和紊流同时出现的流动形式。
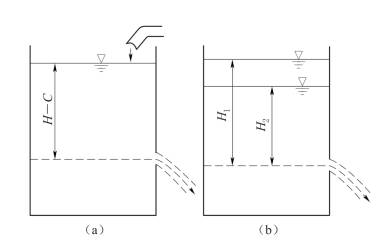
图4-12 稳定流与非稳定流示意图
（a）稳定流；（b）非稳定流
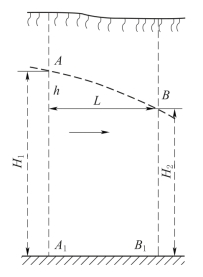
图4-13 地下水层流断面图
AB—潜水面；A 1 B 1—隔水层
地下水在土中的运动（渗透）属于层流（图4-13），且遵循达西（Darcy）线性渗透定律，其公式如下：
其中 h=H 1-H 2
式中 Q——单位时间内的渗透水量，m3/d；
K——渗透系数，m/d；
A——水渗流的断面积，m2；
L——断面间的距离，m；
h——距离为L的断面间的水位差，m；
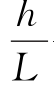——水力坡度，用符号I表示，代表单位长度渗流途径上所产生的水头损失，亦称水力梯度（无因次）；
H 1、H 2——断面AA 1、BB 1上的水位值。
式（4-3）两边同时除以断面面积A后，即得渗流速度v，渗流速度与水力坡度成正比：
当I=1时，得K=v，即当水力坡度等于1时，渗透系数等于渗流速度，它的单位为cm/s或m/d。
由式（4-6）可知，上述的渗透系数K也就是水力坡度等于1时的渗流速度。水在土中的渗流速度v取决于两方面的因素：一是土的透水性（反映为K的大小）；二是水力条件（反映为I的大小），这就是水在土中渗流的基本规律，亦即达西定律。
这里要注意两个问题：①v并不是水在孔隙中真正流动的速度，因为孔隙是弯弯曲曲的。实际渗流途径并不等于L；横截面积A中不全是孔隙，实际过水面积不等于A。因此，实际平均流速大于渗流速度v。但工程实践中关心的不是水质点的真正流速，而是流经整个土体的平均流量。所以用表观的流速v、A、L考虑是可以的，而且更为方便。②达西定律v=KI只适用于砂及其他较细颗粒中。因为孔隙太大时（如卵石、溶洞）流速太大，会有紊流现象，水质点的流线互相交错，不是层流，不再与I的一次方成正比。渗流速度不是孔隙中的实际流速u，它只是换算速度，因为在这个公式中用的断面积并不是孔隙的横断面积。
在一般情况下，砂土、黏土的渗透速度很小，其渗流可以看作是层流，渗流运动规律符合达西定律，渗透速度与水力梯度的关系，如试验所得图4-14中的曲线Ⅰ所示。但是，在某些黏性土中这个公式就不正确。因为在黏性土中颗粒表面有不可忽视的结合水膜，阻塞或部分阻塞了孔隙间的通道。试验表明，I值比较小时克服不了结合水膜的阻力，水渗流不过去，只有当水力坡度I大于某一值I b时，黏土才具有透水性（图4-14中的曲线Ⅱ）。
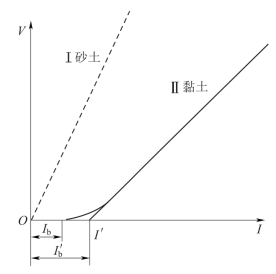
图4-14 渗流速度与水力坡度
如果将曲线Ⅱ在横坐标上的截距用I′b表示（称为起始水力坡度），当I＞I′b，时，达西公式可改写为
2.水力坡度
水力坡度为沿渗透途径水头损失与相应渗透长度的比值。水质点与颗粒在空隙中运动时，为了克服水质点之间的摩擦阻力，必须消耗机械能，从而出现水头损失。所以，水力坡度可以理解为水流通过单位长度渗透途径为克服摩擦阻力所耗失的机械能。
3.渗透系数
渗透系数K反映土的透水性大小，其常用单位为m/s或m/d，一般通过做室内渗透试验或现场抽水或压水试验进行测定。
（1）渗透系数的测定。渗透系数测定的试验装置如图4-15和图4-16所示，有定水头和变水头两种。室内渗透试验的原理如图4-17所示，量测Q后反算K。
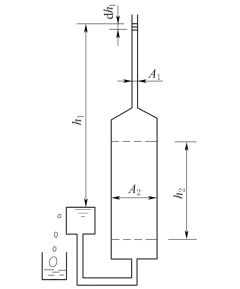
图4-15 定水头渗透系数测定试验装置
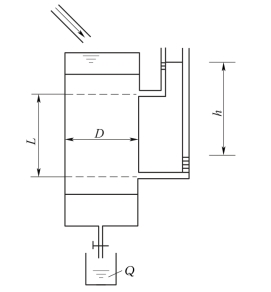
图4-16 变水头渗透系数测定试验装置
（2）渗透系数经验值。表4-4可用于粗略估算土的渗透系数。
表4-4 各类土的渗透系数
（三）非线性渗流定律
地下水在较大的空隙中运动且其流速较大时，则呈紊流运动，此时的渗流服从哲才定律。前面已经谈到，从层流向紊流的转变是逐渐过渡的，没有明显的界线。因此斯姆列盖尔认为，介于层流与紊流之间的流态是一种层流和紊流并存的混合流。
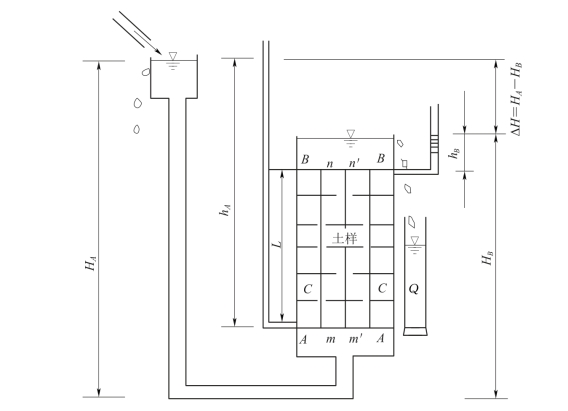
图4-17 一维渗流试验装置示意图
（四）流网
土体中的稳定渗流（水流运动要素不随时间变化，土的孔隙比和饱和度不变，流入单元体的水量等于流出单元体的水量以保持平衡）可用流网表示。流网由一组流线和一组等势线组成。
如图4-17所示，如果在AA面上若干点放置一些颜料，就会出现若干条反映水流方向的流线，如图中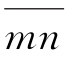
；和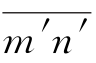
；两条流线之间的空间称为流槽。在AA面上各点的水头均等于H A，故称线AA为等势线，BB和CC也都是等势线，即凡总水头相等的各点的连线称等势线。图4-17所示的方格网（不一定必须是方格）就称流网。
绘制流网的目的是可直观地考察水在土体中的渗流途径，更重要的是可用于计算渗流量以及确定土体中各点的水头和水力坡度。如图4-17所示的一维流动情况，实际上没有必要绘制流网，直接应用达西定律就可计算流量、确定各点的水头和水头差。但实际工程中遇到的很多是二维流或三维流情况，这时绘制流网就很有用。