4.3.1 逐步判别分析
逐步判别分析不同于其他判别分析将全部变量进行分析,同时因为光谱数据量大,将全部变量进行计算会非常困难。在判别分析的过程中,逐步判别法首先是确定有效变量(ZHOU S, et al., 2006; BAEVSKY R W, et al.,2011),综合考察判别式的判别能力之后,将判别能力差的变量自动剔除判别式,当有新变量引入之后,判别式的判别能力不再提高,或者剩下的所有变量依次或者组合引进判别式后,没有引起判别式的判别能力提高,则这些变量为非显著变量,引起判别式判别能力提高的变量为显著变量,显著变量需要保留,而非显著变量需要剔除,至此逐步判别过程结束(PETALAS C, et al.,2006;张菊连等,2010)。
4.3.1.1 逐步判别法的基本思想
在判别问题中,当判别变量的数量过大时,如果不分青红皂白地创建判别函数,不仅计算量大,而且因为变量是中间相关的它很可能减少逆矩阵的计算误差并产生不稳定的判别函数。因此,正确筛选变量的问题成为一个重要问题。有筛查的地方变强度的判别统计分析方法称为逐步判别法。
逐步判别法与一般判别分析法一样,具有许多不同的基本原理,进而产生各种方法。这里讨论的逐步判别统计分析,该方法应建立在多个判别数据的基础上,判别规则为贝叶斯算法的判别函数,其理论基础类似于逐步回归分析,被选中“进和出”的优化算法是基于变量是否是关键,然后逐步引入变量,将每个“最关键”变量同时引入判别公式中,有必要了解前面介绍的变量是否是因为在它们之后引入新变量使其不那么必要和不那么明显(例如,它的作用后来被变量的搭配所取代),有必要及时将其从判别式中删除,直到判别式中没有必须删除的无动于衷的变量,其余变量没有极其重要的变化。当筛选逐渐完成时,可以将数量引入判别公式中。也就是说,每一步引入或划分变量,进行相应的统计检验,这样最终的贝叶斯算法判别函数就只保存了“关键”变量。
4.3.1.2 判别变量附加信息的检验
根据逐步判别解析的基本概念,判别分析应解决两个关键问题:① 一是引入或去除判别变量的重要依据和检验问题;② 判别函数的直接推导问题。这样做的基本原理取决于应该如何判断变量,以测试区分每个总体的额外信息。因此,这里是有关如何识别变量以及它们是否可以提供额外信息来区分每个总体的基本知识。
设有m个总体,G1,G2,…,Gm,相对应抽出来样品数量为n1,n2,…,nm。(n1+n2+…+nm)=n 。每一个样品观测p个指标,得观测数据如下,
第1个总体的样本数据为:
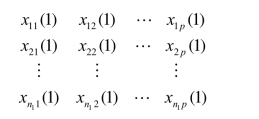
第2个总体的样本数据为:
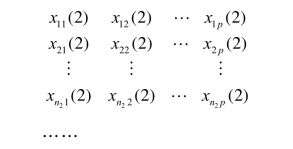
第m个总体的样本数据为:
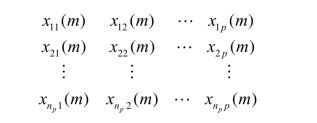
和多个线性回归分析一样,假定每组的样本全是互不相关的正态分布随机向量,每组的协方差矩阵都一样,即
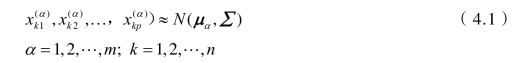
式中 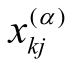 —— α组第k个样品的第j个变量; μα—— α组的均值向量;
—— α组第k个样品的第j个变量; μα—— α组的均值向量;
∑—— 协方差矩阵。
再令全部样品的总均值向量为
![]()
各个总体的样品的均值向量为:

于是,样品的组内离差阵为
![]()
样品的总离差阵为
![]()
为了对这m个总体建立判别函数,需要检验:
![]()
当H0被接受时,表明区分这m个群体是没有意义的,在此基础上,建立的判别函数是无效的。当H0被拒绝时,它表明可以区分m个群体,并且创建的判别函数更有意义。但是,为了区分m个种群的效应,可以对原来选择的p指标进行简化,以达到相同的判别效应,因此,有必要去掉一些没有额外信息的自变量来区分m个群体。
采用维尔克斯统计量(Wilks)Λ:

其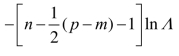 的lim分布是服从于整个样本的χ2[p(m-1)]。
的lim分布是服从于整个样本的χ2[p(m-1)]。
为了进一步考虑这个问题,将p变量分解为两部分,一般通过某种类型的过程已经选择了p-1变量,我们应该检验p变量的提升是否给差分整体带来了附加信息,这意味着要测试p变量的“判别能力”。因此,矩阵W和T被分块:

前p-1个变量的维尔克斯统计量Λp-1为

当增加第p个变量后,p个变量的维尔克斯统计量Λp为
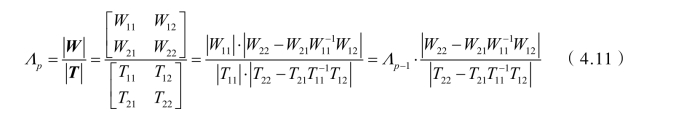 (https://www.daowen.com)
(https://www.daowen.com)
所以有

即
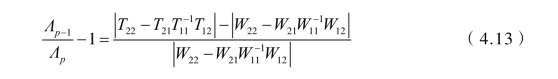
统计量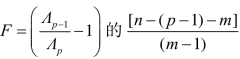 极限分布是F((m-1),(n-(p-1)-m))。F统计量来检验给定前p-1个变量的条件下,增加第p个变量的条件均值是否相等(即是否对区分总体提供附加信息)。
极限分布是F((m-1),(n-(p-1)-m))。F统计量来检验给定前p-1个变量的条件下,增加第p个变量的条件均值是否相等(即是否对区分总体提供附加信息)。
4.3.1.3 引入和剔除变量、检验统计量
① 假设已经测算了l步,并已引入了x1,x2,…,xl ,测试了步骤l+1中添加新变量的“判别能力”,于是将变量分为2组,第一组是已经引入的前l个变量,第二组只有一个变量xr,这些l+1变量的色散矩阵和总离散矩阵仍记录为W和T。

其中,![]()

其中,![]()
维尔克斯统计量

令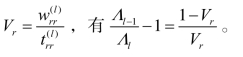
根据附加信息检验准则,其引入变量的依据是Vr,检验统计量为
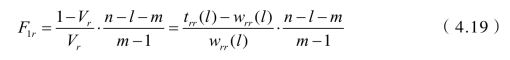
其引入变量的检验统计量服从分布F(m-1,n-l-m)。
② 若剔除变量xr(1≤r≤l )是第l+1步,则第l+1步剔除变量xr等价于第l步引入xr,令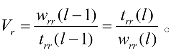
其剔除变量的依据是Vr,检验统计量为
![]()
其剔除变量的检验统计量服从于分布F(m-1,n-(l-1)-m)。
4.3.1.4 矩阵变换
设初始的组内离差矩阵为(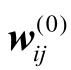 ),初始的总的离差矩阵为(
),初始的总的离差矩阵为(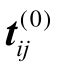 )。假如已经进行了l步,引入了l个变量,那么第l+1步无论是引入还是剔除变量xr,都要进行如下转换:
)。假如已经进行了l步,引入了l个变量,那么第l+1步无论是引入还是剔除变量xr,都要进行如下转换:

4.3.1.5 建立判别式
假设最终引入了l个变量,并得到最终变换矩阵(wr r(l )),则第k组的判别函数为:
![]()
k=1,2,…,m ;i∈已入选变量。

k=1,2,…,m ;i∈已入选变量。
式中xki—— 第k组第i个变量的均值。
将每个样品x=(x1,x2,…,xp )′分别代入k个判别 式 中,若y(h/x)= max1<g≤mx(g/x ),则x属于第h个总体。为了对已经引入的L个变量对于区分m个组的能力进行综合检验,可采用Bartlett给出的χ2分布近似统计量。
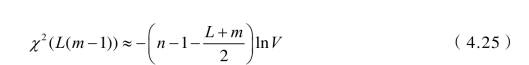
式中V—— Wilks统计量:

式中 r0,r1,…,rl -1—— 逐次引入或剔除的变量序号。
