4.4.1 随机森林
随机森林(Randomforest,RF)(CULTER A, et al.,2012)是一种基于分类树的算法,它通过对大量分类树的汇总提高了模型的预测精度。随机森林快速、灵活,是挖掘高维数据的一种稳健方法,同时也是分类树和回归树的延伸。即使在存在大量特征和少量观测值的情况下,随机森林也表现良好。随机森林的树形构建过程隐含地允许特征之间的互动和特征之间的高度相关,随机森林结构如图4.14所示。
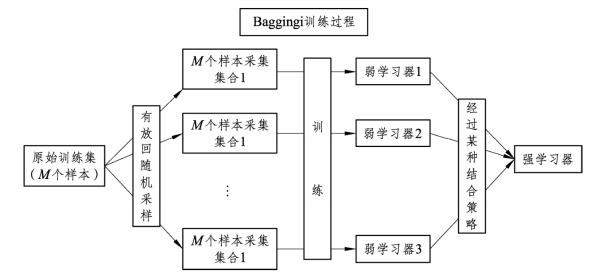
图4.14 随机森林结构示意图
4.4.1.1 每棵树的生成规则
假如训练集尺寸为N,针对每棵树来讲,任意并有放入地从训练集里提取N个训练样本(便是bootstrap sample方法,拔靴法取样)作为该树训练集;从这里出发我们能了解:每棵树的训练集都是不一样的,并且里边包括重复训练样本(王晓青,2016)。
如果出现M个特征,即在每一个连接点瓦解时,从M中随机抽取m个特征层面(m << M),使用这m个特征层面中最好特征(最大化信息增益)来切分连接点。在森林生长期间,m的值保持不变。
一开始所提到的随机森林里的“任意”是指此处的2个偶然性(王晓青,2016)。2个偶然性的引入对随机森林的种类特性尤为重要。因为它们引入,促使随机森林不会陷入多重共线性,并具有很好的抗噪水平(例如,对数值数据敏感度低)(王晓青,2016)。
4.4.1.2 随机森林分类效果(错误率)
随机森林分类效果(错误率)与以下两个因素有关:
(1)森林中任意两棵树的相关性:相关性越大,错误率越大(弱分类器应该good且different)(王晓青,2016)。
(2)森林中每棵树的分类能力:每棵树的分类能力越强,整个森林的错误率越低。(弱分类器应该good且different)(王晓青,2016)。
减小特征选择个数m,树的相关性和分类能力也会相应的降低;增大m,两者也会随之增大,因此重要环节怎么选择最佳的m,也是随机森林的一个主要参数(王晓青,2016)。
4.4.1.3 OOB(袋外错误率)(https://www.daowen.com)
上文提及,搭建随机森林的重要环节便是怎么选择最佳的特征数m这一主要参数,要解决这些问题重要依据测算袋外差错率(Out-of-bag Error,OOB Error)。
随机森林的一个重要优点是无需交叉验证它们或使用单独的测试集来获得偏差的无偏估计。它可以在外部进行评估,换句话说,可以在形成过程中建立偏差的无偏估计。
在搭建每棵树时,对测试集用了不同的Bootstrap sample引导程序示例(任意和插入提取)。因此,对于每棵树(假设第k棵树),大约1/3的练习没有参与第k棵树的形成,它们称之为第k棵树的OOB样本。但是,此采样特征允许每个人执行OOB可能性,其计算方法如下:
(1)对于每个样本,将树的分类状态测量为OOB样本(约占树的1/3);
(2)采用简单多数网络投票作为样本的类型结论;
(3)然后使用假除数与样本总数的比率作为随机森林的OOB误分率。
OOB误分率是随机森林泛化误差的一个无偏估计,它结论无限接近需要很多测算的k折交叉验证。那样,就可以根据较为OOB误分率来选择一个比较好的特征数m。
4.4.1.4 随机森林参数
在scikit-learn中,RF的分类算法是Random Forest Classifier,重归器是Random Forest Regressor。RF的参数也包含两个部分,第一部分是Bagging框架的参数,第二部分是一棵CART决策树的参数。
4.4.1.5 随机森林的特点
随机森林能够处理具有高维特征的输入样本,而且不需要降维;能够评估各个特征在分类问题上的重要性(Feature Importance);在生成过程中,能够获取到内部生成误差的一种无偏估计(OOB);对于缺省值问题也能够获得很好的结果(纪宇楠,2018)。
随机森林是一种有效的分类预测方法,对于噪声和异常值有较好的稳定性,较为适合处理高维光谱数据,对于缺失数据,仍可以维持准确度,对于数据集不均等的情况,随机森林可以平衡误差,与其他机器学习方法相比,随机森林的一个优势是其计算速度。额外的优点包括重要性测量的可用性和方便的特征选择程序。后者还允许将随机森林与其他机器学习方法相结合。具体来说,最重要的特征可以通过在第一步使用随机森林来选择。在特征数量较少的情况下,可以在第二步使用其他更耗费计算机时间的机器学习方法。但是当随机森林中的决策树过多时,训练时间和所需的空间将会增加,同时随机森林模型不易解释。
