4.3.5 Fisher线性判别分析
Fisher线性判别分析(FLD),也称线性判别式分析(Linear Discriminant Analysis,LDA)(周唯,2018),广泛应用于特征提取与降维。FLD力图找到一组最理想的投影方向,在各种投影方向上,能够比较好地区别练习集中化归属于不一样类型的样本。这类可分性,在数学上能够采用不同的规范去衡量。在其中较为常用的一种界定为:在投影后测试集上,类间离散度矩阵的行列式和类内离散度矩阵的行列式的比率更大化,FLD可以在扩大类间离散度的前提下降低样本的类内离散度,从而使在投影空间内,不一样类型的样本尽可能分开,而归属于同一类型的样本将汇聚在一起,因此更适合鉴别。
FLD是一种基于样本类别的整体特征提取的有效方法。在采用PCA方法进行特征提取的前提下,充分考虑了运动样本的类间信息内容。FLD的原理是找到一个理想的投影轴,使各个样本在这个轴上的投影之间的距离尽可能远,每个类中样本的投影尽可能接近,这样分类的实际效果最好,在减小到最小类内间距的同时,类之间的距离最大化。
Fisher方法在解决子空间缩小问题上采用此方法。如果将多维度特征空间一个点投影到一条直线上,就能将特征空间转化成一维,这在数学上是非常容易办得到的。但是,在高维空间里非常容易分开的试品,将它们投影到随意一根直线上,有可能会不一样类型的试品就混在一起没法区别。如图4.9(a)所示,向x1轴或x2轴的投影是无法区分的。如果线绕起点旋转,极有可能找到一个方向,并且样品在这些方向上投影在直线上,并且可以很好地分离各个样品,如图4.9(b)所示。因此,直线方向的选择非常重要。一般来说,总能找到一个好的方向,这样试样就很容易在这些方向上投射到直线上。如何找到这个更好的直线方向,如何实现投影向最佳方向的变换,是费舍尔优化算法需要解决的基本问题,而这个投影变换恰好就是我们寻求的解向量w*。
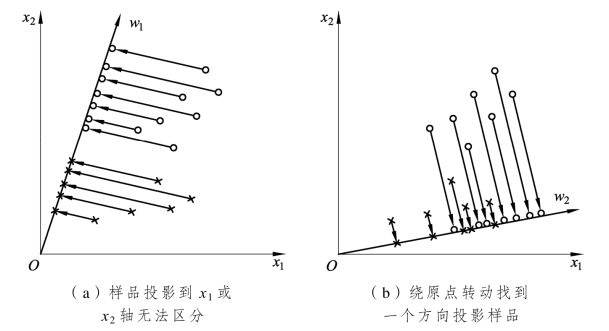
图4.9 两种投影方法的示意图
这里只讨论两分类的问题,训练样本集是 X={x1,…,xn },每一个样本是一个d维向量,其中w1类的样本是X1={x11,…,xn1 1},w2类的样本是X2={x12,…,xn 12}。我们要寻找一个投影方向W(W是一个d维向量),投影以后的样本变成(周唯等,2018)
![]()
在原样本空间中,类均值向量为
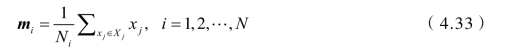
定义各类的类内离散度矩阵(Within-class Scatter Matrix)为
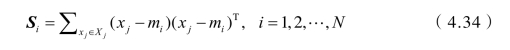
总类内离散度矩阵(Pooled Within-Class Scatter Matrix)为(周唯,2018)
![]()
类间离散度矩阵(Between-class Scatter Matrix)为(周唯,2018)
![]()
Fisher判别准则变为Rayleigh商

最佳投影方向
![]()
决策规则
![]()
4.3.5.1 算法描述
1. 留一法
留一法是K折法的一种非正常情况。在K折法中,把全部训练集S分为k个不相交的子集,假定S里的训练示例数量为N,那样每一个子集有N/k个训练示例,对应的子集称之为 {s 1 ,…,sn }。每一次从分得的子集中里边,拿出一个作为测试集,其他k-1个作为训练集,依据训练训练出实体模型或是假设函数。并把这一实体模型放进测试集上,获得归类率,测算k次求取的归类率的均值,作为该实体模型或是假设函数的实际归类率。
当取K的数值样本数量N时,将要每一个样本作为检测样本,其他N-1个样本作为训练样本。那样获得N个分类算法,N个检测结果。用这样的N个过程的均值去衡量模型特性,这便是留一法。UCI数据信息集中化,因为数据信息数量偏少,选用留一法能使样本使用率最大。
2. Iris数据集
在Iris数据集中,有150个样本,共三类Setosa、Versicolour、Virginica,一共有4维特征,分别为sepal length、sepal width、petal length、petal width.(https://www.daowen.com)
在Fisher线性判别方式中,因为只能判别两大类,所以把Iris数据集分三种情况:1-2类,1-3类,2-3类,各自分辨每一种状况的Fisher判别准确率。用留一法对练习和测试样本开展区划以后,算出每一类中间的最佳投射方位W1、W2、W3以后,然后再进行准确率测试。
3. Sonar数据集
在Sonar数据集中,有208个样本,共两类:字母“R”(岩石)和“M”(矿井),而且有一共有60维的特征。
对于多维度的现象,我们可以得到数据在不同维度中的Fisher线形辨别准确率。在这时候出现了一个难题:怎样在60维中选择维数?假定我们应该测算在42维的准确率,选什么维数才比较接近真实值?对于此问题,本书选用数次抽样求平均的办法,对样板特征开展打乱,选前42维的特征来计算,反复10次打乱的过程,求准确率的均值,这可以避开因为一些特征较为便于区别而造成的精确率高过平均的现象。
4.3.5.2 仿真结果
1. Iris数据集
图4.10为在最佳投影方向W0投影的结果,其中黑色的点为W1类,红色的点为W2类,分类阈值为(0,0)点。
从投影点能够得知,第一类和第二类、第一类和第三类间隔尤其远,利用线形辨别能够很好地把它们分开,而第二类和第三类间隔较近,但利用线形辨别也可以基本上将其分开,得出来的准确度也能够证明这一点。
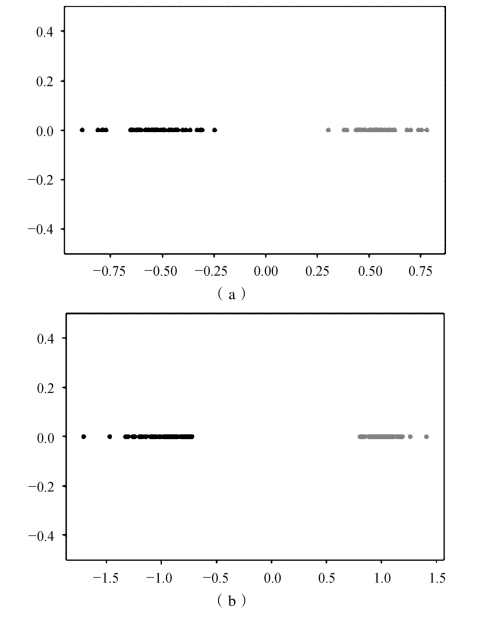
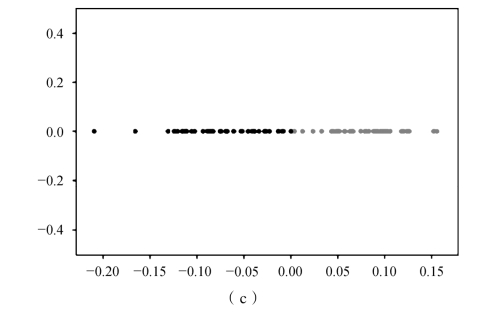
图4.10 Iris数据集仿真投影结果
2. Sonar数据集
首先对60维的时候进行投影,得到两类的投影结果,如图4.11所示。
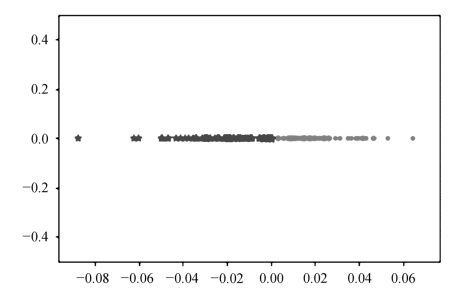
图4.11 Sonar数据集60维投影结果
从图4.11可以看出,两类的分界面处交集较多,准确率约为0.75。
将60维扩大到1~60维,得出每一维的准确率,针对不同维数,画出曲线图(图4.12、图4.13)。
图4.12 Sonar数据集不同维数的准确率
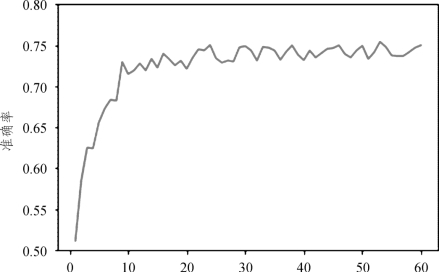
图4.13 利用Fisher线性判别的准确率
从图4.13可以看出,在只有一维的时候,利用Fisher线性判别得出的准确率约为0.5,随着维数的增长,准确率慢慢提高,最终趋于一个稳定值0.75左右。
4.3.5.3 代 码
GitHub地址如下:
Pattern recognition / LDA
https://github.com/Fangzhenxuan/AI_Projects.git
