4.3.3　连续小波变换

小波变换在傅里叶变换的前提下给出了变动的时间窗定义使用时间- 尺度域依据高频低频信息的需求来调节时间窗长短尺度与次数反比关联从根本上解决了非平稳随机过程高、低频率时长局部化难题。基本上小波是小波变换中一个很重要的组成要素它是一种具有独特损耗属性的实值函数。较为有名的小波有：Daubechies、Coiflets、Symlets、Morlet、Meyer等（田捷等，2004；陈武凡，2002）。

连续小波变换具备线形性、平移不变性、伸缩式共转性、自相似性和冗余设计等关键特性。因为连续小波变换存有多余，在具体应用中为了能重新构建数据信号，必须对小波变换的尺度因素和偏移因素开展离散化，进而产生离散变量小波变换。

连续小波变换。采用连续小波变换，经过多次实验，发现墨西哥帽（Mexh）小波基函数适用于提取不同类别青花瓷碎片的光谱隐含信息，所以采用墨西哥帽小波基函数对原始光谱进行10层小波变换，生成一系列小波系数（VOHLAND M，et al., 2016；WANG G Q, et al., 2016；于雷等，2016）。

式中　a—— 伸缩因子；

b—— 平移因子；

λ—— 青花瓷高光谱数据的波段数。

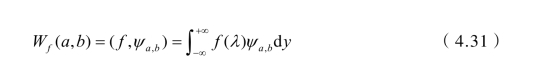
式中　fλ—— 青花料的光谱反射率；

小波系数Wf(a,b)包括二维，分别为波长（350～950 nm）与分解尺度（1, 2, 3,…, 10），所以Wf(a,b)的行是分解尺度数，列为青花料波长数的矩阵。