实施过程(根据学生的汇报录音整理)
我们小组研究的重点是倒立摆。
什么是倒立摆?先从一个生活实例开始。相信大家都有过,努力保持它不倒的经历(图4—9),我们怎么做到了呢?因为大脑调节的结果,大脑通过棍子的受力而使我们移动。那么我们来讲一下,机器可以代替人脑控制吗?当然是可以的。倒立摆就是一种支点在下、重心在上,横空稳定的一个系统或者装置。

图4—9 相信每个人都有使手中的棍子保持不倒的尝试
我们为什么要选它为研究对象?因为倒立摆具有高阶次、不稳定、多变量、强耦合等优点。这种性能有广泛的应用前景,比如半导体及精密仪器加工、机器人控制技术、人工智能、导弹拦截控制系统、航空对接控制技术、火箭发射中的垂直度控制(火箭在空中的姿态调整就可以利用倒立摆控制方法实现)、卫星飞行中的姿态控制和一般工业应用等。倒立摆也是很好的基础实验平台,具有很重要的作用(图4—10)。
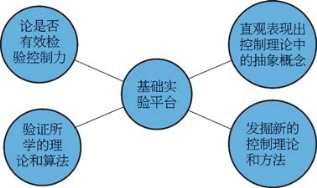
图4—10 倒立摆作为基础实验平台的作用
通过对倒立摆的研究,深入了解控制理论并设计控制系统。与倒立摆相关的最基本的问题是控制。控制的定义很复杂,但是实际上它就是一个调整到特定的值或者要求的东西。那么我们为什么要研究控制呢?控制无处不在,我们身体自身就是多种复杂控制的结合体。比如说我们自身的温度,我们人体自身就是一个很精准的温度控制系统。不论是在清晨或是在中午,也不论是在寒冬或是在酷夏,人体的温度在正常情况下,一般总是保持在36.8℃左右,偏差不超过0.2℃。也就是说,在正常情况下,人体内的温度控制系统总会根据外界与内部的条件变化,控制人体自身发出的热量和散热量,从而使体温保持为常值。
控制也改变着我们的生活,控制使我们的生活变得越来越好,也越来越简单。比如说相机,早期的手动相机(120相机)拍照,要手动对焦和设置光圈大小等,而现在的数码相机、手机相机:方便易拍、效果完全满足大众需要。实际上它就是智能控制技术(尤其是模糊控制技术)应用的结果。控制改变了相机,也方便了我们的生活。
人在控制里将无所不能,因为一切将尽在掌控之中。许多带“自动”功能的设备、仪器等,都是控制技术的应用。你会“控制”,你将无所不能!
选定了方向,在开始研究之前我们首先要确立一些研究思路(图4—11),这是做任何研究之前都要先去思考好的。
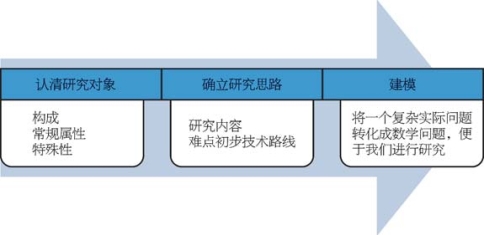
图4—11 研究思路
首先就是我们应该去认清我们的研究对象,就是我们研究的是什么、它的构成是什么,然后它有什么常规属性和特殊性,在明确我们要研究的内容之后,接下来再确定我们的研究思路。就是我们要怎么去研究、有什么难点、用什么方法。
当确立完这个研究思路之后,我们就可以进行这个研究工作—建模。其实这个建模在许多科学研究当中都是非常重要的,建模的过程就是相当于将一个复杂的实际问题转化成一个数学问题,来便于我们进行研究的一个过程。
首先,我们要提出一个实际问题。
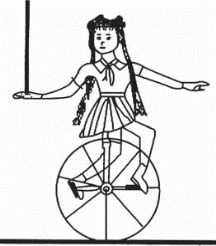
图4—12是一个杂技演员骑着独轮自行车,如何使她手里的摆杆不倒?她通过骑着自行车来这样来回移动,以便找准重心让它保持不倒。
即使是再显而易见的生活现象也可以用理论和公式来解释。杂技演员控制摆杆是通过大脑一系列复杂的调控完成的,那么机器有没有可能实现(替代大脑控制)这个功能呢?
当然,我们不可能一步登天直接分析实物,需要先建立一个仿真模型(图4—13),通过研究这个实物模型,再结合理论分析来得出结论。不过,单就这个简单的问题而言,我们还是可以做一个简易的电脑控制模拟的,其实对我们而言真是个挑战。
我们把杂技演员的独轮车换作导轨,可以左右移动保持摆杆平衡,把各种人体的感知换成摆角传感器和位移传感器。这样就可以用各种数学物理的方法进行研究了。
 (https://www.daowen.com)
(https://www.daowen.com)
图4—12 杂技演员骑着独轮自行车
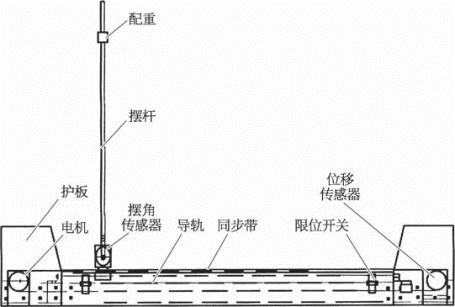
图4—13 建立仿真模型
接下来,我们需要建立物理模型。把实际问题变成一个物理问题。
如图4—14所示的物理模型,显然,为单一刚性铰链、两个自由度动力学问题。因此,依据经典力学的牛顿定律即可满足要求。
接下来就可以分析运动状态,然后进行受力分析了,于是物理问题就变成了纯粹的数学问题。其实建立一个物理模型就是说先把一个实际问题来转化成一个数理问题。我们来设定一些参数,这是根据我们已经学过的一些牛顿定律就可以来得出的。接下来就是我们来对它进行一个受力分析,这样的话就能得到许多表达式。然后把它带进这个动力学的微分方程,最后我们能得到一个系统分析模型,我们可以通过这个模型来描述我们刚才的那个实际问题。
如图所示,设小车的质量为m0,倒立摆的质量为m,摆长为2l。摆的偏角为θ,小车的位移为x,作用在小车上的水平方向的力为F,O1为摆杆的质心。
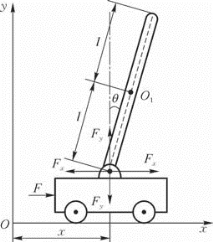
图4—14 建立物理模型
最后,我们可以得到一个系统的精确模型:
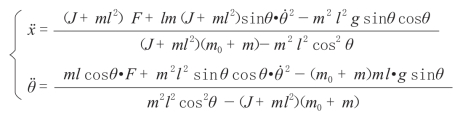
别担心,我并不是要讲我们怎么来运算这个复杂的式子。我们是来介绍我们的研究过程以及研究方法的,而不是来讲课。
有人说过,“倒立摆为什么如此吸引科学家?因为它对自己的理论,永远是个挑战,这样就能逼着你不停地修正、完善”。
通过一系列的修正,简化,以及带入一些实际值(这其中涵盖了多少令人痛苦的过程),最后我们得到了如下模型:
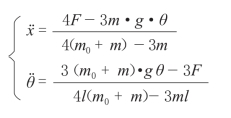
比起初步模型,有很大的改进。
简化完后,我们还需要用Matlab的Simulink图形仿真环境下进行模型验证实验(图4—15、图4—16),来验证我们的模型的准确性(图中Integrator为积分器)。
图4—16中的两条线分别是简化前的和简化后的,可以看出它们其实是非常接近的,这也就说明简化后的模型还是十分有效的。当然,我们不应该仅仅满足于现有的一个结论,应该在现有的基础上进行不断地思考和分析完善,这也告诉我们做科研应该是永不满足的一个过程,只有这样才能逐步提高,最后得到一个比较好的结果(图4—17)。
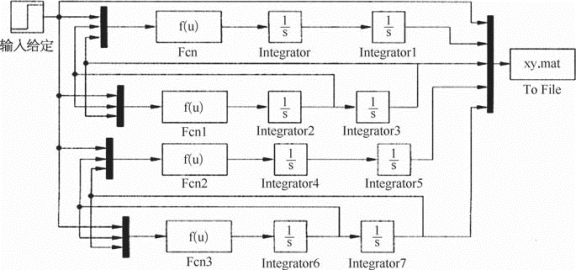
图4—15 Matlab模块操作界面
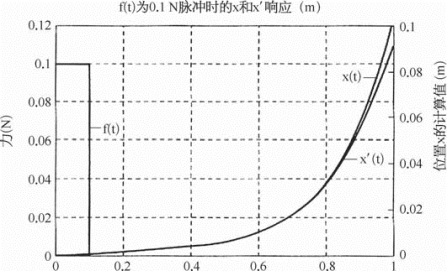
图4—16 模型的简化与验证(图片来自导师)
![]()
图4—17 学生体验的科研过程
在建立模型后,应该进行简化和验证,找到最优模型。对此,在接下来的工作中还会继续完善。在后面的工作中,我们会设计一套在施加轻微的扰动后能稳定,并且能适应可变参数的控制系统。以现有的结论为基础,对实验过程进行改进与完善,进一步认清研究对象的特点,制订下一步的科学研究技术路线,逐步提高。
