1.1.3 计算机的信息表示
1.数制
1)数制的基本概念
数制是指用一组固定的符号和统一的规则来表示数值的方法。按进位原则计数的方法称为进位计数制。人们普遍采用十进制,即逢十进一、借一当十,表示形式为123、(123)10或123D。计算机内部则采用二进制,即逢二进一、借一当二,表示形式为(10)2或10B。除此之外,常用的还有八进制,即逢八进一、借一当八,表示形式为(72)8或72O;十六进制,即逢十六进一、借一当十六,表示形式为(3A5B)16或3A5BH。
进位计数制由三大要素组成,即基数、数位和位权。
基数——所使用的数码个数,用R表示。二进制的基数为2,使用0和1这2个数码;八进制的基数为8,使用0至7这8个数码;十进制的基数为10,使用0~9这10个数码;十六进制的基数为16,使用0~9加上A~F,共16个数码。
数位——数码所处的位置。同一个数码因其位置不同,其大小也会有所不同。例如,十进制数22.2,整数部分从左至右,第1个数码2处在十位,表示20;第2个数码2处在个位,表示2;第3个数码2处在十分位,表示0.2。
位权——一个基数为底的幂值,每位数码的实际大小等于该数码乘以位权。例如,十进制整数的位权从低位到高位分别是100、101、102、103……;小数的位权从高位到低位分别是10-1、10-2、10-3……
4种进制数的特点见表1-1。
表1-1 4种进制数的特点
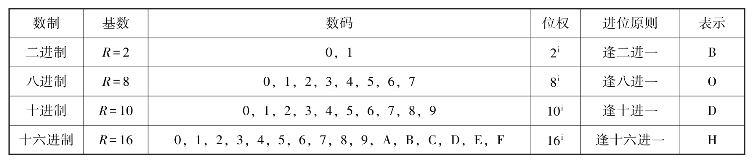

数制转换对照表格
2)数制之间的转换
非十进制数转换成十进制数。
将非十进制数转换成十进制数的方法为将该数的每位数码乘以各自对应的位权,然后将乘积求和。
【例1-1】将二进制数11011.01转换成十进制数。
(11011.01)2=1×24+1×23+0×22+1×21+1×20+0×2-1+1×2-2=(27.25)10

数制转换的计算
【例1-2】将八进制数73转换成十进制数。
(73)8=7×81+3×80=(59)10
【例1-3】将十六进制数5B转换成十进制数。
(5B)16=5×161+B×160=(91)10
十进制数转换成非十进制数。
将十进制数转换成非十进制数,要分别转换整数和小数,然后将两部分转换的结果连接起来。
整数部分的转换方法为“除R取余法”,即将十进制数除以R,得到商和余数,再将商继续除以R,得到新的商和余数,如此反复,直到商为0,然后将得到的余数,按照最后得到的余数为最高位,最先得到的余数为最低位依此排列,所得余数序列即为十进制整数对应的R进制整数。
小数部分的转换方法为“乘R取整法”,即将十进制数乘以R,取出积的整数部分后,剩下的小数部分再乘以R,如此反复,直到乘积为0或达到所要求的精度,然后将得到的整数,按照最先得到的整数为最高位,最后得到的整数为最低位依次排列,所得整数序列即为十进制小数对应的R进制小数。
【例1-4】将十进制数27.25转换成二进制数。

将整数部分和小数部分进行连接:(27.25)10=(11011.01)2
【例1-5】将十进制数59转换成八进制数。

(59)10=(73)8
【例1-6】将十进制数91转换成十六进制数。

(91)10=(5B)16
八进制数、十六进制数转换成二进制数。
八进制数转换成二进制数的方法为“一分为三”法,即将每一位八进制数码转换成三位二进制数码。
【例1-7】将八进制数76.25转换成二进制数。
八进制数 7 6 .2 5
二进制数111 110.010 101
(76.25)8=(111110.010101)2(https://www.daowen.com)
十六进制数转换成二进制数的方法为“一分为四”法,即将每一位十六进制数码转换成四位二进制数码。
【例1-8】将十六进制数2C.3D转换成二进制数。
十六进制数 2 C . 3 D
二进制数 0010 1100.0011 1101
(2C.3D)8=(101100.00111101)2
二进制数转换成八进制数、十六进制数。
二进制数转换成八进制数的方法为“三位分一组”法,即以小数点为基准,整数部分从右向左每三位二进制数转换成一位八进制数,最后一组不足三位时,最高位前面补“0”;小数部分则从左向右每三位二进制数转换成一位八进制数,最后一组不足三位时,尾部用“0”补齐。
【例1-9】将二进制数111110.010101转换成八进制数。
二进制数111 110.010 101
八进制数 7 6 .2 5
(111110.010101)2=(76.25)8
【例1-10】将二进制数101100.00111101转换成十六进制数。
二进制数 0010 1100.0011 1101
十六进制数 2 C . 3 D
(101100.00111101)2=(2C.3D)8
2.计算机中的数据单位
计算机内部采用二进制的形式存储和处理各种类型的数据,在衡量和表示计算机的存储容量和处理速度时,通常会用到以下3种数据单位。
1)位
位(bit)是计算机中最小的数据单位,在计算机中,数据是由多个“0”和“1”二进制代码组成的,每个二进制代码称为一位。
2)字节
字节(Byte)是计算机中数据存储的基本单位,每8位二进制代码为1个字节,即1 Byte=8 bit。计算机的存储容量指能够包含的字节数,分别用B(字节)、KB(千字节)、MB(兆字节)、GB(吉字节)和TB(太字节)表示,它们之间的换算关系如下:
1 KB=1 024 B=210 B
1 MB=1 024 KB=220 B
1 GB=1 024 MB=230 B
1 TB=1 024 GB=240 B
3)字长
字长是衡量计算机性能的一项重要指标,是指计算机一次能够并行处理的二进制代码位数。字长越长,计算机的运算速度就越快,处理精度就越高。字长通常是字节的整数倍,有8位、16位、32位、64位和128位等。

编码
3.计算机中的信息编码
由输入设备接收的各种形式信息,都必须转换成二进制的形式,才能被计算机识别。因此,需要对数字、符号、字母、汉字、图像、语音等信息进行二进制编码。以下介绍常用的西文字符编码和中文字符编码。
1)西文字符编码
ASCII编码:ASCII编码是美国信息交换标准代码,适用于所有拉丁字母。ASCII码用7位二进制数来表示包括数字、大小写字母、符号在内的128个不同的字符。
Unicode编码:Unicode编码是采用两个字码编码的国际标准编码,能够表示用于计算机通信的文字和相关符号。
2)中文字符编码
中文字符即汉字,比西文字符复杂得多,中文字符编码需要从汉字的输入、内部表示、输出等对汉字进行不同的编码。
汉字输入码:汉字输入码是用字母、数字和一些符号的组合对汉字进行编码,用于将汉字输入计算机,包括字音编码、字形编码、音形编码和数字编码。
汉字交换码:汉字交换码是具有汉字处理功能的不同的计算机系统之间进行汉字信息交换时所用的编码,包括区位码(GB2312)和国标码,区位码的字符集是一个94行(区)、94列(位)的方阵,国标码则是将区位码的十进制区号和位号分别转换成十六进制数,再分别加上20H。
汉字机内码:汉字机内码是指在计算机内部存储和处理所用的代码。汉字机内码是将汉字国标码的每个字节最高位加1,即汉字机内码=汉字国标码+8080H。
汉字字形码:汉字字形码是指用点阵的形式表示显示或打印输出汉字时产生的字形,对点阵中的每一个点用二进制进行编码,“0”和“1”分别表示“白”和“黑”。汉字字形码大多采用16×16点阵、32×32点阵、48×48点阵等,点阵密度越大,所占的字节就越大,汉字的输出质量就越好。
思政小知识
电子计算机二进制与中国太极八卦图有一定的相似之处。1667年,莱布尼茨在法国巴黎参观博物馆,看到了帕斯卡尔的一台加法机,引起了他要创造一台乘法机的兴趣。1701年秋末,正当54岁的莱布尼兹为创造乘法机冥思苦索、无路可走的时候,突然收到了他的法国传教士朋友(汉名白晋)从北京寄给他的“伏羲六十四卦次序图”和“伏羲六十四卦方位图”。莱布尼兹从这两张图中受到了很大启发,他发现,八卦是象形文字的雏形,由坤卦经艮、坎、巽、震、离、兑到乾卦,正是由0数到7,这样8个自然数所组成的完整的二进制数形。八卦中的“一”称为阳爻,相当于二进制中的“1”,而八卦中的“--”称为阴爻,相当于二进制中的“0”。六十四卦正是从0到63这64个自然数的完整的二进制数形。在数学中,八卦属于八阶矩阵。可见,中国古老的太极八卦图对电子计算机这门现代科学,具有历史性的贡献。
