5.2.3 构建PSWE模型
递进水盐嵌入神经网络(PSWE)通过HLSTM构造的编码器与BMLP构造解码器耦合所计算的损失,对整体模型进行协同更新,使整个PSWE神经网络模型能有效获取夏玉米的整个生长周期中的各项生长指标到土壤水盐动态变化,再从土壤水盐变化到产量、水利用率间的递进因果关系,以达到大幅提高预测精度的目的。
PSWE神经网络模型最终损失函数计算值为式(5.11)与式(5.13)的平均值,即

Huber Loss函数:一般农田水利模型中广泛采用的均方根误差(Root mean square error,RMSE)和均方误差(Mean square error,MSE)作为模型精度检验,但模型在拟合时存在对数据中的异常值进行敏感拟合,故并不适合数据分布并不平滑的农田水利数据。因此,本章采用Huber Loss函数(也称为平滑L1 Loss函数)进行损失计算。同时,为了增强递进神经网络的稳定性,本书同样采用Huber Loss函数作为目标函数来计算梯度并实时更新PSWE模型。
Huber Loss函数采用式(5.15)的分段定义,该函数本质上平衡了RMSE对异常值过于灵敏和平均绝对误差(MAE)对异常值的钝性,则
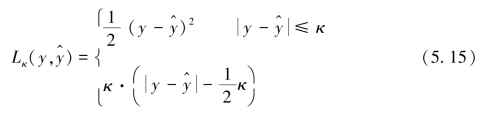
式中,κ起到平衡调节作用,当损失值小于κ时,Huber Loss函数会通过线性运算放大Loss的值;当Loss的值小于1时,Huber Loss可以通过二次方程来降低线性运算的损失。
目前,采用随机梯度下降(SGD)作为优化器的神经网络(如常用的BP神经网络)在峰值处梯度比较平缓,未立即收缩或减小,并且网络中所有参数的学习速率都是统一的。与上述模型不同的是,递进水盐嵌入神经网络模型PSWE在模型训练过程中收敛算法采用的是优化后的Adam优化算法[3]和Dropout算法进行耦合后的算法,使其能够更稳定、平滑地收敛。Adam优化算法的两个基本组成部分是动量项v和指数加权移动平均项s(也称为指数损失平均值),两者通常初始值均为零。动量项v累积梯度元g减小梯度方差计算为

其中,累积的梯度元为
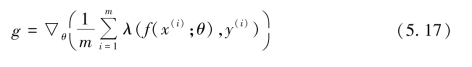
推导得

式中 t——迭代步长;
β——控制当前步长下降方向梯度的卷积,0≤β≤1。(https://www.daowen.com)
将指数加权移动平均项s的梯度方差累积以获得每个参数的学习速率,则
![]()
值得注意的是,由于v0和s0初始值均为0,造成大量的偏差主要倾向于小的值,为纠正这个问题,将vt和st重新归一化,使所有步骤各项值总和为1,此纠正称为偏差校正,即

类似有

通过对vt和st进行偏差校正,可对神经网络参数中各元素的梯度进行调整,即

式中 δ——预定义的学习速率;
ε——数值稳定化且非常小的常数。
参数更新为

至此,整个基于深度学习的递进水盐嵌入神经网络模型(PSWE)建立完成[4],此时可以根据HLSTM构造的编码器与BMLP构造的解码器中获取的2层递进因果关系进行迭代更新,对土壤水盐动态变化及作物生产效益进行模拟与预测。PSWE神经网络模型架构示意图如图5.3所示。
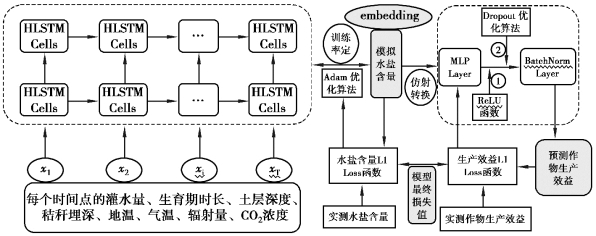
图5.3 递进水盐嵌入神经网络架构示意图
