附 录
构建递进水盐嵌入神经网络模型(PSWE)所用的数学算法:
附录1 激活函数
将非线性函数引入神经网络中,使神经网络能依据输入流的分布较为随机的逼近真实的复杂函数。当无激活函数时,线性函数关系使多层架构相当于单层模型。然而,目前许多研究均未正确地采用激活函数,大部分模型中采用S型函数作为激活函数,往往不能得到最优解。下面将说明S型函数不适用于农业水土工程的原因,并将直线整流函数(Rectified Linear Unit,ReLU)引入所提出的递进水盐嵌入网络模型中。
S型激活函数又称物生长函数,数学表达式为

S型激活函数压缩变化的数值范围在0~1,这往往导致神经网络饱和时,神经元梯度易为0(隐藏的神经元的梯度值趋于0或1时,均取0)。显然,饱和神经元的权重值参数无法及时更新。同时,梯度更新在这些连接的饱和神经元中传播缓慢,这种现象称为梯度消失。此外,如果将其应用到每一层上,e-x运算使S型函数计算成本很高,这也是现代深度学习架构弃用S型函数的另一个原因。而直线整流函数(ReLU)有效地解决上述问题。ReLU函数其表达式为
![]()
当x<0时,ReLU函数输出为零,否则x保持原始值,这样使整个神经网络的传播和收敛方式更有效。由于ReLU将神经元从限制的边界中解放出来,至少有一定数量的神经元在正区域进行反向传播,避免了梯度消失的问题。本书将ReLU应用于每一隐层并进行非线性变换,计算式为

附录2 批处理标准化BMLP
下面将如何对学习到的隐层表示进行标准化的批处理进行详细说明。当深度神经网络从深度架构中获得较好的泛化能力时,输入的数据在神经网络中各层的学习参数转换的过程中,也使模型训练变得更加复杂。在这种情况下,随着网络结构的加深(即层数的增加),架构中这些参数的微小变化将被放大。由于每一层输入分布的移位,要求后续的各层输入不断服从新的分布规则,极大地削弱了模型训练过程的稳定性,也削弱了模型本身的稳定性。考虑文中使用的六层PPN模型同样会遇到上述问题,本书利用标准化批处理来增强训练迭代,增强模型的稳定性。标准化批处理运算分为以下4步:
①给定一个最小的批处理B,得到B中所有元素的均值,即

式中 m——批处理的样本数量。
②采用各批次处理的平均值,计算对应方差,即

③标准化批处理操作可用样本批次的均值和方差表示,即

式中 ε——很小的值,但不等于0。
④通过两个可学习的参数对标准化批处理隐层进行缩放和移位,即

式中 γ,β——缩放和移位的参数,通过模型训练得到的,用来提高网络模型的表达能力。
批量标准化转换建模算法如下:
要求:
![]()
其中,l为数据层级;m为小批量样本的数量;γ为尺度参数,可学习;β为移位参数,可学习输出
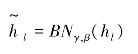
①l=1,2,3,…,L。
②更新最小批量样本平均值
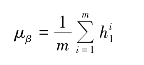
③更新最小批量样本方差
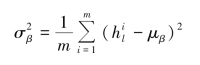
④最小批量样本隐层规范化
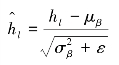
⑤标准化批处理隐层缩放和移位
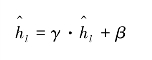
⑥结束。
附录3 Adam算法优化
要求:B={x1,…,xm},各个x对应相应的y值。
其中,m为小批量样本的数量;T为运算的迭代步数;v为动量项;s为指数损失平均值;βv为动量项的非负超参数;βs为指数损失平均值的非负超参数;ε是个很小的值,但不等于0。
初始化:v=0,s=0。(https://www.daowen.com)
①t=0,1,2,…,T。
②生成累积梯度
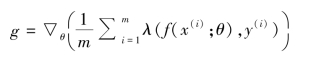
③t=t+1。
④动量项运算
![]()
⑤指数损失平均值运算
![]()
⑥动量项的偏差修正
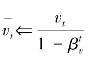
⑦指数损失平均值项偏差修正
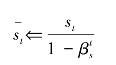
⑧重新调试梯度
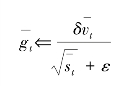
⑨更新参数
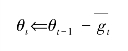
⑩结束。
附录4 Dropout算法优化
在模型训练数据集有限的情况下,深度复杂的网络结构通常会导致网络在训练过程中对输入的数据进行强行过度拟合,则称为过拟合或协同适应。Dropout是一种计算成本低(计算复杂度为O(n))且可有效地解决模型训练数据有限的算法,它通过每次训练随机迭代出暂时闲置非线性模型中的非输出神经元。具体来说,Dropout算法是对二进制掩码进行采样,将网络中输入和隐藏层生成结果相乘,并在训练迭代中暂时剔除输出值为0的元素。由于二进制掩码的采样是相互独立的,采样值为1的概率是整个神经网络的一个预定义超参数,Dropout的层级计算表达式为
![]()
式中 ☉——各元素点乘运算;
dl-1——Dropout算法中第l-1层掩码;
p——模型训练前的预定义超参数。
附录5 递进水盐嵌入神经网络模型(PSWE)的算法
要求:Bx={x1,…,xm}:小批量的训练数据组。
其中,L为数据层数;m为小批量样本数量。
①迭代次数t=1,2,3,…,T。
②从训练数据组中抽取m个样本(Bx),并得到相应的yi。
③l=1,2,3,…,L。
④按照正文中,式(7-12)
![]()
⑤按照式(附-3)
![]()
⑥按照式(附-8)hl=(hl-1☉dl-1)TWl+bl;d~Bernoulli(p)进行Dropout运算。
⑦按照式(附-4)—式(附-7)对数据进行批处理归一化,即
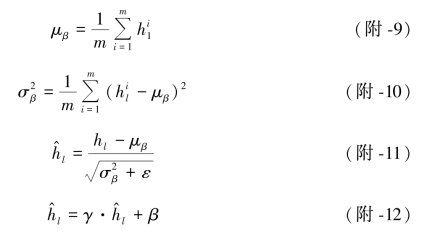
⑧结束。
⑨根据式
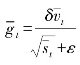
⑩结束。
⑪根据模拟结果,决定是否返回到y′。
