二、基本运算电路

二、基本运算电路

1.反相输入运算放大器

如图4-13所示，R₁为外接输入电阻，R_f为跨接在输出端和反相输入端之间的反馈元件，R₂为平衡电阻。适当选择R₂的值（一般应使R₂=R₁∥R_f），可使两个输入端外接电阻相等，使理想运算放大电路处于平衡状态；输入信号u_i经R₁从反相端输入，同相端经R₂接地。

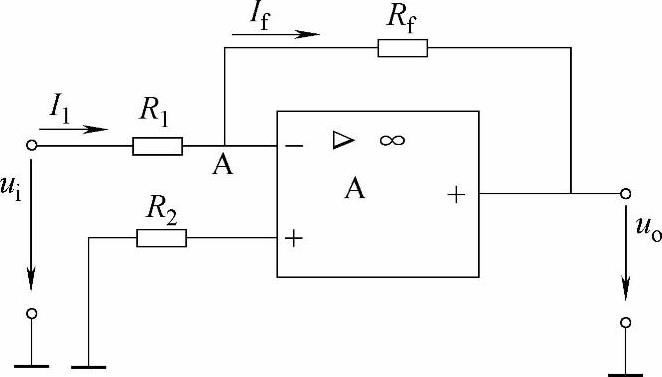
图4-13 反相输入运算放大器

由理想运算放大器的两个重要特点可知，流入放大器本身的电流近似为零，故R2上无电压降，U₊≈0，而U₊=U_-，因此U_-≈0，U_-=U_A，我们可以认为UA接近于地电位而又不是真正的地电位，因此常称A点为“虚地”，即

式（4-2）表示，在理想条件下，反馈电流I_f与输入电流I₁相等。虚地点的存在是反相输入放大器的重要特征。

图4-13中，因U_A≈0，I₁≈I_f，故有

U_o=-I_fRf

U_i=I₁R₁

由此可求得反相输入放大器的电压放大倍数为

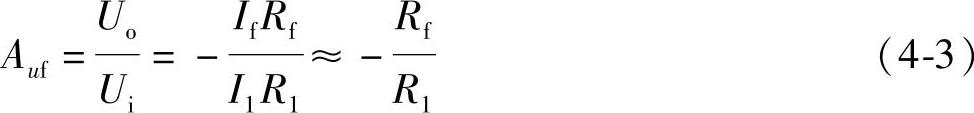
式中负号表示输出电压U_o与输入电压U_i反相，且U_o与U_i的关系只取决于R_f和R₁的比值，与集成运放的参数无关。

例4-1 图4-13中，若R₁=1kΩ，R_f=36kΩ，U_i=0.1V。试求：A_uf、U_o及R₂的值。

解 由式（4-3）得

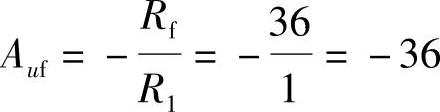
输出电压U_o为

U_o=A_ufU_i=-36×0.1V=-3.6V

平衡电阻R₂为

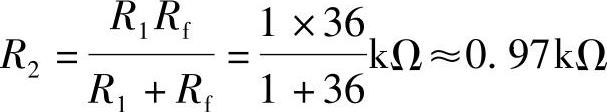
2.同相输入运算放大器

如图4-14所示，信号由同相输入端加入，R_f、R₂与反相输入放大器中的接法及作用相同。为保持输入端平衡，仍应使R₂=R₁∥R_f。

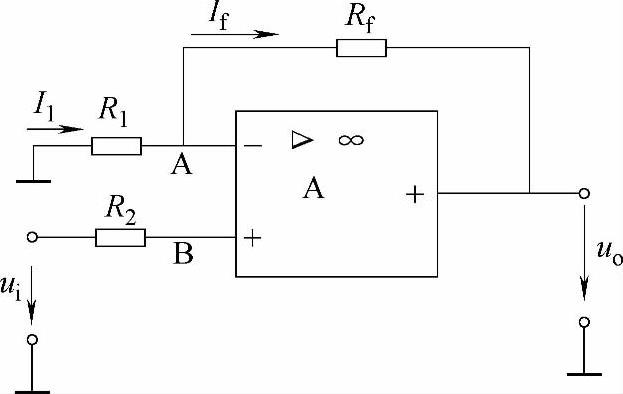
图4-14 同相输入运算放大器

根据理想运算放大器的两个重要特点可知，流入放大器的净输入电流为零，则U_i=U₊，又因U_-≈U₊，所以U_-≈U_i。也就是说，两个输入端对“地”电压都近似为输入电压，“+”和“-”两端出现“虚假短路”现象。“虚假短路”的端点间不仅电压为零，而且电流也为零，这是同相输入放大器的重要特征。

根据理想放大器的两个重要特点及“虚假短路”概念可知：

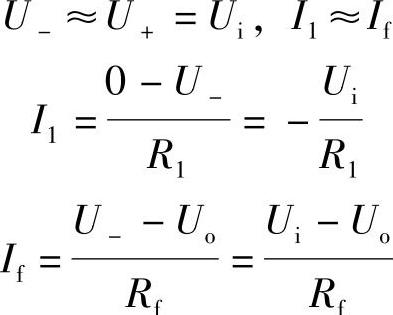
则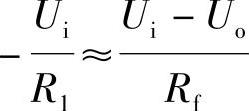

即

由式（4-4）可求得同相输入运算放大器的电压放大倍数，即

式（4-5）表明：理想的同相输入运算放大器，输入电压u_i与输出电压u_o相位相同，且u_o与u_i的关系只与R₁和R_f的值有关，与理想运算放大器的参数无关。

例4-2 试求图4-15所示电路的输出电压u_o与输入电压u_i之间的关系。

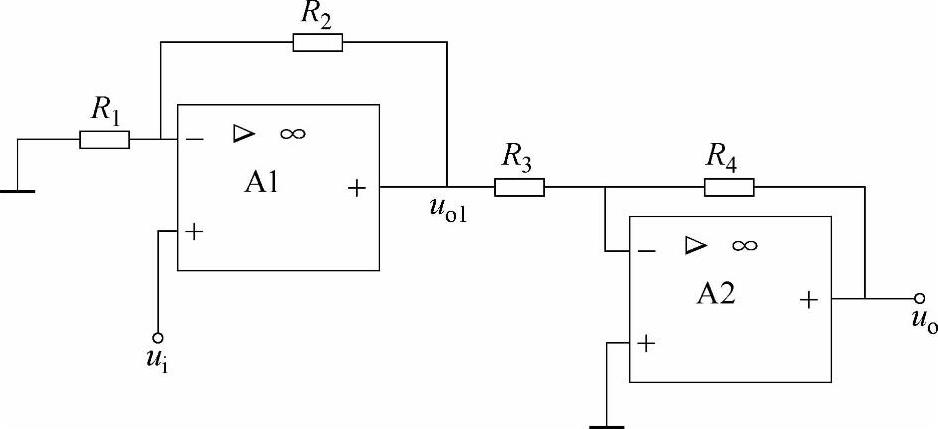
图4-15 例4-2图

解 分析电路可知，它是由一个同相输入运算放大器和一个反相输入运算放大器串联而成，输入信号u_i加在同相输入端，经A1放大后，输出一个与u_i同相的u_o1，u_o1作为反相输入运算放大器的输入信号，经A2再次放大后输出u_o，u_o与u_o1由式（4-3）、式（4-5）得

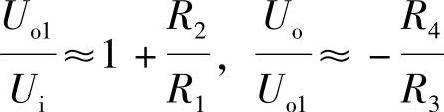
即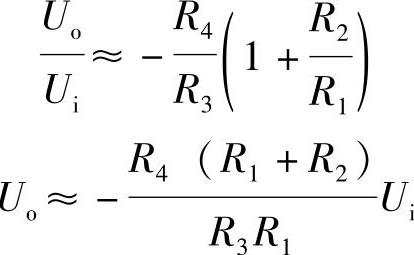

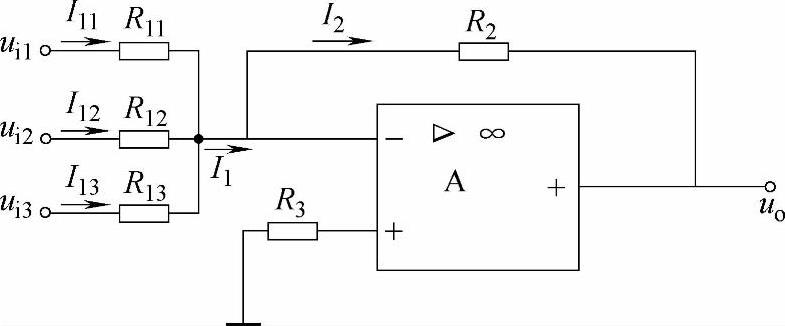
图4-16 加法运算放大器

3.加法运算放大器

如图4-16所示，该电路在反相输入运算放大器的基础上又多加了几个输入端。它有三个输入信号U_i1、U_i2、U_i3，它们均从反相输入端输入，同相输入端经过平衡电阻R₃接地，输出信号u_o经反馈电阻R₂送回到反相输入端，以实现负反馈。利用“虚地”概念可得

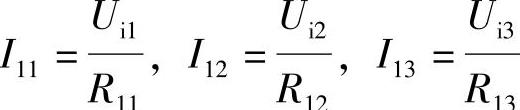
由于放大器的差模输入电阻无穷大，所以可以认为放大器的净输入电流近似为零，则有

又因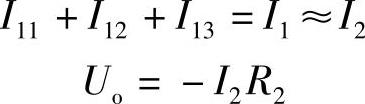

即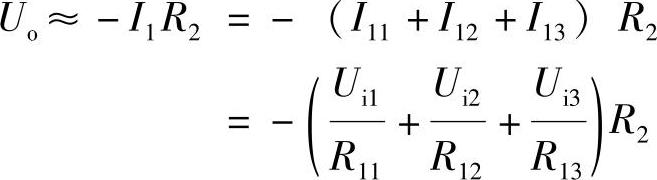

若各输入端的外接电阻均相等且为R，即

R₁₁=R₁₂=R₁₃=R

则有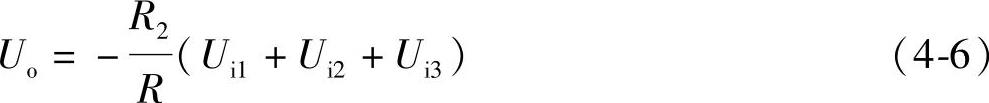

4.积分运算放大器

如图4-17所示，该电路是把反相输入运算放大器中的反馈电阻用电容C替代后而成的。

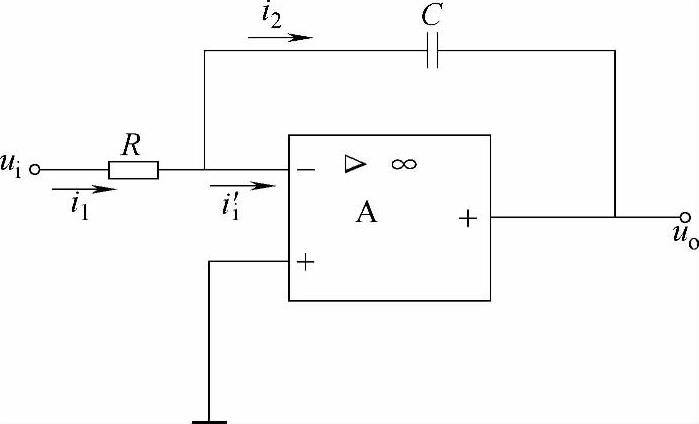
图4-17 积分运算放大器

根据电容的充电特性和规律可知，电容两端的电压u_C正比于电容充电电流i对时间t的积分，即

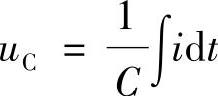
由图4-17可见，u_i是经R反相输入的，利用“虚地”概念，根据理想运算放大器的两个重要特点可知A_u很大，i_i′≈0，i₁≈i₂，则输入电压u_i为

u_i≈i₁R≈i₂R

输出电压u_o为

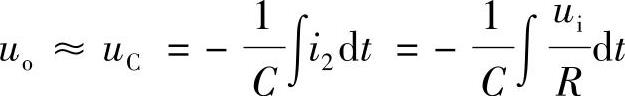
所以

当输入信号u_i为固定值U_i时，输出电压U_o为

式（4-7）说明输出电压和输入电压成积分关系且相位相反。式（4-8）说明，在输入电压为恒定值时，输出电压随时间而线性增长。

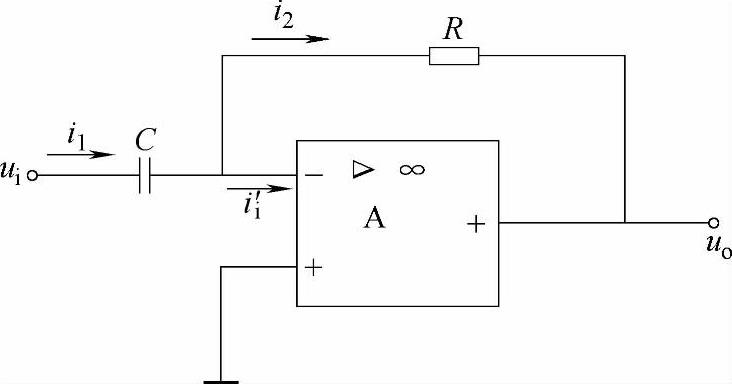
图4-18 微分运算放大器

5.微分运算放大器

如图4-18所示，该电路是将积分运算放大器中的电阻R和电容C调换位置而成的。信号u_i经电容C加到放大器的反相输入端，且电容C的充电电流i正比于电容电压u_C对时间的导数，即

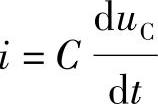
利用“虚地”概念，根据理想运算放大器的特点，因A_u很大，i_i′≈0，i₁≈i₂，则

u_i≈u_C

u_o≈i₂R≈-i₁R

由于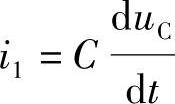

则

式（4-9）说明了输出电压和输入电压成微分关系且相位相反。

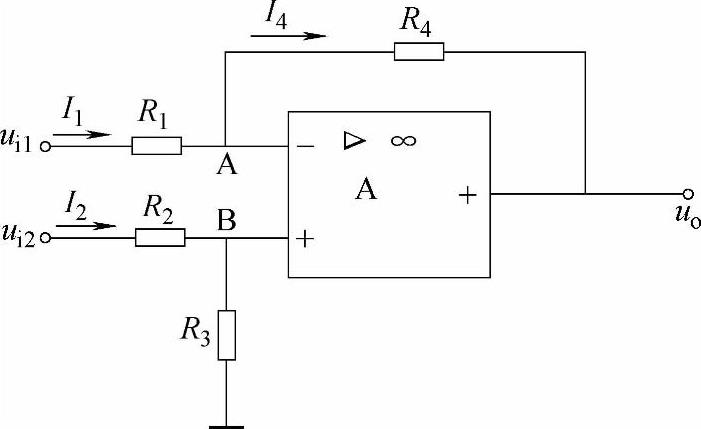
图4-19 减法运算放大器

6.减法运算放大器

如图4-19所示，该电路由反相输入和同相输入两种运算放大器组合而成。反相输入信号u_i1经电阻R₁加到反相输入端，同相输入信号u_i2经电阻R₂和R₃分压后加到同相输入端。根据运算放大器的特点得出，I₁=I₄，即

又因

式（4-10）和式（4-11）联立，可求得U_o，即

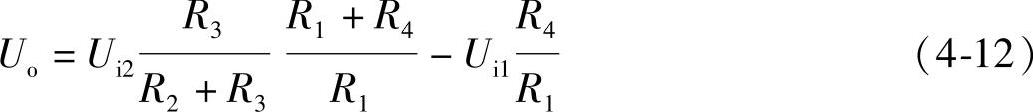
若使R₂=R₁，R₃=R₄，则式（4-12）可写成

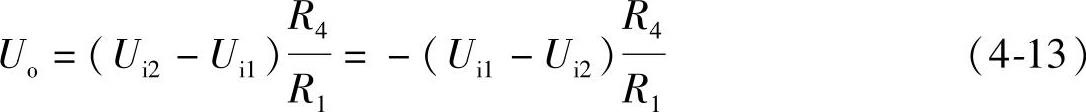
式（4-13）表明了输出电压U_o与两个输入电压U_i1和U_i2之差成正比，即电路实现了减法运算。