2.1.1 太阳光压力推进理论研究
1.太阳辐射压力的物理解释
太阳帆航天器的推进力来自太阳与太阳帆帆面之间辐射能量的动量交换。太阳帆推进技术在物理机制上是成熟的,从量子力学角度看,可以将辐射压力看作是光子动量的传送,从光的电磁描述角度,可以认为光是通过电磁波运送动量到太阳帆上。图2-1所示为太阳帆推进原理示意图。
使用量子力学理论,可将辐射压力看作由于光子动量的传送组成光的能量量子群。根据普朗克定律,一个频率为υ的光子,输送能量E为
![]()
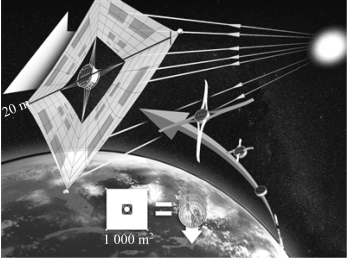
图2-1 太阳帆推进原理示意图
式中,h是普朗克常数。除了量子角度,狭义相对论的质量能量守恒使得移动物体能量可为
![]()
式中,m0是静止质量,p是动量,c是光速。方程第一项表示物体静止能量,第二项表示由运动产生的能量。既然光子静止能量为零,它的能量可写为
![]()
使用式(2-1)、式(2-3)定义的光子能量,单个光子的动量输送可写为
![]()
需要注意的是要联合使用量子力学和经典物理理论的狭义相对论才能推得这个方程。为了计算施加在物体上的压力,必须考虑一簇光子输送的动量。距离太阳距离为r的能量簇W(单位时间单位面积的能量穿越)可按照太阳光度LS予以写出,由日地距离RE缩放为


式中,WE是距日1 AU地球处的能量通量。使用式(2-5)和式(2-6),可给出Δt时间内能量ΔE横跨面积A垂直入射辐射的输送
![]()
从方程式(2-3)这个能量输送动量Δp,由下式给出:
![]()
施加在表面的压力p为单位时间单位面积输送的动量,以至于

因此,使用方程式(2-7),由于光子动量输送施加在表面的压力由下式给出

对于一个理想反射表面观测到的压力是方程式(2-10)提供的2倍,这是由于入射反射。使用式(2-10),在距日1 AU处,施加在太阳帆上的太阳辐射压力现在可以计算。WE的一个可以接受的平均值是1 368 J/(S·m2)。因此,1 AU处施加在理想反射太阳帆上的压力是9.12×10-6 N/m2。
2.太阳帆航天器推进能力的描述方式
为了描述太阳帆的推进能力,国际上通过三种指标进行推进能力的描述:一是太阳帆探测器特征加速度a,指太阳帆探测器在距离太阳1 AU时所受的太阳辐射加速度;二是光压因子β,指太阳光垂直照射帆面有效面积(S)时产生的光压力与太阳对探测器的引力之间的比值;三是质量面积比m/S,指探测器的总质量(m)与帆面有效面积的比值。
光压因子仅与质量面积比有关,两者之间成反比关系,系数是1.53 g/m2,特征加速度是通过太阳光压常数除以质量面积比获得的,光压常数是9.12×10-6 N·m-2。由下述公式表示:
光压因子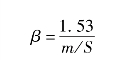
特征加速度![]()
可以发现上述三种指标虽然表征不同,但是内涵都是一致的,核心就是面积质量比(面密度),也是表征太阳帆性能的最重要指标,因此对于给定面密度的太阳帆,光压力与引力的比值为常数,用β表示,称为光压因子。光压因子只与太阳帆的面密度有关,β值越大,说明太阳帆越轻,性能越优良。如果光压力与引力相同,则可以得到太阳帆面密度称为临界面密度,数值上等于1.53 g/m2。以正方形帆为例,可以得到在不同加速度下太阳帆探测器质量与帆面尺寸之间的关系,如图2-2所示。
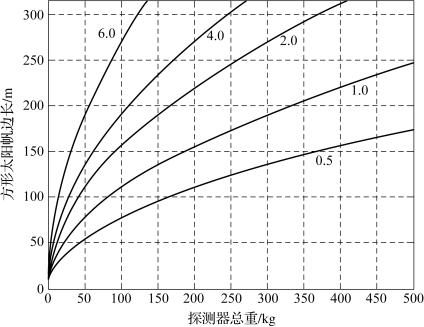
图2-2 探测器质量与帆面尺寸的关系图
图中描述了加速度从0.5 mm/s2到6 mm/s2时,探测器总重500 kg以内的方形帆尺寸。可以看到100 kg的探测器需要的帆面积从数千平方米到数万平方米。
3.太阳帆航天器的基本轨道动力学和典型轨道特性
1)推力方式比较
首先分析了常规推进、电推进和太阳帆推进方式的优劣与任务周期的关系。如果考虑初始质量为最终质量的3倍,可以得到不同加速度情况下的任务时间与Isp之间的关系曲线,如图2-3所示,加速度从0.5 mm/s2到6.5 mm/s2。
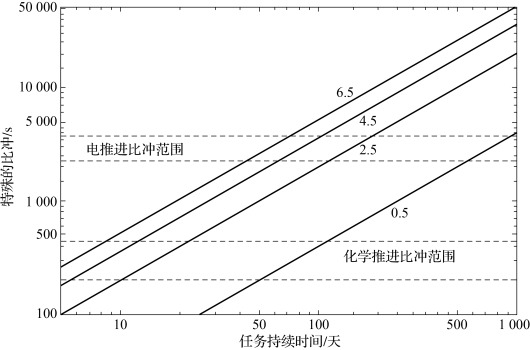
图2-3 太阳帆推进与任务周期的关系
化学推进的比冲范围约为从200 s到450 s,电推进的比冲范围约为从2 200 s到3 700 s,从图中可以看出随着任务时间的增长,太阳帆的优势逐渐明显,即使是大比冲的电推进器只要任务周期达到两年半以上,太阳帆都可以认为具有优势。
2)轨道动力学模型及特征分析
进而建立了太阳帆推进的轨道动力学模型并开展了轨道特性分析。太阳帆处于空间不同位置,不同的天体对其引力大小不同,根据太阳帆受到天体的引力的量级,可以考虑主要天体的引力。当太阳帆远离所有天体时,可以只考虑太阳引力。当太阳帆在围绕某个天体运动时,可以只考虑该天体的引力。当天体在某两个主天体形成的限制性三体问题的平动点附近时,需要同时考虑这两个主天体的引力。
太阳帆早期的经典研究都集中在日心轨道,日心轨道动力学可以在不同的坐标系下进行描述。在日心惯性坐标系下,太阳帆的动力学方程可以表示为
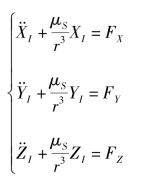
在球坐标系下,定义ϕ为r与黄道面之间的夹角,ψ为r在黄道面的投影与XI的夹角,如图2-4所示,在球坐标系下的动力学方程可以表示为
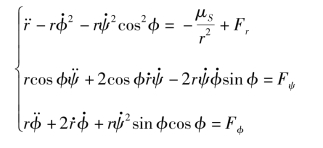
轨道坐标系由位置单位矢量er、轨道面法向单位矢量eh以及横向单位矢量et形成右手坐标系,如图2-5所示,在轨道坐标系下的动力学方程可以表示为
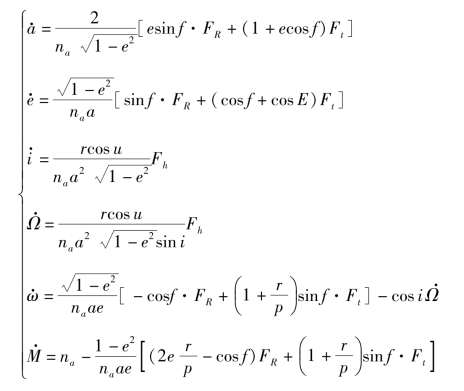
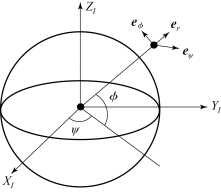
图2-4 球坐标系的描述
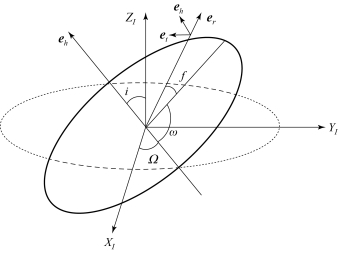
图2-5 轨道坐标系的描述
太阳帆的位置矢量在不同的坐标系的投影之间可以相互转换,惯性系到球坐标系的转换可以描述为
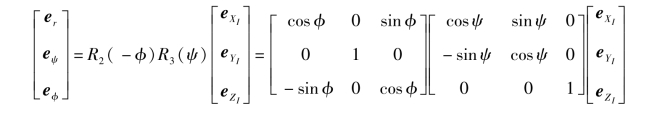
惯性坐标系到轨道坐标系的转换可以表示为
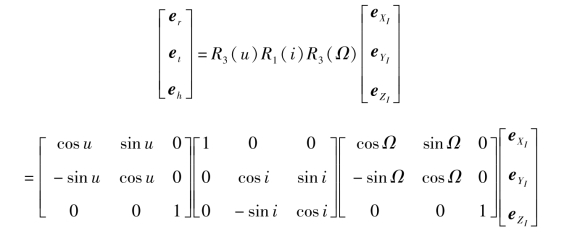
Gauss形式太阳帆的轨道动力学模型:
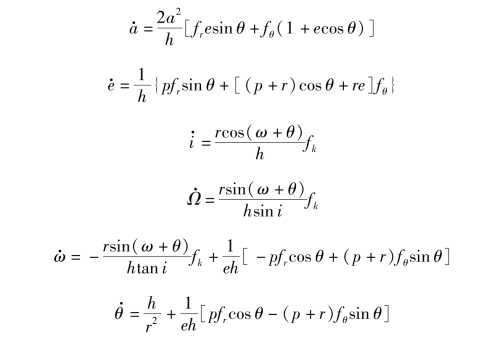
拉格朗日微分形式太阳帆的轨道动力学模型:
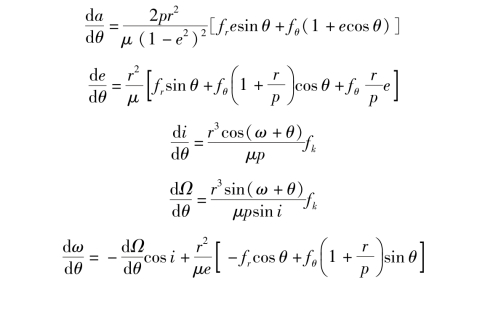 (https://www.daowen.com)
(https://www.daowen.com)
密切轨道六要素形式太阳帆的轨道动力学模型:
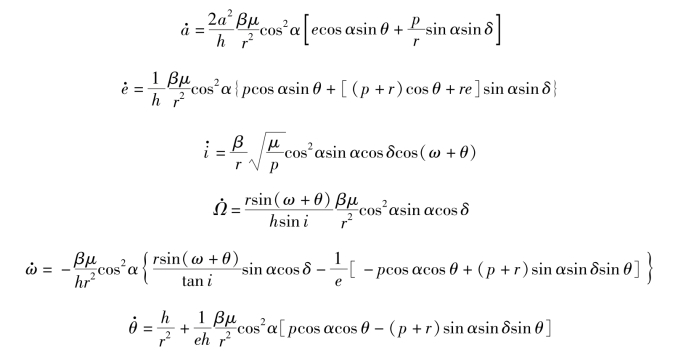
利用太阳帆在不同坐标系下的动力学方程的描述,可以研究太阳帆在日心轨道的动力学特征,包括星际转移轨道。二体模型下太阳帆的能量可以表示为
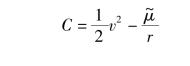
利用能量可以判断太阳帆的轨道类型:当C<0时,即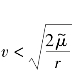 ,太阳帆的轨道为椭圆;当C=0时,即
,太阳帆的轨道为椭圆;当C=0时,即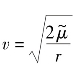 ,太阳帆的轨道为抛物线;当C>0时,即
,太阳帆的轨道为抛物线;当C>0时,即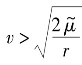 ,太阳帆的轨道为双曲线。
,太阳帆的轨道为双曲线。
当太阳帆的轨道为椭圆时,设h为太阳帆的角动量,则太阳帆到太阳的距离可以表示为
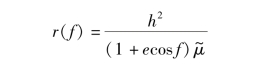
轨道速度大小可以表示为
![]()
轨道周期可以表示为
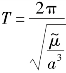
由上面的公式可知,当太阳帆与传统航天器在一个长半轴相同的日心轨道上运行时,太阳帆比传统航天器的周期长。当偏心率也相同时,太阳帆具有较小的动量矩,即在同一轨道运行时,太阳帆的日心速度比传统航天器小。如果航天器运行在一个半径为a的圆轨道上,将太阳帆展开,且太阳光压力沿径向施加,则太阳帆的轨道将发生改变,当β<1/2时,太阳帆的轨道将为椭圆轨道,椭圆轨道的长半轴为
![]()
从上述结果可以看出,当β=1时,偏心率![]() 很容易理解,β=1意味着太阳对太阳帆的引力和光压力抵消,因此,太阳帆受到的合外力为零,太阳帆将做直线运动;当β=1/2时,偏心率
很容易理解,β=1意味着太阳对太阳帆的引力和光压力抵消,因此,太阳帆受到的合外力为零,太阳帆将做直线运动;当β=1/2时,偏心率![]() ,太阳帆的轨道为抛物线;当β<1/2时,偏心率
,太阳帆的轨道为抛物线;当β<1/2时,偏心率![]() ,太阳帆的轨道为椭圆;当1/2<β<1时,偏心率
,太阳帆的轨道为椭圆;当1/2<β<1时,偏心率![]() ,太阳帆的轨道为双曲线;当β>1时,太阳引力和太阳光压力的合力所产生的效果相当于正引力势场,太阳帆的轨道将为双曲线,但是将沿远离太阳的方向运动。
,太阳帆的轨道为双曲线;当β>1时,太阳引力和太阳光压力的合力所产生的效果相当于正引力势场,太阳帆的轨道将为双曲线,但是将沿远离太阳的方向运动。
3)特殊轨道类型特点分析
利用上述模型分析了日心轨道中的椭圆、双曲线、抛物线轨道的运行特点与光压因子的关系,分析了太阳帆在圆轨道、椭圆轨道、直线轨道、逃逸轨道以及对数螺旋轨道上运行的特点。针对行星中心轨道分析了利用太阳帆进行逃逸的情况。结合上述不同的轨道类型,分别进行了轨道的稳定性分析。
考虑太阳帆部署在半径为r圆日心轨道上,圆轨道速度![]() ,帆的法向沿着太阳光线方向。光压因子β=0,显然轨道是半径r的圆开普勒轨道。光压因子范围在0<β<1/2,太阳帆将比局部圆轨道速度
,帆的法向沿着太阳光线方向。光压因子β=0,显然轨道是半径r的圆开普勒轨道。光压因子范围在0<β<1/2,太阳帆将比局部圆轨道速度![]() 快,以至于轨道是椭圆的。对于光压因子β=0.5,太阳帆以逃逸速度移动,因此沿着抛物线轨道移动。类似地,光压因子范围在1/2<β<1,太阳帆将沿着双曲线轨道移动。对于光压因子为1的轨道,太阳光压力精确地平衡太阳重力以至于太阳帆以速度
快,以至于轨道是椭圆的。对于光压因子β=0.5,太阳帆以逃逸速度移动,因此沿着抛物线轨道移动。类似地,光压因子范围在1/2<β<1,太阳帆将沿着双曲线轨道移动。对于光压因子为1的轨道,太阳光压力精确地平衡太阳重力以至于太阳帆以速度![]() 沿着直线轨道运动。最后,对于大于1的光压因子,实际在帆上的有效力改变了正负符号,同样太阳帆沿着双曲轨道移动,但是力的方向相反了。
沿着直线轨道运动。最后,对于大于1的光压因子,实际在帆上的有效力改变了正负符号,同样太阳帆沿着双曲轨道移动,但是力的方向相反了。
圆轨道(e=0)
对于圆轨道,太阳帆轨道周期是轨道半径和太阳帆光压因子的函数:
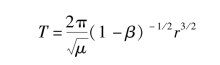
以至于太阳帆轨道周期与它的轨道半径解耦了。通过恰当地选择太阳帆光压因子,可以任意选择太阳帆周期在以下的约束以内:
![]()
为了在某些需要的数值上同步太阳帆轨道周期,半径r处所需的太阳帆光压因子选为
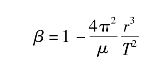
椭圆轨道(0<e<1)
对于椭圆轨道,开普勒轨道的关系将再次适用,但是需要进行修正万有引力参数。太阳帆部署在轨道后所得的日心轨道半长轴和偏心率由下式给出:
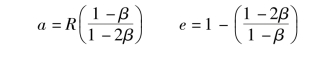
可见轨道偏心率与初始圆轨道半径无关。
椭圆轨道的使用同样提供了霍曼类型转移的机会,但是仅仅使用单脉冲。太阳帆转移可提供显著减少的Δv,但是代价是转移时间的增长,太阳帆转移时间TS总是比霍曼转移时间TH长。这个Δv的缩减当然与所需的太阳帆质量抵消了。
直线轨道
如果选择太阳帆光压因子是β=1,将没有净力施加在太阳帆上。太阳帆将完全移除太阳万有引力影响。既然太阳光压力和太阳万有引力均是反比二次方规律,太阳帆可在任何位置相对于太阳静止。另外,如果太阳帆相对于太阳有初始速度,它将以恒定的速度沿着直线轨道运行。下式给出速度和线性距离:
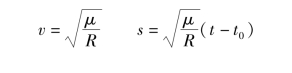
逃逸轨道(e≥1)
直接通过选择太阳帆光压因子来进行逃逸轨道是可行的,β=0.5提供了抛物线逃逸。太阳帆光压因子大于1,将得到双曲轨道族。这种情况下,施加在太阳帆上有效的力遵循反比二次方规律,但是力是径向向外的,远离太阳。既然有效的力是反比二次方的,则轨道是圆锥段的。对于光压因子大于1的太阳帆,双曲轨道反转以至于太阳占据了圆锥段的相反的焦点。
对数螺旋轨道
产生对数螺旋轨道需要航天器推进产生的加速度有与轨道半径二次方成反比的变量。太阳帆满足这种情况,对数螺旋轨道对于星际转移是一个很具有吸引力的选择。另外,既然帆的姿态相对于太阳光线必须是固定的,仅需要一个简单的制导律。对数螺旋轨道的一个主要的特点是太阳帆速度矢量相对于瞬时半径矢量在整个转移中保持固定的角。这个轨道特点导致星际转移中对数螺旋轨道应用起来很困难。对于圆轨道之间的转移,初始和最终太阳帆速度矢量将与初始和最终轨道不匹配。
行星中心轨道
上面已经讨论了日心太阳帆轨道,下面将考虑行星中心太阳帆轨道。行星中心理想反射太阳帆的一般运动方程为
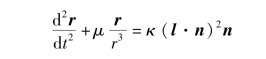
此处参数κ是太阳帆加速度的幅值,l是沿着太阳光线的单位矢量。对于地心轨道,κ是太阳帆特征加速度。行星中心轨道主要考虑的是利用太阳帆进行轨道逃逸,由于地球轨道的万有引力,逃逸轨道需要长时间的螺旋,需要快速的太阳帆旋转速率。对于这些原因,地球逃逸轨道事实上最好避免。
次最优轨道
考虑的轨道机动的第一个方法是简单地使用帆俯仰角的太阳光压力的开关转换。在太阳帆轨道的一半,太阳帆将面对太阳,而在轨道另一半,太阳帆将边缘对着太阳。尽管开关的形式很简单,在单位轨道期间需要两次快速的90°旋转机动操作。旋转持续时间相对于轨道周期必须是短的,以避免效率的损失。在次优轨道控制中,设计了轨道速率制导、局部最优制导以及避免快速旋转的极轨逃逸策略。
最小时间逃逸轨道
使用最优控制理论,研究了时间最优逃逸轨道。通过在整个轨道周期内平均变量方程,可去除短周期项,导致所需时间的显著减少。行星逃逸帆制导律的任何选择,无论是最优还是次最优,最大帆旋转角速度将是确定轨道效率的限制因素。具有低旋转角速度的太阳帆在每个轨道周期内向着太阳的弧段期间不能够再次快速地调整姿态以适应最优俯仰角。通过使用双面均可反射的帆薄膜,可以消除这些快速旋转机动。然而,质量节约通过允许小姿态作动器的使用而达到目的,而质量节约必须折中以预备额外的由帆涂层增加的质量。长逃逸螺旋通过使用化学推进将太阳帆直接注入星际轨道而可以避免。
近似逃逸时间
尽管以恰当的太阳帆制导律通过太阳帆运动方程数值积分,可容易地得到从某初始轨道算起的逃逸时间,但是为逃逸时间推导恰当的表达式是很有用的。考虑局部最优制导律,近似的逃逸时间为
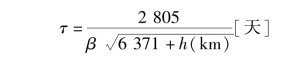
此处h是初始轨道高度,β是通常的太阳帆光压因子。能够发现逃逸时间是开始轨道姿态的强函数,因此太阳帆最好直接从地球逃逸轨道开始任务,或至少从地球静止轨道开始任务。
哈密尔顿-雅可比方法的解
通过使用哈密尔顿-雅可比理论研究行星中心太阳帆轨道动力学,证明对于固定姿态和一个(假设)固定太阳光线的太阳帆,存在一般的、封闭形式的解析解。
按照雅可比椭圆函数得到封闭的解如下:
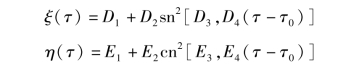
此处Di,Ei(i=1~4)和τ0是运动的常数,通过正则常数αj(j=1,2,3)定义。
通过上述研究和分析得出如下结论:
通过选择合适的光压因子和到太阳的距离,可以获得包括直线轨道在内的一系列极具特点的轨道,虽然比霍曼转移的效率要低,但是更适合于太阳同步、太阳风空间变化等特性。
从稳定性的角度看,太阳帆有些极具特点的轨道包括悬浮轨道是不稳定的,但是不稳定量程都比较长,可以以年来计算,因此在施加主动控制时可以充分利用其特点。
低的光压因子必然要伴随着长期转移时间,因此太阳帆的实用性取决于探测器性能和任务周期,太阳帆更适用于周期较长的任务。
利用太阳帆开展行星逃逸需要长时间的螺旋上升,还需要太阳帆具有快速的旋转速率,因此不建议纯粹利用太阳帆推进来逃逸,最好直接进入星际转移轨道。
