4.4.2 太阳帆面展开技术研究
1.帆面展开技术要求
为使太阳帆面能顺利展开,展开方式简单可靠,展开过程对其他机构及帆面造成的影响较小,对有支撑臂的方形帆展开过程的整体要求进行了分析。对帆面薄膜展开过程要求主要包括以下方面:
(1)帆面能在支撑臂拉力作用下顺利展开,不出现帆面缠结现象,并且展开过程有序;
(2)帆面展开过程稳定,尽量不出现抖动或抖动幅度较小,易于控制;
(3)展开对帆面影响小,展开过程中整个帆面出现明显的应力集中区域越小越好,不会导致帆面撕裂等现象出现;
(4)由于帆面折叠产生折痕,导致帆面不可能完全展平,在帆面最大应力没达到帆面屈服应力之前,帆面展开的程度越大越好。
2.帆面展开过程数值模拟
本节利用ANSYS/LS-DYNA软件对采用叶内折叠、叶外折叠及斜叶外折叠三种折叠方式薄膜的展开过程进行有限元仿真,分析其仿真结果,进一步对三种折叠方式进行比较。
•有限元模型
材料选择为聚酰亚胺薄膜Kapton,薄膜性能参数列于表4-20中。由于模型计算时需考虑材料的塑性变形,材料类型选择为双线性各向同性材料。建立边长为12 m的方形薄膜折叠结构的有限元模型,为了方便建模,设定相邻薄膜间隔为1 mm。
表4-20 材料属性

对三种折叠方式分为两个对比组来进行仿真建模:
(1)第一组仅建立叶内折叠结构薄膜的有限元模型,设置两个不同的折叠宽度,比较不同折叠宽度对于折叠结构的影响,进行较细致的网格划分,最终生成的两个有限元模型如图4-62所示。

图4-62 第一组有限元模型
(2)第二组分别建立三种折叠结构薄膜的有限元模型,三种折叠结构取相同的折叠宽度,比较不同折叠结构展开过程,进行网格划分后的有限元模型示于图4-63。

图4-63 第二组有限元模型
为了便于比较,将两对比组的模型分别编号为模型1到模型5,每个模型所对应的折叠结构类型、折叠宽度、有限元模型生成节点数和单元数都列于表4-21中。
表4-21 有限元模型参数

续表
•定义载荷和接触
对节点施加力时,节点速度随时间变化不断增加,是一个加速的过程,而在太阳帆展开的过程中,理想状态下支撑臂伸展是以恒定速度伸出的。因此,仿真时在薄膜的四个角分别施加恒定的速度,方向沿着薄膜展开状态的对角线方向,以模拟支撑臂对薄膜的作用。每个角选取四个节点,防止单点施加载荷时可能会造成的沙漏变形。
运算时间通过计算帆面完全展开时顶点所经过的距离除以节点加速度得到。因此对于不同的折叠方式,甚至折叠宽度不同时,计算时间也会有差异。将两个对比组中帆面完全展开时顶点所经过的距离、节点处施加的速度的值以及每个模型的运算时间分别列于表4-22中。
表4-22 速度载荷施加参数
在ANSYS/LS-DYNA程序中没有接触单元,只要定义可能接触的接触表面、接触类型以及与接触有关的一些参数,在计算过程中程序就能保证接触界面不发生穿透,并在接触界面相对运动时考虑摩擦力的作用。接触类型主要包括单面接触、节点-表面接触和表面-表面接触几种。
对薄膜定义接触,选择自动单面接触,单面接触用于一个物体表面的自身接触或它与另一个物体表面接触,使用单面接触时,ANSYS/LS-DYNA将自动判定模型中哪处表面发生接触,不需要定义Contact和Target表面,并且当定义单面接触时,它允许一个模型的所有外边面都可能发生接触,这对于预先不知道接触表面的自身接触或大变形问题非常有用。
•边界条件和求解设置
用ANSYS进行计算时,需要对薄膜施加一定的约束。结合实际帆面展开时施加约束的情况,帆面的四个顶点由于与支撑臂相连接,是固定在XY平面内的,且顶点的三个转动自由度都被限制。因此,在四个顶点处对Z轴方向进行约束,同时约束三个转动自由度。在实际情况中,帆面中心点应固定在四个支撑臂根部交会的中心,但是考虑不同的折叠方式,帆面不能固定在原点处。因而对薄膜中心点施加X轴方向和Y轴方向的约束,Z轴方向自由,并且约束X轴方向和Y轴方向的转动自由度,Z轴方向转动自由。两组中各有限元模型施加约束的情况如图4-64、图4-65所示。
图4-64 第一组施加载荷和约束的有限元模型

图4-65 第二组施加载荷和约束的有限元模型
根据表4-22中计算得出的施加载荷的时间来设置计算终止时间,使二者相等。设置时间步长的质量缩放为1×10-5,质量缩放是通过调整每个单元的密度,用来对每个单元调整合适的时间步。使用双精度LS-DYNA进行计算,以保证计算的稳定性。其他参数均采用默认值。
3.帆面展开过程仿真结果
•帆面展开过程分析
将五个薄膜折叠结构有限元模型展开过程的应力变化云图列于表4-23中。由于模型2与3有限元模型相同,仅施加的速度载荷不同,展开过程应力图接近,因此在表中仅列出模型2的展开过程图。
表4-23 展开过程应力状态图

续表

从表中可以看出,在薄膜四个角施加载荷时,几种折叠方式的帆面薄膜都能沿两个相互垂直的方向同时展开。薄膜采用叶内折叠方式展开时,是从靠近薄膜中心的位置由内而外逐步展平,最后展开的是薄膜最外层折叠的部分。叶外折叠和斜叶外折叠则是规则的向外展开,并且斜叶外折叠的展开过程比叶外折叠模型的展开过程更加有序。
从几个模型的展开过程图中发现了其共同点,即帆面完全展开时,每个模型施加载荷的四个顶点处都出现了应力集中现象。
•帆面展开稳定性分析
有限元建模时帆面四个顶点的Z方向坐标设为零,而帆面中心点坐标由各模型确定,因此几种模型在初始状态时中心点的Z坐标值都不相同,五个模型中心点Z方向坐标变化曲线绘于图4-66中。
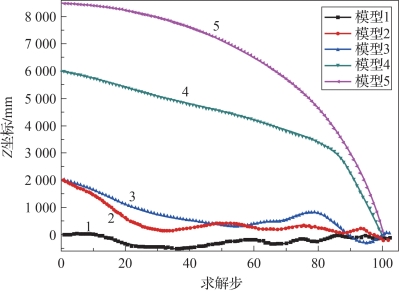
图4-66 模型Z坐标变化曲线(书后附彩插)
由图中能看出模型1到模型3这三个叶内折叠的模型,薄膜中心都出现了上下抖动的情况,结合表4-23中叶内折叠展开过程的图片,发现叶内折叠这种折叠方式在展开过程中会出现帆面的上下抖动,且抖动幅度大小与折叠宽度有关,折叠宽度越大,帆面的抖动幅度越大;而叶外折叠和斜叶外折叠这两种折叠方式在展开的过程中不会引起帆面的上下抖动情况。
•帆面展开应力分析(https://www.daowen.com)
从薄膜展开的应力图中可以看出,某些位置会出现应力集中现象,这些点需要给予关注;在薄膜各折痕交汇处的点应力情况复杂,也需要特别关注,因此选择这些点绘制其在展开过程中应力变化曲线。对不同折叠参数的五个有限元模型,选取相应位置的点。模型1选取的点的位置列于图4-67中。点P1、P2、P3都位于几条折痕的交汇处,点P4则是薄膜的顶点,也是对薄膜施加作用力的点。
在ANSYS中提取有限元每个求解步中P1、P2、P3和P4点的应力值,绘于一张图中。同时提取整个模型在计算过程中出现的最大应力值,该值有可能位于帆面的不同位置,随时间而变化。将图4-67所示模型1中四个点的应力曲线和模型整体的最大应力曲线绘于图4-68中进行比较。
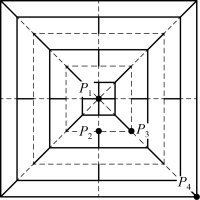
图4-67 模型1选取点位置及标号
图4-68中方块标记的曲线是整个折叠结构的最大应力曲线。从图中可以看出位于帆面中间的P1、P2、P3点应力远小于位于帆面顶点处P4点的应力,而顶点处P4点应力曲线是最接近最大应力的曲线,即帆面的顶点是帆面薄膜应力最大区域。
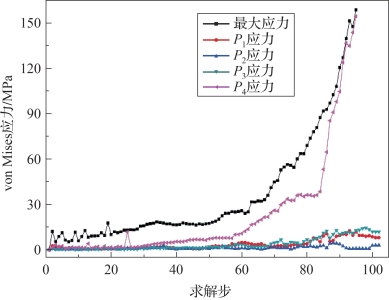
图4-68 模型1应力曲线(书后附彩插)
与图4-67中模型1选取点的位置对应,模型2选取的点的位置如图4-69所示,模型2中P1、P2、P3、P4点应力曲线和模型最大应力曲线绘于图4-70中,图中可得到与模型1应力曲线相同的规律,帆面顶点P4处应力最接近最大应力曲线。
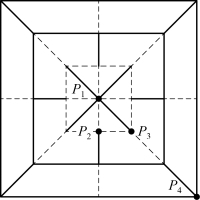
图4-69 模型2选取点位置及标号
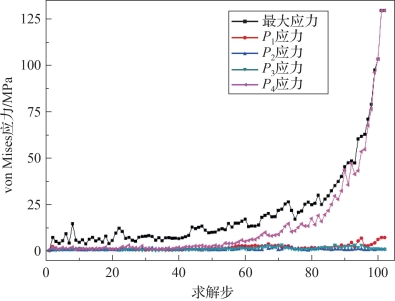
图4-70 模型2应力曲线(书后附彩插)
模型3与模型2的有限元模型相同,因此选取点的位置相同。通过建模有限元计算得到模型3的应力曲线绘于图4-71中。图中看出虽然模型3与模型2的有限元模型相同,但由于施加速度载荷大小的不同,导致帆面展开时的最大应力也不同,模型3最大应力大于模型2。
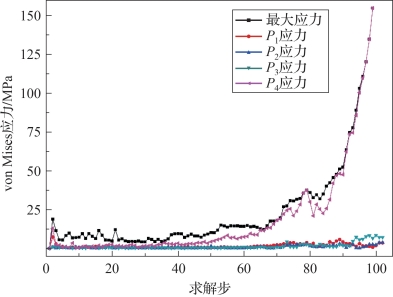
图4-71 模型3应力曲线(书后附彩插)
模型4叶外折叠方式和模型5斜叶外折叠方式与以上模型相应的选取点的位置标示于图4-72和图4-74中,相应的应力曲线绘于图4-73和图4-75中。
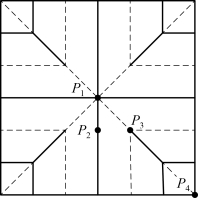
图4-72 模型4选取点位置及标号
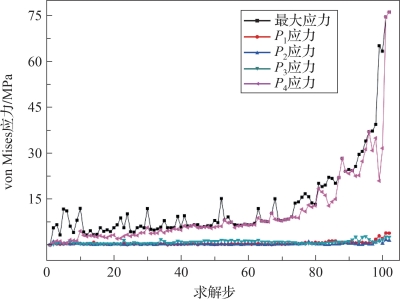
图4-73 模型4应力曲线(书后附彩插)
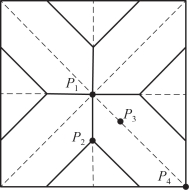
图4-74 模型5选取点位置及标号
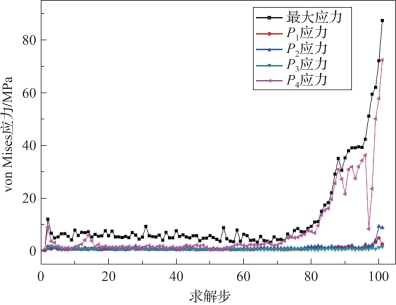
图4-75 模型5应力曲线(书后附彩插)
从应力角度,对上述结果进行总结分析:
(1)折叠宽度越小,折叠层数越多,展开时顶点的应力越大。比较模型1与模型2,将两个模型最大应力曲线绘制于图4-76中,两个模型应力相差最大时模型1的应力甚至达到模型2薄膜应力的3倍。
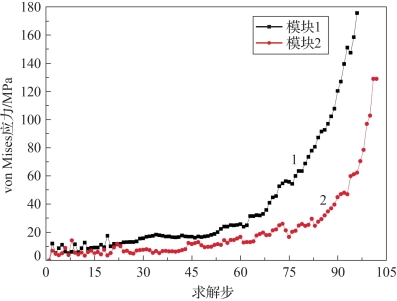
图4-76 两种折叠宽度模型最大应力曲线(书后附彩插)
(2)节点施加速度载荷越大,薄膜的应力也就越大。模型2和模型3折叠宽度都为2 m的叶内折叠,但模型2节点速度载荷是模型3的一半,将两个模型最大应力曲线绘制于图4-77中,两模型比较,应力数值差距最大时模型3的应力是模型2的两倍左右。
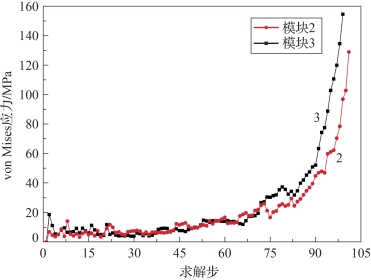
图4-77 两种速度载荷模型最大应力曲线(书后附彩插)
(3)五个有限元模型最大应力曲线对比,如图4-78所示,得出模型1(叶内折叠、折叠宽度1 m、节点速度载荷1.2 m/s的薄膜折叠模型)顶点处的应力最大,模型4(叶外折叠、折叠宽度2 m、节点速度载荷2.4 m/s的薄膜折叠模型)和模型5(斜叶外折叠、折叠宽度2 m、节点速度载荷2.4 m/s的薄膜折叠模型)两个折叠方式有限元模型在薄膜展开过程中顶点处的应力最小。
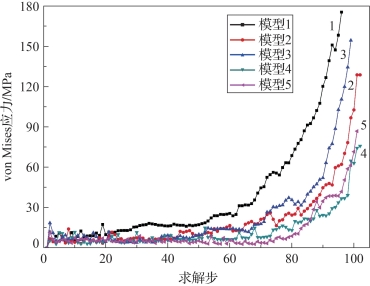
图4-78 最大应力曲线(书后附彩插)
•帆面展开率分析
薄膜材料的屈服极限为69 MPa,当帆面应力超过该数值时,帆面将会发生塑性变形,有可能会影响帆面上安装的某些仪器的精度,因此选择此数值进行帆面展开率的分析。但此数值仅作为一个参考值,用来对几种折叠方式进行比较,并非实际应用中对帆面施加的预应力的数值。
定义薄膜达到屈服极限应力时顶点位移除以理论计算中薄膜完全展平时顶点位移,得到的值为帆面展开率,用x表示。
由五个模型的最大应力曲线(图4-78)可得知模型最大应力达到69 MPa的时间t,已知该模型加载速度载荷为v,则达到69 MPa时顶点位移S1计算方法如下:
![]()
模型完全展开时理论上顶点位移为S0,则可计算帆面展开率如下:

利用上式进行计算,并将已知的速度载荷、达屈服极限时间和理论展开位移数值均列于表4-24中,得到五个模型中帆面展开率的值也列于表4-24中。
表4-24 帆面展开率
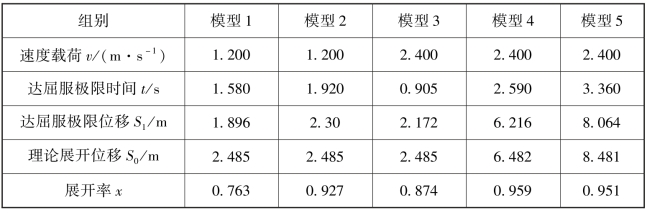
表中的数据的结果与五个模型应力曲线比较的结果是一致的:有限元模型1,即折叠宽度为1 m、速度载荷为1.2 m·s-1的叶内折叠方式帆面薄膜展开率最小,也即帆面最不平整;而模型4叶外折叠和模型5斜叶外折叠帆面,虽然施加的速度载荷是模型1的两倍,达到2.4 m·s-1,但二者的展开率都达到了95%以上,是帆面展开率相对较高的两种折叠方式。
•仿真结果分析
通过建立的五个有限元模型的计算结果,得到两方面的结论。
首先,在折叠帆面薄膜面积、施加速度载荷和折叠宽度三个参数都相同的前提下,对三种折叠方式太阳帆的展开过程进行仿真分析,比较计算结果,可得到以下结论:
(1)在帆面薄膜的四个顶点处同时施加沿对角线方向的力时,三种折叠方式都能够沿着两个相互垂直的方向同时展开,但斜叶外折叠方式展开过程更加有序。
(2)太阳帆展开时帆面的抖动情况与折叠方式有关,仅叶内折叠方式会导致帆面的上下抖动,且帆面抖动与折叠宽度有关,折叠宽度越大,帆面抖动的幅度也越大,为避免帆面的抖动,尽量不采用叶内折叠方式。
(3)由于帆面折叠产生折痕,导致帆面不可能完全展平,在帆面应力达到材料的屈服极限时,采用叶外折叠和斜叶外折叠方式的帆面展开程度最大,都达到了95%以上。
综合考虑以上各个方面,得出斜叶外折叠方式是深空太阳帆应用中较理想的帆面折叠方式。
其次,根据仿真计算时不同参数模型的比较结果,对太阳帆帆面折叠方式及展开过程提出以下几点建议:
(1)太阳帆展开时,与支撑臂相连接的帆面顶点处是整个帆面的最大应力处,应力远大于帆面其他区域,因此最好对帆面顶点处进行加固,防止应力过大导致帆面顶点区域的变形和撕裂。
(2)折叠宽度越小,折叠层数越多,帆面展开时的应力就越大,折叠宽度减小一半,应力数值差距最大时,帆面应力是折叠宽度较大时帆面应力的三倍,在满足收纳要求的前提下,选择较大的折叠宽度。
(3)帆面展开时其应力大小与支撑臂伸出的速度大小有关,速度越大,薄膜的应力也就越大,支撑臂速度加快一倍,展开过程中帆面应力甚至会变为速度较小时帆面应力的两倍,在薄膜实际展开的过程中,各方面条件允许的情况下,选择支撑臂伸出的速度越小越好。
