2.2.2　太阳帆“中心刚体＋挠性附件”动力学方程

2.2.2　太阳帆“中心刚体＋挠性附件”动力学方程

较刚体太阳帆模型，在动力学耦合系数计算过程中，太阳帆具有中心刚体加上一个挠性附件形式，挠性附件振动与太阳帆姿态和轨道相互耦合。在有限元内部计算程序中，太阳帆帆面有限元单元作为附着在太阳帆中心刚体的附件来进行耦合系数计算。挠性附件的振动将对太阳帆控制频率与精度产生主要影响。

系统的动能T包括中心刚体及帆膜和附加质量的动能，Tb、Ti、Tj分别表示中心刚体、帆膜、附加质量的动能，则系统的总动能为

设太阳帆的总形变势能为V，可得系统拉格朗日函数

将其写成拉格朗日方程，形式如下：

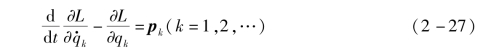
和

式中，ω＝[ωx ωy ωz ]T是太阳帆的角速度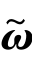，是ω的反对称矩阵。根据基本假设忽略二阶小量，经过化简整理后，可获得挠性太阳帆系统动力学方程

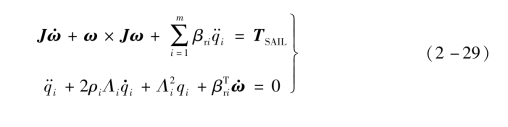
式中

J——帆膜未变形的太阳帆相对其质心的转动惯量矩阵；

ω——太阳帆相对惯性参考系的角速度；

qi——第i阶振型的模态坐标；

βri——第i阶振型的转动耦合系数；

TSAIL——作用于太阳帆上、相对于帆面未变形前系统质心的力矩；

ρi——第i阶振型模态阻尼比；

Λi——第i阶振型模态频率。

方程式（2-29）中的模态参数βri和Λi均可用有限元软件求得，模态阻尼比一般为0.005～0.01。