4.1 太阳帆构型比较与方案设计
当前已有的太阳帆结构构型形式多样，已在轨展开并进行过空间实验的太阳帆航天器均采用了正方形结构。一类是自旋展开，利用端部质量的离心力保持帆面的形状；另一类利用支撑臂展开，通过支撑臂的强度保持帆面形状。自旋展开构型的太阳帆由于其自旋特点，姿态调整难度较大，相对三轴稳定结构来说不具有优势，对于姿态调整能力本来就较弱的太阳帆而言，三轴稳定更有可能是未来发展的趋势。为了分析各种机构构型对太阳帆性能的影响，本节工作针对具有三轴稳定能力且有支撑结构的方形帆、圆形帆和叶形帆展开比较分析。对比过程中的关注点包括：帆面几何形状设计、质量惯量对比和力学分析结论等。几种构型如图4-1所示。
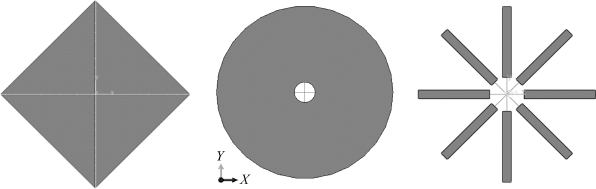
图4-1 三种太阳帆构型示意图
1.太阳帆构型设计
以等效边长160 m的方形帆面积为例，进行方形、环形、叶形三种构型的建模、仿真及讨论分析。
1）方形帆
方形帆是目前太阳帆研究中最常用的构型，其特点是加速度较高、结构稳定，力学特性比较接近传统航天器。方形160 m太阳帆航天器支撑臂长113 m，单片薄膜为接近等腰直角三角形构型，三点连接于十字型支撑臂的端点。根据前面章节的分析，方形帆可以采用RSB机构和滑块来实现三轴稳定，为了计算方形帆的大角度姿态机动，在方形帆的支撑臂上设置带质量的滑块。
2）环形帆
支撑臂为内外双环，内半径为20 m，外半径为129.57 m。薄膜为环形，内外都与支撑环相连接。内外支撑环之间可以加轻质的拉索以保证太阳帆的强度和稳定。环形帆的中心质量位于环形帆的中心，通过轻质绳索悬浮约束于内环。环形为了计算环形帆的大角度姿态机动，在环形帆的外侧支撑环上对称设置两个带质量的滑块，为了能与方形帆、叶形帆保持相同的加速度，根据比例设置质量为10 kg，在外环支撑上任意滑动。
3）叶形帆
叶形帆采用八个长条形叶片做自旋稳定以张紧薄膜帆面，叶片长度为159.54 m，宽度为20 m。叶片内侧以单根T字形连杆与中心相连接。连杆长38.24 m，T形头部宽度与叶片宽度一致，为20 m。叶形帆的大角度姿态机动与方形帆、环形帆不同。由于叶形帆需要自旋稳定，在叶片上设置质量块进行偏转控制是不够合适的，因此在中心不旋转的稳定位置设置一根长为20 m的控制杆，一端连于太阳帆中心，另一端设置质量块，控制杆和质量块合重10 kg。假设控制杆最大倾角为45°。
2.不同构型质量及惯量对比
记方形帆的对角线长为L，环形帆的直径为R，各自面积为AS与AC，两者需求梁长度分别为DS与DC，则有
假设两者面积相同，即AS＝AC，可以得到
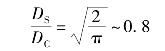
由上可知，方形帆支撑臂长度需求要少于环形帆，说明同等太阳光推力作用的方形帆比环形帆质量更小，因而具有更高的运行性能。但是，以上结论仅限于不考虑结构质量的假想模型。方形帆会在支撑臂顶端受到载荷，变形可能性较高，而环形帆则在圆周受到规整载荷。环形帆可以通过回转来减小边缘张力。具体情况，需要多方面结合进行更具体的有限元分析。
接下来初步评估方形帆和环形帆的转动惯量，太阳帆航天器机动所需的扭矩与其转动惯量成正比。考虑方形帆的单根杆长为l，并且取杆的单元长度质量为λ，忽略帆面质量而仅考虑支撑臂结构的影响，计算其对角线方向的转动惯量为
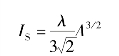
从上式中可以看到，随着太阳帆尺寸的线性递增，帆面转动惯量呈非线性递增。同样对环形帆进行分析，按照同样的单元长度质量，关于面内轴线，其转动惯量为
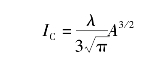
两者相比较，可以得到
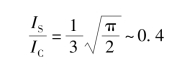
因此，在解析计算中，对于给定的面积，方形帆有更小的转动惯量，也因此具有更好的转向性能。
如果将构型扩展至正多边形太阳帆模型支撑臂，采用帆面面积与支撑臂数量之比来评价这些设计，则当杆件数目为N，杆长为R时，多边形帆的面积为
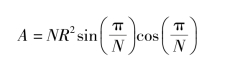
当N的数值变大，即A→πR2而
的极限情况时，该帆成为一个环形太阳帆。杆件总长度D和数量N之间的关系可以简单描述为
D＝NR
借助该结果可以得到一般性的结构利用率表达式，即
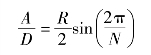
从上式中显然可以得到，当N取4时，杆件材料达到最大的利用率，太阳帆的理想几何模型是方形。
3.太阳帆预应力校验
太阳帆航天器运行过程中，由帆面自旋或支撑臂对薄膜帆面进行张紧。为了确保后续分析的正确性，本节首先需要对预应力情况进行校验分析，分别列出方形帆、环形帆、叶形帆的预应力仿真计算结果。
•方形帆预应力校验
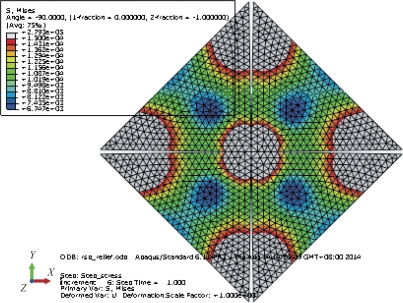
经过仿真，测得方形帆预应力最小为6 746.82 Pa，最大为279 341 Pa，预应力最小的部位在三角形帆面中心，三角形的端点为应力最大位置，如图4-2所示。
图4-2 方形帆预应力仿真结果（书后附彩插）
•环形帆预应力校验
经过仿真，环形太阳帆预应力最小为14 761.7 Pa，最大为154 098 Pa。整个帆面应力分布均匀，无特殊集中应力，如图4-3所示。
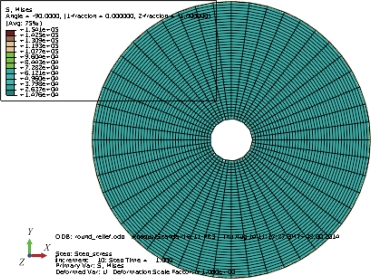
图4-3 环形帆预应力仿真结果（书后附彩插）
•叶形帆预应力校验
经过仿真，测得叶形帆预应力最小为26 639.5 Pa，最大为1.732×107 Pa，如图4-4所示。可以看到，由于帆面靠自旋张紧，帆面内外侧应力分布差距较大。内侧应力集中要高于方形帆和环形帆一个量级。
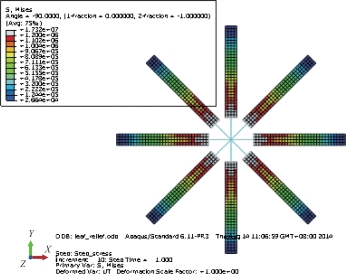
图4-4 叶形帆预应力仿真结果（书后附彩插）
4.太阳帆静力学分析
在预应力分析步计算结果的基础上，进行静力学分析。由于太阳帆航天器在轨道运行无约束，因此设置惯性释放载荷，可以计算得到太阳帆在宇宙空间的真实变形状况。
•方形帆光压变形静力学结果
经过仿真，薄膜最大变形为0.518 m，如图4-5所示。最大变形位于薄膜帆面的四个外边缘，其与帆面中心点的位移差值即为太阳帆的最大面外法向变形。
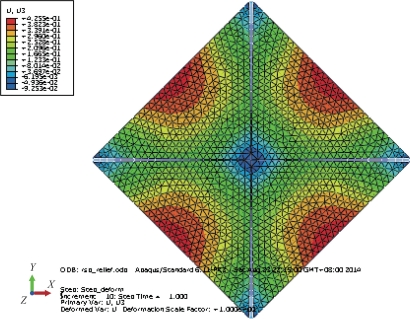
图4-5 方形帆光压静变形仿真结果（书后附彩插）
•环形帆光压变形静力学结果
经过仿真，环形帆内外缘最大法向位移偏差为0.372 9 m，如图4-6所示。由于环形帆的结构一体化特性，整个帆面的静变形非常平滑。
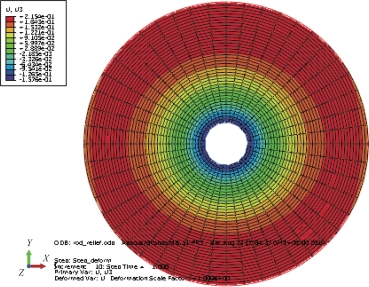
图4-6 环形帆光压静变形仿真结果（书后附彩插）
•叶形帆光压变形静力学结果
经过仿真，外缘最大变形为0.085 51 m，如图4-7所示。由于自旋稳定的效果，越靠近太阳帆中心变形越小，叶片边缘变形最大。
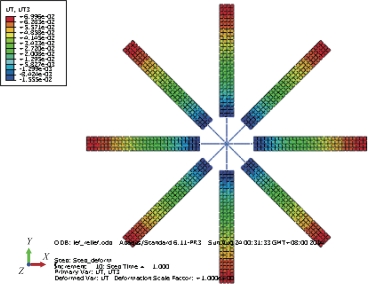
图4-7 叶形帆光压静变形仿真结果（书后附彩插）
可以看到，方形帆的变形要略大于环形帆和叶形帆，这符合构型设计的预想。方形帆的优势在于稳定性、可控性等方面，而对于100～200 m量级尺寸的太阳帆而言，0.518 m的变形在可接受范围之内。
5.太阳帆动力学分析
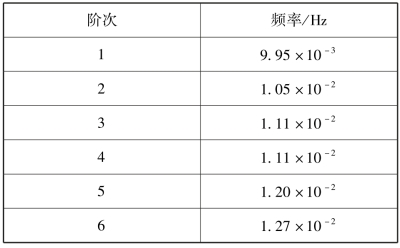
方形帆模态频率动力学结果如表4-1所示，各个阶次的频率整体相距较近，处于10-2量级，整体分布较为平均和稳定。
表4-1 方形帆频率提取结果
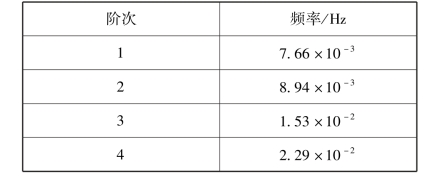
环形帆模态频率动力学结果如表4-2所示，由于环形帆构型的一体化程度较高，因此频率数值大小随着阶次的提高较快，即相近的多阶频率比较少。
表4-2 环形帆频率提取结果
叶形帆模态频率动力学结果如表4-3所示，由于叶形帆有八个帆面，因此模态较为密集，在非常相近的频率下，不同帆面上对应有相同频率的不同阶模态。
表4-3 叶形帆频率提取结果
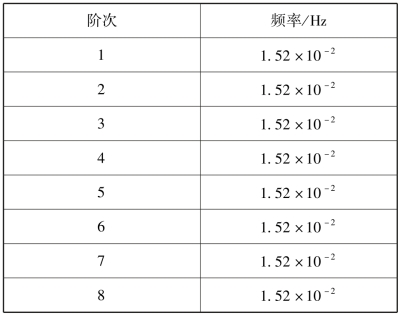
环形帆由于其整体化的结构特性，具有较好的频率特性。方形帆频率量级与环形帆相当。而叶形帆由于具有较多的叶片，整体具有较多的局部模态，从稳定性和机动控制角度而言，要略逊于前二者。但方形帆在结构简单性、操控方便性等方面具有优势，同时对于支撑结构的需求也较少，变形和质量特性的变化较小，是较为合适的选择之一。