2.2.3 太阳帆动力学耦合系数计算
根据柔性航天器中心刚体加挠性附件耦合系数计算理论模型,将太阳帆整体结构作为挠性附件,将装载太阳帆的飞行器作为中心刚体。应用有限元方法可以得出模型的耦合系数矩阵,先对两种模型分别进行结构模态分析,为耦合系数矩阵计算提供基础数据。
首先,结合中心刚体加柔性附件类航天器柔性附件对中心刚体的动力学耦合系数计算理论,得出应用有限元方法计算各耦合系数公式如下:
![]()
![]()
![]()
![]()
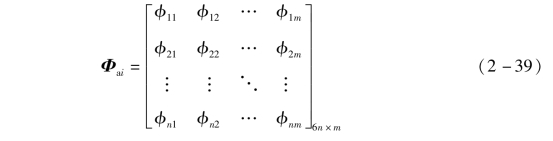
式中,Ttai,Tsai,Tai分别为对应的转换阵;Dai为附件i的刚体模态阵;mai为附件i的质量阵;Φai为附件i的正则模态阵;mrai为附件i的刚体模态质量阵。其表达式分别为
![]()
![]()
![]()
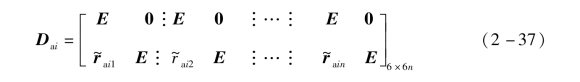

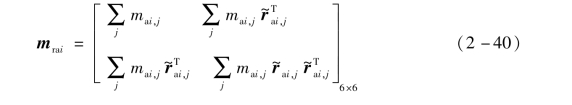 (https://www.daowen.com)
(https://www.daowen.com)
其次,对整体太阳帆有限元模型进行有限元动力学分析后,在结果文件中提取相应耦合系数计算所需矩阵。利用有限元求得前六阶模态以后,在Nastran前处理文件中加入DMAP语句,就可以在结果文件“.f06”中读取振型矩阵Φai、刚体模态质量阵mrai、附件i的质量阵mai,在前处理文件“.bdf”中读取各有限元矢量rai,j,从而求得附件i的刚体模态阵Dai。
打开“.bdf”文件,在“SOL 103”之后插入如下的dmap语句:

即可输出质量阵和刚度阵。
在Patran软件进行分析时,在“Case Control Section”卡片中加入“meffmass(all)=yes”语句,就可以输出刚体模态质量阵。插在SOL 103之后,使用Fortran语言编写计算程序,进行矩阵运算。
如图2-12所示为耦合系数计算流程图。
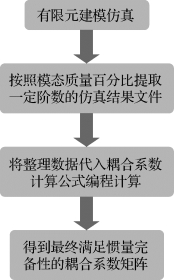
图2-12 耦合系数计算流程图
根据柔性航天器中心刚体加挠性附件耦合系数计算理论模型,将太阳帆整体结构作为挠性附件,对太阳帆整体结构进行有限元建模,从而计算其耦合系数矩阵。在对有限元模型仿真结束后,对仿真结果进行添加DMAP语句处理,按照模态质量百分比提取前n阶模态结果,得出耦合系数计算所需相关矩阵,代入耦合系数计算公式编程计算,得出相应的耦合系数矩阵。太阳帆有限元建模描述:对于太阳帆伸展臂结构,考虑其同时承受轴向拉压载荷与横向弯曲载荷,所以采用梁单元;对于帆面结构,采用膜单元模拟;对于帆面与伸展臂联结点,采用RBE2单元进行模拟;由于伸展臂、帆面作为挠性体对于结构模态特性起到决定性作用,所以将模型中心节点看作固定不动结构,将其6个自由度完全约束;帆面应力达到1个Psi时被拉紧,所以在帆面角点施加集中力,以使帆面应力满足拉紧条件。对太阳帆有限元模型进行带有预应力的非线性模态仿真,并根据模态质量比提取前8阶模态,本处仅展示第2阶、第3阶模态结果,如图2-13、图2-14所示。
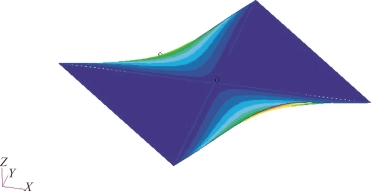
图2-13 第2阶振型(书后附彩插)
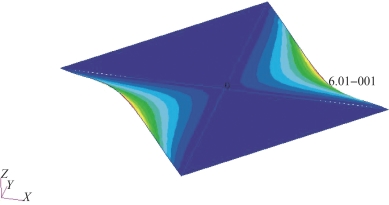
图2-14 第3阶振型(书后附彩插)
