3.2 多颗主带小行星目标选择优化方法
选取探测目标序列,从任务层面而言属于顶层任务设计阶段,这里称之为顶层设计;而当任务目标确定后,利用最优控制理论进行最终任务轨道的设计并优化性能指标,这里称之为详细优化。
同时进行多颗目标的探测,能够在节省经费的同时获得更大的科学和技术回报,多任务目标的小行星探测任务越来越被世界各航天大国强调。然而如何选取合适的探测目标和确定目标序列的探测顺序,无论是小推力还是太阳帆,对于这种连续推进的方式,目前都是一个难点和关注的热点,国际上尚无成熟通用的方法,基本处于探索阶段。对于像电推进小推力和太阳帆这种连续推力的轨迹优化和设计问题而言,需要巨大的计算量,是解析可描述的开普勒轨道的计算量无法比拟的。因而近年来,很多机构和学者对小推力的多目标探测进行了不少研究,提出了一些粗略的优化方法。目前已有的各种顶层设计方法,只能说是一种粗略的、初步的优化方法,其目的只是在满足任务指标近似最优的前提下,初步确定各个阶段的大致时间节点。这种粗略的顶层设计必须保证能对连续推进的轨道进行近似,并且不影响任务轨道的总体走向和性能指标,然而要实现这一点一般是比较困难的。
目前对于电推进小推力轨道优化的研究比较多,各研究者提出的比较常用的粗略近似方法主要包括:①圆锥曲线拼接法;②标称曲线轨道法。
对于电推进等小推力方式而言,上述两种粗略优化方法仍然存在一定局限性。同时由于多目标探测的对象一般为小行星,而小行星运行轨道规律性不强,并不像大天体那样比较接近黄道平面,如图3-1所示,列出了目前已探测到的小行星轨道半长轴与轨道倾角的关系图。
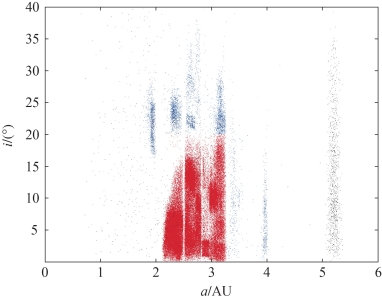
图3-1 已发现的小行星半长轴与倾角的关系统计(书后附彩插)
对于太阳帆而言,又不同于电推进等连续小推力方式。首先,太阳帆的受力特性决定了连续小推力与太阳帆的不同。太阳帆是典型的姿态轨道耦合系统,其轨道推力需要通过姿态的调整实现,因而太阳帆的姿态状况限制了其受力状况,太阳帆的受力方向只能包含半个空间,并不能实现全空间各方向的覆盖,并且太阳帆的光压力大小不仅受到太阳帆的日心距离的影响,最大受力与日心距离平方成反比,而且还与太阳帆的对日定向有关,因而即使是在半个空间可以施加推力,其推力大小并不是一个标准半球,其解空间的形状是一个半径随位置变化的椭球,因而太阳帆的推力空间是电推进连续小推力的子集,小推力的结果并不能直接拿来被太阳帆利用。以圆轨道为例,受太阳帆对日定向的姿态限制,太阳帆在切向的推力为0,因此基于沿切向施加推力的标称曲线轨道法于太阳帆基本没有可参考价值。可以说,小推力的施加结果太阳帆不一定能实现,而当小推力的燃料足够时太阳帆的推进结果是可以利用小推力完全复现的。而且,太阳帆无需燃料消耗,可以看作比冲无限大,这与一般传统的推进方式不同,因而关注的重点也不同。对于需要消耗燃料如电推进的推进方式,每一克燃料都是关注的重点,因此尽可能少的消耗燃料一般是轨道设计的目标;而太阳帆根本无需燃料消耗,关注的重点一般在飞行时间上,因此尽可能短的飞行时间一般是轨道设计的目标。对于太阳帆推进和传统的推进方式而言,二者的着眼点不同,优化目标不可比。即使脉冲与连续小推力的关系尚不清楚,但二者总是具有相同的比较指标,即燃料消耗;而对于太阳帆而言,无论电推进还是脉冲结果都没有可比性。可以这样说,与小推力的对应关系尚不清楚的脉冲粗略估计方法仅为“勉强可用”,则对没有可比性的太阳帆而言,脉冲粗略估计的方法基本没有参考价值。
上面的论述说明了顶层设计的困难之处,虽然电推进等连续小推力的顶层设计有一定粗略估计方法可用,但由于太阳帆的特殊性,小推力的结果并不适用于太阳帆,而太阳帆的顶层设计粗略估计方法尚未见公开文献有所涉及和讨论。
实际上,容易想到的是,最为原始、有效的顶层设计方法在计算能力可以满足的前提下即为穷举法。本任务中,要求在7年内实现探测3颗主带小行星的任务,对于给定推进性能的太阳帆而言,由于推进能力较弱,实现起来具有一定困难,因而探测目标的筛选和探测顺序的确定至为重要。由于太阳帆的顶层设计并无比较可靠的粗略估计方法,因而为了实现任务目标,直接利用太阳帆最优控制理论优化方法对可能作为探测目标的主带小行星进行序列的穷举,筛选出任务飞行时间符合要求的探测目标。由于现在已经发现的主带小行星数量多达数十万颗,如果对所有的小行星进行穷举筛选,其计算量之大是不可接受的。因此这里选择尺寸较大的2 065颗主带小行星作为备选探测目标,可选目标的半长轴和轨道倾角如图3-2所示,对这2 065颗目标小行星进行穷举筛选,从而选出符合要求的探测目标。
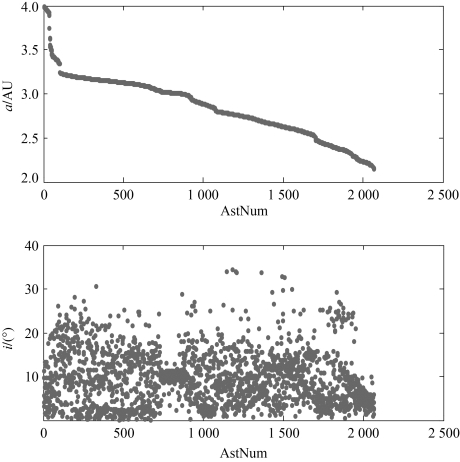
图3-2 备选的较大型小行星半长轴与倾角分布
对于多目标探测而言,如何确定探测目标以及各目标的探测顺序属于任务的顶层设计,也是影响任务成本和完成成果的关键因素。利用脉冲和电推进小推力实现多目标探测是目前研究较多的方向,而太阳帆的多目标探测研究则较少。对于双脉冲实现的方法而言,由于具有解析解,需要的计算量相对较少,一般可以利用Lambert问题求解器对可选目标数据库进行穷举计算即可得到最优结果;而电推进小推力的实现,由于也是复杂的最优控制问题,计算量比较大,难以对所有可能的探测目标进行穷举计算,所以需要一定的粗略估计方法,目前文献中用到的方法包括利用脉冲的圆锥曲线拼接法和解析曲线描述的标称曲线轨道法等,但是这些粗略方法毕竟只是对最优结果的近似,而且从一些文献研究的结果来看,近似的效果有时并不理想,因而找到更好的粗略近似方法是目前小推力多目标探测的一个难点问题。
太阳帆的推进方式决定了其受力以及任务设计的特殊性,既与脉冲方法差别巨大,又不同于小推力方法,因而上述提到的脉冲和小推力的目标序列的确定估计方法并不适用于太阳帆多目标探测。
基于目前太阳帆多目标探测并无有效的粗略估计方法,而从本任务的需求出发,为了实现7年探测3颗主带小行星,探测目标的序列确定是关键因素,时间裕度很小,可能的探测序列很难找到,因而只能利用最优控制模型,在一定的可能探测目标数据库内进行穷举计算,将任务飞行时间作为判断指标,从而直接精确地找到飞行时间满足任务要求的探测序列。(https://www.daowen.com)
而即使在2 065颗中选择3颗作为探测目标,其计算量也是巨大而不可接受的。为了进一步减少计算量,首先确定主探测目标即第三颗探测目标为灶神星(4 Vesta),如此选取的原因不仅在于灶神星是第三大的小行星,而且在于也是在2.5天文单位的柯克伍德空隙内侧最大的小行星,即相对体积大容易发现,而其位于主带内侧距离地球相对更近则飞至所需时间相对较短,选择这样的主探测目标更为合理。其次则需要利用穷举的方法确定第1号和第2号探测目标,每两个天体之间的飞行轨道按照最优控制模型进行求解,即需要对所有目标穷举从而需要大量多次求解上述最优控制问题。对于本任务,进一步减少计算量的方法是采取树状筛选方法,将整个任务分为3段,每一段设定飞行时间阈值,满足约束的目标进入下一步筛选,不满足的则筛除掉,从而减少了一部分计算量。3段全部计算完毕后,将3段飞行时间相加进行整体验证,最终将整体飞行时间满足约束条件的序列筛选出来。
最终3段的筛选阈值分别取为3年+2.5年+2年,3段的计算结果如图3-3所示。
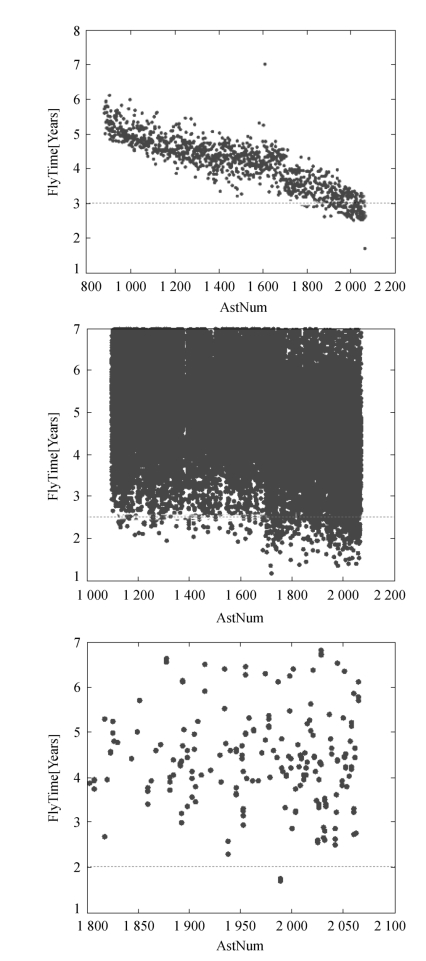
图3-3 3阶段分别筛选目标的计算结果
最后再将3颗探测目标作为整体,计算整体飞行时间进行验证,最终得到3组满足飞行时间<7年要求的序列结果,再根据飞行时间和探测目标尺寸的综合比较,最终选定一组序列作为标称轨道设计的探测目标。
影响太阳帆飞行时间的是日心转移段轨道,因此首先要确定日心转移段的轨道,进而根据日心段轨迹设计结果进一步选择地心段的发射参数。以2020年1月1日至2023年1月1日之间作为太阳帆从地球出发的可选时间窗口,利用太阳帆飞行时间最短的优化方法,在满足7年内探测至少3颗主带小行星的前提下,确定飞行时间最短的出发窗口。得出满足要求的结果共有3组,分别如下:
(1)2020年8月17日从地球出发,中途交会小行星1703 Barry和小行星1831 Nicholson,最终于2027年8月6日到达主目标小行星灶神星4 Vesta,总共飞行时间为6.97年。
(2)2021年12月30日从地球出发,中途交会小行星1089 Tama和小行星1831 Nicholson,最终于2028年12月7日到达主目标小行星灶神星4 Vesta,总共飞行时间为6.94年。
(3)2021年12月18日从地球出发,中途交会小行星1219 Britta和小行星1831Nicholson,最终于2028年9月28日到达主目标小行星灶神星4 Vesta与之交会,总共飞行时间6.78年。
3组结果中第二颗目标小行星相同,均为Nicholson,尺寸数据暂时不详,而第一颗目标小行星的尺寸分别为:1703 Barry的直径为9.41 km、1089 Tama的直径为12.92 km、1219 Britta的直径为11.43 km,可见3者尺寸相差不大。因此主要考虑飞行时间的限制,其中第3组结果飞行时间最短,最终选择第3组结果作为可行探测序列,因而首先确定了日心段从地球出发的时刻为2021年12月18日,以及出发时刻太阳帆的状态参数和初始姿态角需求,即初始α=25.02°、δ=36.90°。
则设计结果的探测序列为:地球—Britta(小行星编号1219,临时编号1932 CJ)—Nicholson(小行星编号1831,临时编号1968 HC)—Vesta(小行星编号4,即灶神星)。计算轨道时,所用的各星的参考轨道根数如表3-2所示(其中1[AU]=1.4959787066E+11[m])。
表3-2 各星参考轨道根数

