2.4.3 姿态振动耦合影响分析
本节不考虑轨道，分析姿态振动耦合效应。采用对比精确的姿态振动耦合动力学模型和近似的姿态振动半解耦模型的方法，得出姿态柔性耦合程度的强弱和相互影响量等结果。两种模型为：姿态振动耦合模型，建模时即考虑了帆膜的柔性，由姿态轨道振动耦合动力学模型直接退化得到；姿态振动半解耦模型，建模时采用的是刚体模型的姿态动力学方程，但是光压力矩项仍采用由于太阳帆柔性振动引起的。
1.主动力为光压力时姿态振动耦合分析
姿态振动耦合模型和姿态振动半解耦模型的光压力矩变化规律、姿态欧拉角和角点处横向变形规律的对比如图2-34、图2-35、图2-36所示。
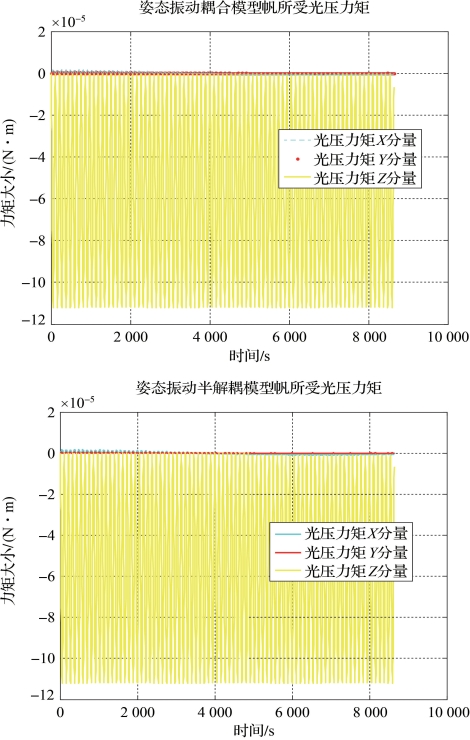
图2-34 两模型中帆所受的光压力矩对比（书后附彩插）
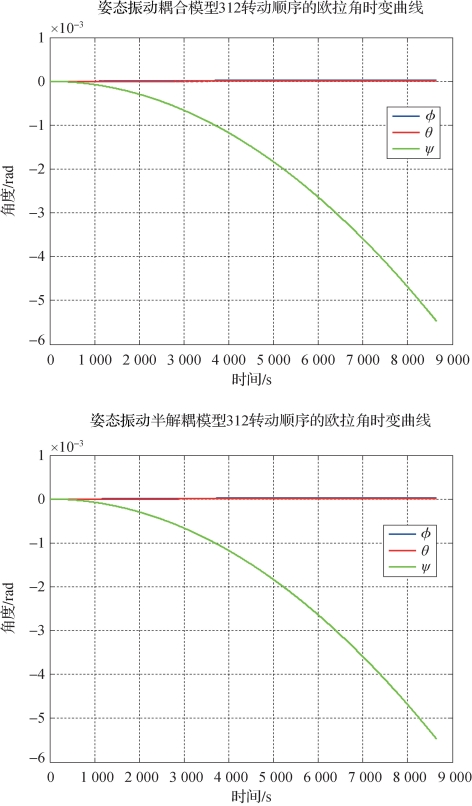
图2-35 两模型情况下太阳帆姿态欧拉角对比（书后附彩插）
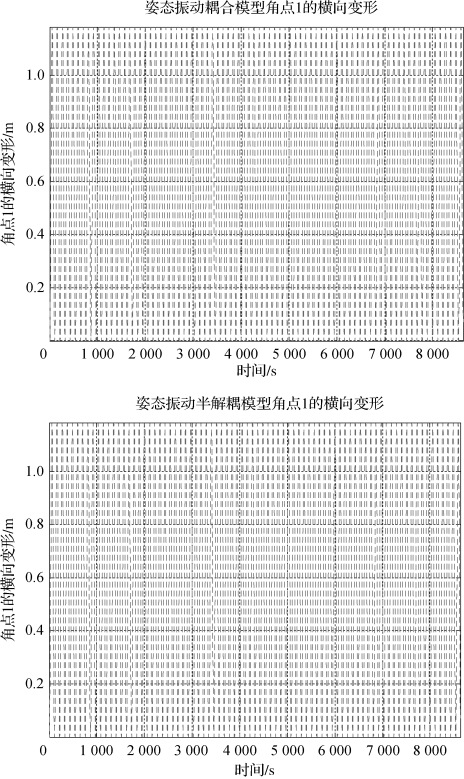
图2-36 两模型角点处横向变形对比
分析与结论：在主动力仅为光压力作用下，两种模型下太阳帆的姿态、柔性变化规律几乎相同。说明在此情况下，太阳帆姿态的变化几乎等价于是由柔性产生的光压力矩产生的，柔性振动规律几乎等价于在太阳光压力下的弹性强迫振动。这样即说明在此情况下，太阳帆姿态柔性的耦合与建模时的众多耦合系数项关系并不大，从而分析姿态柔性耦合时可以利用物理意义比较明显的姿态振动半耦合模型。
2.主动力为太阳引力时姿态振动耦合分析
姿态振动耦合模型和姿态振动解耦模型的振动回复力变化规律、角点处横向挠度变化规律、引力梯度力矩变化规律和姿态欧拉角变化规律的对比如图2-37～图2-40所示。
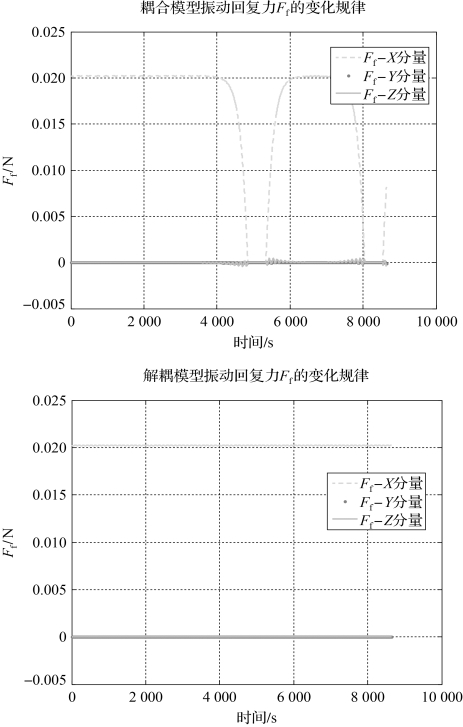
图2-37 两模型下振动回复力变化规律
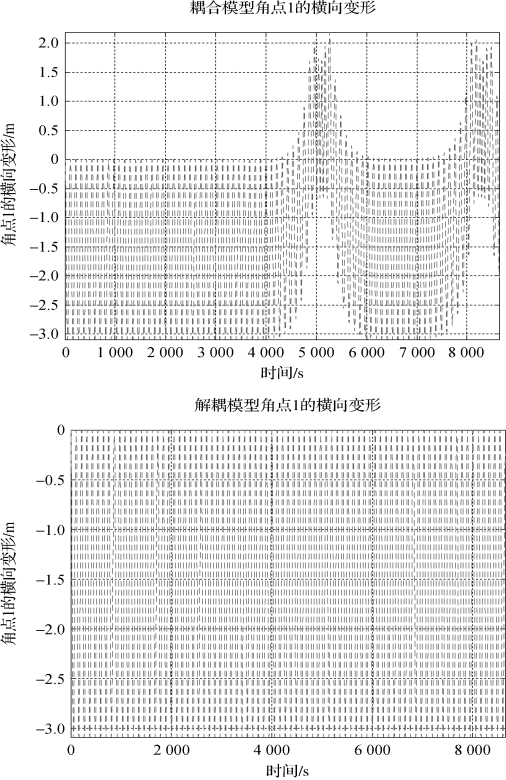
图2-38 两种模型角点处的横向挠度
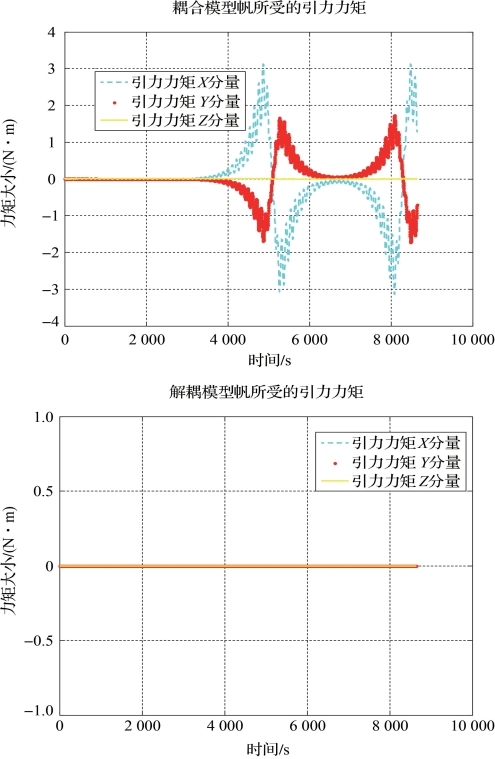
图2-39 两模型下太阳帆所受引力梯度力矩（书后附彩插）
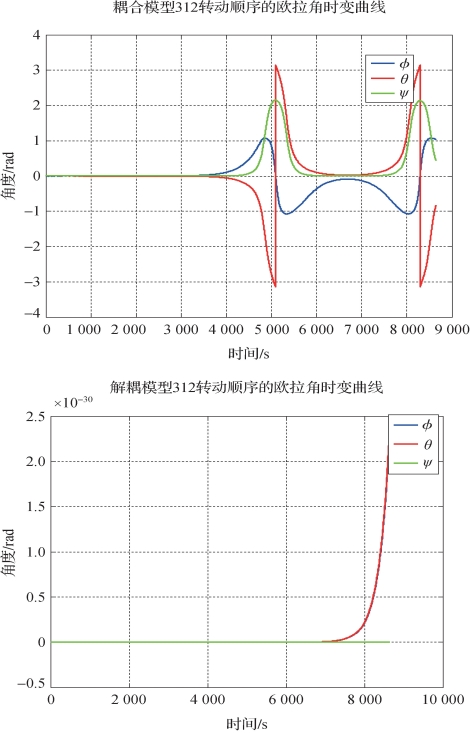
图2-40 两模型下太阳帆姿态欧拉角的变化（书后附彩插）
分析与结论：刚体模型下太阳帆所受到的引力梯度几乎为零，从而姿态角几乎为零。两种模型的仿真结果相去甚远。仿真发现，造成这种差异的主要原因是解耦模型中舍去了姿态振动耦合项
和
、耦合惯性力项，而且静距和惯性矩的计算均舍去了柔性的影响。太阳引力成为引起帆膜振动的回复力，在不考虑轨道的姿态振动耦合模型中引起的振动幅度较大，从而产生的变形比较大，从而姿态发生了较大的变化。两种模型的对比说明了考虑主天体引力时，不宜将轨道隔离出来单独研究姿态。