4.4.1 太阳帆帆面折叠技术研究
对平面薄膜,主要有以下三种基本的折叠方式:卷曲折叠、 “Z”型折叠以及“L”型折叠,如图4-44所示。 “L”型折叠也叫作单叶折叠结构,它是由1998年日本学者Kobayashi利用矢量分析法对树叶的展开过程进行了详尽的几何分析而得,如图4-45所示。
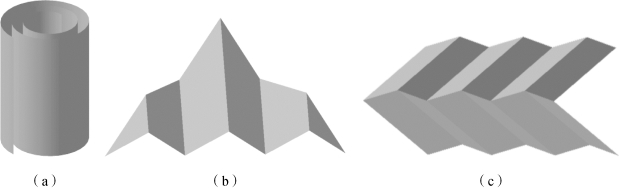
图4-44 三种基本折叠方式
(a)卷曲折叠;(b)“Z”型折叠;(c)“L”型折叠

图4-45 单叶折叠结构
在这三种折叠方式中,卷曲折叠和“Z”型折叠是对薄膜单个方向的折叠,而“L”型折叠则能够对薄膜两个方向同时折叠,提高了折叠效率。在这三种折叠方式的基础上可以衍生出各种针对不同形状平面薄膜的折叠方法,也可利用几种折叠方式的组合形式对平面薄膜进行折叠。
1.帆面折叠力学分析
太阳帆帆面需要折叠以达到最小体积,折叠过程主要可分为三个阶段:未折叠状态、折叠中状态和完全折叠状态。
折叠角定义为θ,如图4-46所示。折叠角θ=π/2时,薄膜是未折叠的状态,如图4-46(a)所示,t为薄膜厚度;折叠角0<θ<π/2时,薄膜处于折叠中的状态,如图4-46(b)所示,定义折叠的曲率半径等于折叠区域对应的曲率中心到中性面的距离,记为R;折叠角θ=0时,薄膜为完全折叠的状态,如图4-46(c)所示,通常将完全折叠时的折叠曲率半径称作折叠半径,用r表示。
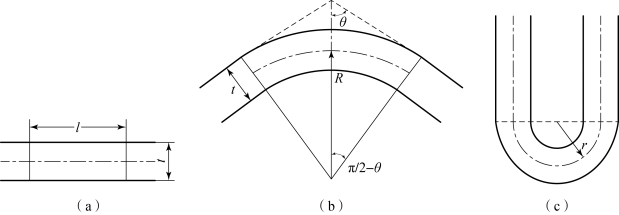
图4-46 薄膜折叠过程
薄膜厚度为t,折叠区域长度为l,中性面是图中虚线所示部分,假设中性面应变为零,则
![]()
如图4-46(b)所示,可以得到内外表面折叠后的长度分别为
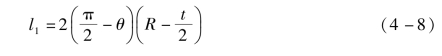
![]()
折叠时内表面受压,压缩应变为ε1;外表面受拉,拉伸应变为ε2,利用式(4-8)、式(4-9)则可以得到内表面压缩应变ε1和外表面拉伸应变ε2为
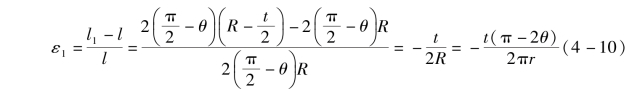
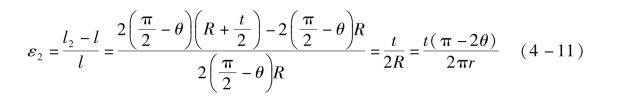
可见内表面与外表面应变的大小相同,只是伸长与缩短的区别,只表示其大小,可统一表达为

实际上,这些折痕只是微小变形,可做一理想假设:整个折叠过程中,折痕可以看作是薄膜的弹性形变,最大应力低于薄膜的屈服极限。假设薄膜的弹性模量为E,由胡克定律σ=E·ε,则内表面和外表面承受的应力大小相等,方向相反,统一表示为
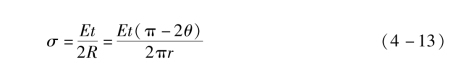
引入曲率的概念,定义曲率β等于折叠半径r与材料厚度的比值:
![]()
那么,可以得到


整个折叠过程中内表面始终受拉,外表面始终受压,且当薄膜曲率一定时,两个表面的应力随折叠角呈线性变化,折叠角越小,应力越大。也就是说,当完全折叠时应力达到最大。此时应力应变表达式为


表明折叠区域的最大应变和最大应力都只是曲率的函数,曲率越大,应力和应变越小。而增大曲率的办法有增大折叠半径和减小薄膜厚度,避免在折叠时产生较大应力。
对于8 μm厚、弹性模量为2 500 MPa、屈服强度为69 MPa的Kapton材料,绘制薄膜最大应力σ与折叠半径r的关系曲线,如图4-47所示,可知两者呈反比关系。
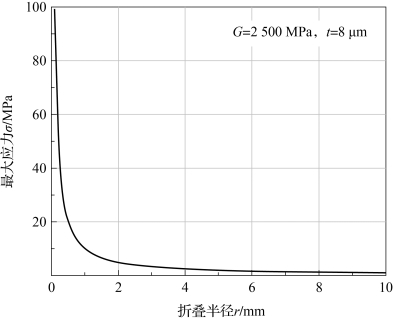
图4-47 最大应力σ与折叠半径r关系曲线
令最大应力等于材料的屈服极限,即σ=69 MPa时,利用式(4-18)计算得到折叠半径r=0.145 mm。
由上述计算发现,8 μm厚Kapton薄膜折叠半径大于0.145 mm时,薄膜完全折叠时最大应力小于其屈服极限,折叠后不会出现折痕;而折叠半径小于0.145 mm时,薄膜完全折叠时会引起折痕处薄膜材料的塑性变形,从而使得折叠后薄膜在展开时仍有折痕存在,导致薄膜展开时的不平整。
对于空间太阳帆面的折叠,需尽量减小收纳空间,并对折叠好的帆面抽真空,因而折叠半径小于0.145 mm,帆面折叠一定会产生折痕。
2.帆面折叠技术要求
对于利用支撑臂展开的大型方形太阳帆,为使帆面易于折叠存储,且帆面能顺利展开,展开方式简单可靠,对帆面折叠的要求如下:
(1)折叠方式简单,易于反复折叠;
(2)薄膜折叠后高度可调,以满足对帆面收纳时高度的要求;
(3)在方形帆面四个顶点同时施加拉力时,帆面能沿两个相互垂直的拉力方向同时展开,即帆面可以随着支撑臂伸出的同时逐步展开,展开过程一步到位;
(4)采用该种折叠可使帆面展开过程有序,防止展开时相互干扰造成帆面的缠结;
(5)折叠可能会对薄膜造成不同程度的损伤,使得薄膜材料发生塑性变形,进而产生折痕,影响材料性能,因此应该使折叠产生的折痕长度越短越好。
3.方形帆面折叠方式选择
1)方形帆面折叠方式
利用上文中介绍的卷曲折叠、 “Z”型折叠以及“L”型折叠的不同组合方式,可以得到多种适用于正方形薄膜的折叠方式。
•Miura-ori折叠方式
将单叶折叠结构(即“L”型折叠)沿着中线平行排列,可以得到Miuraori折叠结构,如图4-48所示。二维可展开结构Miura-ori折叠是于1985年由Miura和Natori共同设计的,并且成功运用到太阳电池板中。

图4-48 Miura-ori折叠
虽然Miura-ori折叠的折叠效率较高,且易于展开,但是对于大面积太阳帆则折叠困难,折叠可重复性差,因此到目前为止,Miura-ori折叠尚未应用于太阳帆面的折叠中。
•叶内折叠方式
对于方形平面薄膜,由四个单叶折叠结构的叶尖沿对角线方向汇集于中心形成的折叠结构称为叶内折叠结构(图4-49),这种折叠结构是于2002年由Guest和Defocatiis基于仿生学提出的。

图4-49 叶内折叠方式
对于方形帆面的叶内折叠方式,如果沿着两条中线将其划分为四块大小相同的正方形,则每块方形薄膜都是“L”型折叠方式,是一个单叶折叠结构,叶内折叠即由此命名;若沿着正方形的两个对角线方向将其划分为四块大小相同的等腰直角三角形,则每块三角形薄膜都是类似于横向的“Z”型折叠方式,区域划分情况如图4-50所示。
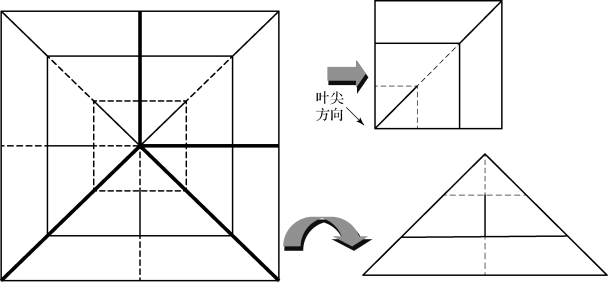
图4-50 叶内折叠区域划分
由于方形帆面积巨大,一般采用沿方形帆对角线方向,将帆面划分为四块三角形帆面,再对三角形帆面分别折叠的方式实现太阳帆面折叠。日本成功发射的IKAROS即采用叶内折叠方式进行初步折叠,每块三角形帆面采用类似于横向的“Z”型的折叠方式进行折叠,折叠完成后再将其卷在中心柱体上。(https://www.daowen.com)
但是将这种折叠方式应用于太阳帆折叠时需额外设计帆面展开辅助机构,以保证帆面展开有序性,需使用辅助机构分两步实现帆面完全展开。
•叶外折叠方式
将若干片树叶的叶柄汇集于中心,叶尖向外形成的结构称为叶外折叠结构(图4-51),这种折叠结构与叶内折叠结构由Guest和Defocatiis同时提出。

图4-51 叶外折叠方式
按不同方式对其进行区域划分(图4-52):将其划分为四块大小相同的正方形,每块方形薄膜都是“L”型折叠方式;按两条对角线方向划分,每块三角形区域都是沿竖向的“Z”型折叠方式。
相比于叶内折叠方式,叶外折叠更适合应用于帆面分块方形帆的折叠,折叠好的帆面可随着支撑臂伸展同步展开,不需要辅助机构,展开过程简洁快速。
NASA于2010年11月第二次发射的NanoSail-D2以及英国萨里大学正在研究的CubeSail均采用叶外折叠及展开方式,每块三角形帆面采用图4-52左下角所示的“Z”型折叠,帆面单独折叠完成后再将其卷到中心卷轴上,如图4-53所示。
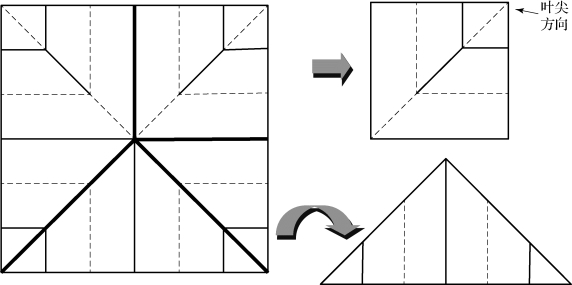
图4-52 叶外折叠区域划分
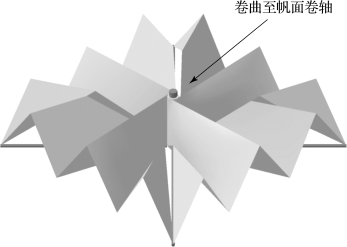
图4-53 叶外折叠应用于帆面折叠的方式
采用这种折叠方式,每块三角形帆面的斜边在最外端,在支撑臂伸出的同时带动帆面展开。帆面最先展开部分是最外端的三角形帆面斜边部分,帆面面积较大,但是展开初期所能提供的供帆面展开的空间较小,大部分帆面处于褶皱状态,如图4-53所示是理想状态下的帆面形状,在实际情况中,由于帆面很薄且柔软,会堆积在支撑臂所能提供的空间内。当太阳帆面积逐步增大时,展开初期堆积的帆面面积会更大,导致帆面展开的无序,严重时可能会造成帆面的缠结。将其应用于大面积太阳帆折叠时仍存在展开过程无序的问题,需进一步改进帆面折叠方式。
•斜叶外折叠方式
在针对方形薄膜的叶外折叠结构基础上做一改进,将四个单叶折叠结构叶尖朝外、叶脉沿方形膜中线方向汇集于中心形成新的折叠结构,称其为方形薄膜的斜叶外折叠结构,如图4-54所示。

图4-54 斜叶外折叠方式
对于斜叶外折叠方式,类似于叶内折叠结构和叶外折叠结构,同样的有如下分析,如图4-55所示:沿中线将薄膜划分为四块大小相同的正方形,每块方形薄膜都是沿对角线方向的“Z”型折叠方式;而沿两个对角线方向将其划分为四个等腰直角三角形,每块三角形区域都是“L”型折叠方式,即叶尖沿中线朝外的单叶折叠结构,这也是斜叶外折叠方式命名的由来。
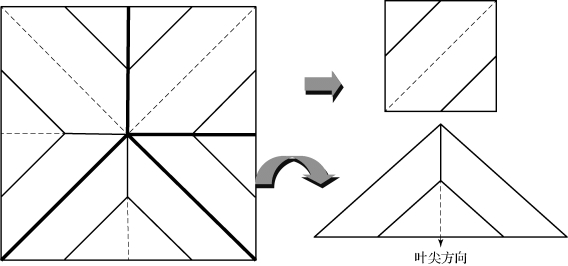
图4-55 斜叶外折叠区域划分
应用于太阳帆时,每个三角形帆面采用“L”型折叠,如图4-56所示,将折叠完成后的帆面卷在卷轴上。

图4-56 采用“L”型折叠的三角形帆面
采用这种方式折叠的太阳帆,帆面展开过程稳定有序,既有叶外折叠方式的优点,即折叠好的帆面可随着支撑臂伸展同步展开,不需要辅助机构,展开过程简洁快速,同时又改进了对大面积太阳帆叶外折叠方式展开过程无序的问题。
2)方形帆面折叠参数分析
将叶内折叠、叶外折叠和斜叶外折叠这三种折叠方式完全展开时的平面折痕示意图和折叠之后平面示意图分别列于表4-18中。
表4-18 三种折叠方式示意图
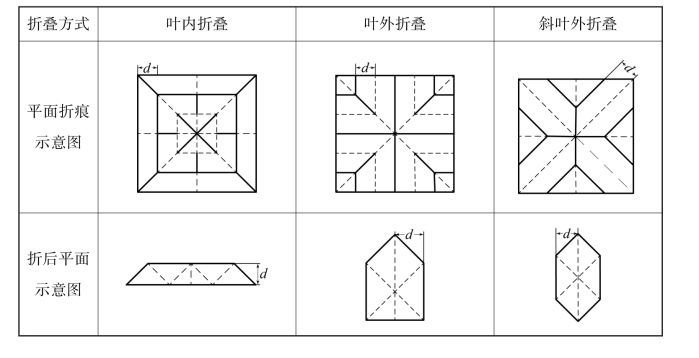
表中d代表折叠宽度,用l代表帆面边长。折叠之后薄膜的边被折痕等分为若干段,将边长被等分段数值的一半称为帆面的折叠层数,如表4-18中叶内折叠和叶外折叠的折叠层数为3层,而斜叶外折叠的折叠层数为2层。
折叠宽度相同时,叶内折叠和叶外折叠两种折叠方式的折痕长度和折叠层数都相同,分别用L1和n1表示。对于斜叶外折叠方式,折痕长度和折叠层数分别用L2和n2表示。薄膜的折叠层数由折叠宽度确定,则可以得到帆面边长、薄膜折叠层数与折叠宽度之间的关系式如下:
![]()
![]()
薄膜折叠层数只能为整数,因而对上面两个式子中比值部分取整,式(4-19)及式(4-20)中括号即代表取整,再在所取整数值上加一,得到薄膜最终折叠层数。当帆面边长确定时,折叠宽度与折叠层数呈反比关系,且折叠层数仅与折叠宽度有关。由式(4-19)和式(4-20),n1≥n2,即同等折叠宽度下,斜叶外折叠的折叠层数更少。
通过计算分析,对于叶内折叠和叶外折叠方式,折痕长度L1与折叠宽度d的关系式列于式(4-21),斜叶外折叠方式折痕长度L2与折叠宽度d的关系式列于式(4-22):


帆面边长一定时,折痕长度由折叠宽度决定,二者呈反比关系。式(4-21)和式(4-22)比较,得到L1>L2,即采用叶内折叠和叶外折叠方式薄膜的折痕长度大于采用斜叶外折叠方式薄膜的折痕长度。
令帆面边长l=12m,折叠宽度d=2m,利用式(4-19)和式(4-20)计算三种折叠方式的折叠层数,用式(4-21)和式(4-22)计算折痕长度,得到的计算结果列于表4-19中。
表4-19 三种折叠方式的折叠层数及折痕长度
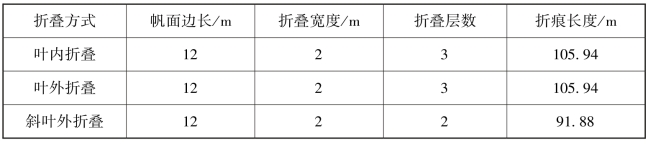
从表中可以看出对同样大小的帆面进行折叠时,在相同的折叠宽度下,斜叶外折叠的折叠层数最少,且折痕长度最短,因折叠引起材料变形区域小,对帆面材料的损伤相对较小。
结合上文所述,相比叶内折叠和叶外折叠方式,斜叶外折叠的折叠方式简单,折痕长度较短,展开过程简洁有序,帆面展开时不需要复杂的辅助机构,是更适合应用于有支撑臂的、由四块三角形帆面组成的大型方形太阳帆面的一种折叠方式。
4.帆面折叠方案
为了得到足够的推力,太阳帆航天器需要有很大的面积,大型太阳帆的帆面整体制造拼接以及帆面折叠都很困难,因此很多国家都采用帆面分块制造、分别折叠的方式。目前多数太阳帆都采用正方形的构型,沿方形帆的对角线方向,将帆面划分为四块等腰直角三角形帆面。如上文所述,斜叶外折叠方式比叶外折叠和叶内折叠更适用于大型方形太阳帆面的折叠,将其应用于帆面折叠,具体过程如下:
每个三角形帆面采用“L”型折叠方式进行初步折叠,具体折叠步骤如图4-57所示。
将三角形帆面按图4-57中所示标注,D为斜边BC的中点,将一块帆面沿AD段对折,根据对帆面折叠收纳后宽度的限制h,将AD等分为n段,在各均分节点处做两条直角边的平行线,采用图中所示方式沿着直角边的平行线往复折叠,直至最后一个节点,完成帆面的“L”型折叠。
帆面采用“L”型折叠后高度等于其折叠宽度d,折叠宽度可由下式计算:

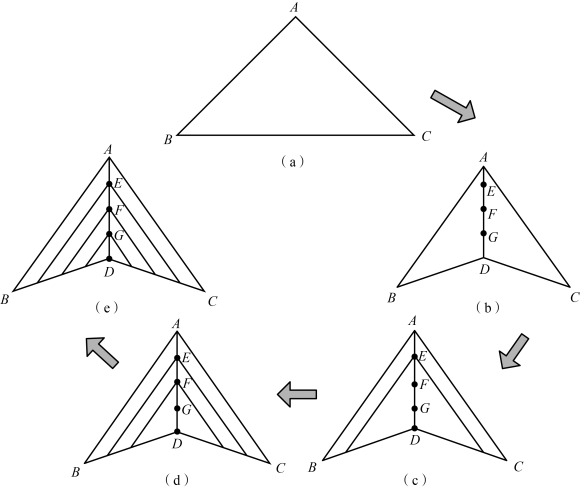
图4-57 “L”型折叠过程
由于帆面收纳后高度必须小于规定高度,即d≤h,则n取满足不等式d≤h的最大整数值。
(1)单个三角形帆面固定并卷在卷轴上,步骤如下:
折叠完成后帆面的直角顶点固定在帆面卷轴上,把折叠好的长条状帆面逐步紧凑的卷在帆面卷轴上,最终收纳完成后,三角形帆面的两个斜边顶点都留在了帆面卷轴的最外端;固定并卷曲的过程如图4-58所示。
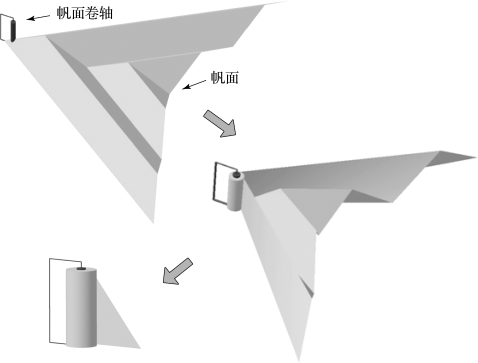
图4-58 三角形帆面固定卷曲过程
(2)将四个帆面卷轴围绕中心放置,完成相邻帆面以及帆面与支撑臂的连接,以便于在支撑臂展开的同时带动帆面展开,完成帆面整体的折叠与收纳,结合图4-59和图4-60,详细描述如下:
把四个帆面卷轴围绕中心位置对称放置,四个帆面卷轴之间留有一定间隔,防止因距离过近导致帆面展开时相互干扰,图4-59是整体收纳之后的三维立体图,图中仅简单画出支撑臂卷轴及支撑臂伸出端方向,不涉及支撑臂的展开辅助机构,用以说明帆面与支撑臂放置的相对位置及连接方式。
图4-60为图4-59中所展示的帆面整体收纳结构的俯视图,用来说明支撑臂与帆面的连接方式。由于每个帆面卷轴最外端都留有三角形帆面两个斜边顶点,当帆面卷轴和支撑臂卷轴围绕中心柱体间隔放置时,三角形帆面的两个斜边顶点分别贴近两侧的支撑臂,将支撑臂卷轴的伸出端与其两侧帆面卷轴上的与支撑臂相邻的两个斜边顶点相连,支撑臂卷轴Ⅰ分别与两侧帆面卷轴的相邻顶点1B和2A相连接,完成一个支撑臂与帆面的连接,相应地将四个支撑臂都与帆面进行此类连接,完成帆面整体的收纳。
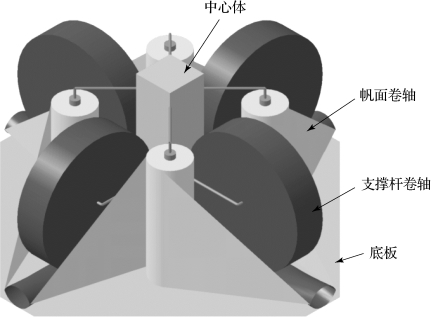
图4-59 帆面整体收纳示意图
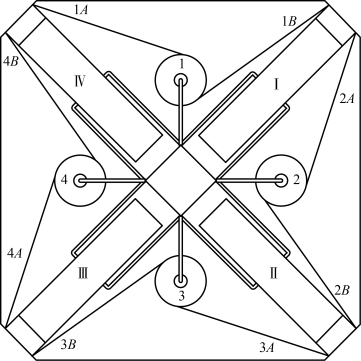
图4-60 帆面与支撑臂连接方式说明图
(3)当帆面展开时,四根支撑臂卷轴沿帆面展开时的对角线方向逐步伸展,带动帆面卷轴转动,实现帆面的逐步展开。折叠及展开方式简单,帆面展开过程有序,适用于各种类型的支撑臂,不需要复杂的展开辅助机构。帆面展开一半时的状态如图4-61所示。

图4-61 帆面部分展开状态示意图
