2.2.6 太阳帆全柔性动力学方程
定义太阳帆系统质心O在惯性坐标系OIXIYIZI中的位置矢量为c，任取太阳帆系统上一个质量微元mk（k＝0，1，…，n），相对于质心O的位置矢量为rk，其柔性变形位移为ρk，则该质量微元mk在本体系中的位置矢量为
在惯性系中的位置矢量为
矢量间相互关系如图2-23所示。
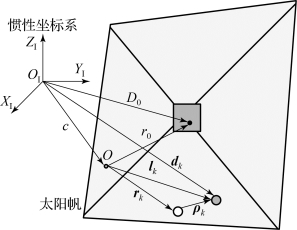
图2-23 质量微元矢量定义
由于rk表示质量微元mk结构上的位置关系，是固定矢量，所以其导数为0。
在惯性系中质量微元位置矢量dk的一阶和二阶导数为
其中，定义叉乘关系式
表示矢量u的叉乘矩阵，为斜对称矩阵。
定义模态位移为η，由质量微元模态位移坐标转到实际物理振动位移的转换矩阵为Φ，该阵的大小为3n×m，其中n是太阳帆上质量微元数目，m是模态数目。相互关系可以用以下数学表达式：
质量微元mk的线动量为
太阳帆系统的线动量为
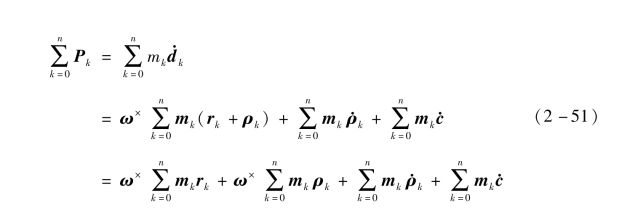
由于O是太阳帆系统的质心，所以
代入模态位移关系式（2-49），并且省略二阶小量mk ρk，根据牛顿第二定律，可以得到太阳帆系统运动的线动量方程：
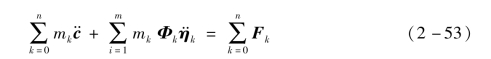
令mT＝∑mk为太阳帆系统的总质量；FT＝∑Fk为太阳帆系统的总外力；Btran为
前的系数矩阵，得到
质量微元mk对质心O的角动量是
整个太阳帆系统的角动量为
式中，I是太阳帆航天器卫星平台部分的转动惯量，由于安装等误差，该阵为非对角阵。
对整个太阳帆系统的角动量公式（2-56），求导得到力矩方程：
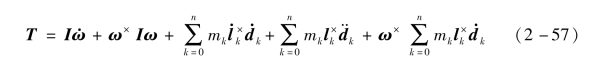
式中，T是作用在整个太阳帆系统上的外力矩。
认为太阳帆角速度为ω小量，省略二阶小量项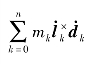
和
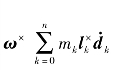，得到
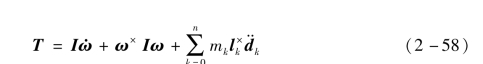
下面推导在所有内力作用下整个太阳帆系统的质心和每个质量微元mk的惯性运动学方程：
省略包含mω的二阶小量项，并根据如下关系式：
得到
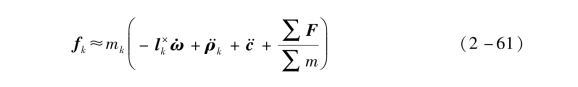
式中，fk是作用在质量微元mk上及其附近的总内力。总内力也可以用相互之间弹力的形式表达，即
式中，kkj是结构的物理特性，Fk是外力。结合内力定义式（2-61）得到
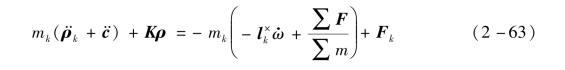
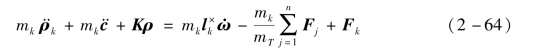
式中，矩阵K是对称且满秩的，对于三维空间的位移，ρ规模是3n×1，K是3n×3n。下面用N代替F前面的系数矩阵，可以得到矩阵形式的柔性太阳帆振动方程：
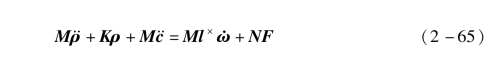
式中，F是作用在太阳帆上每个质量微元外力矩阵。
振型矩阵Φ满足正交定理：
式中，M是质量阵，E是单位阵，Ω2是对角阵。矩阵形式模态坐标方程可以变换为
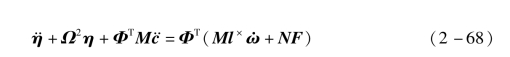
给出考虑结构阻尼的柔性系统模态坐标动力学方程：
式中，Z是模态阻尼矩阵，u是在质量微元上的控制输入。
将质量微元位置矢量二阶导数
的表达式（2-46）代入力矩方程式（2-57），省略含有
和
的非线性项，得到
下面推导太阳帆系统整体的转动惯量IT。如图2-24所示，在坐标系OXYZ中取质量微元mi，其位置矢量为ri，距离任意轴距离为di，图中e为任意轴的单位矢量，则对过O点任意轴e的转动惯量为
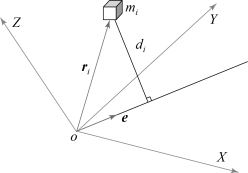
图2-24 任意轴的转动惯量
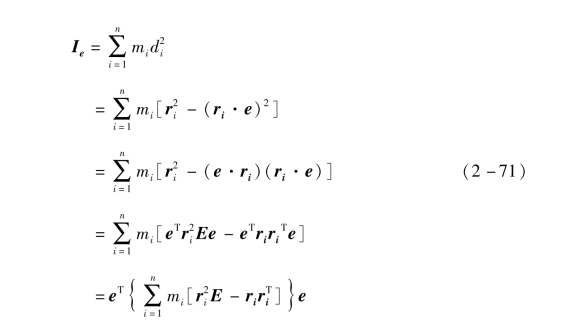
可以证明，式（2-71）中子因式满足如下关系：
太阳帆中心刚体的转动惯量为I，代入式（2-71）和式（2-72），故其带上柔性帆的整体系统转动惯量为
将力矩公式（2-70）代入关系式（2-60）和如下三个关系式：
和式（2-49）得到如下模态坐标形式的力矩关系式：
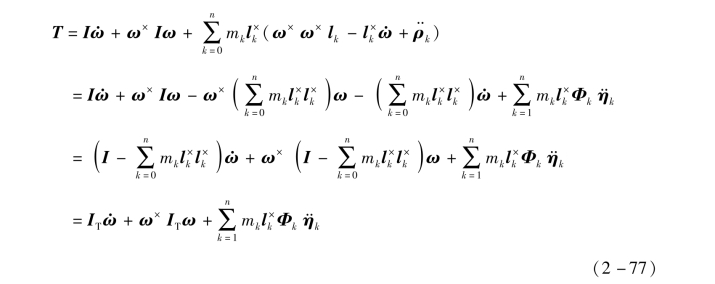
令式（2-77）中
前的系数矩阵为Brot，由下面两个关系式：
得到
根据式（2-77）可以得到整体太阳帆的姿态动力学方程，根据式（2-68）、式（2-69）和式（2-80）可以得到整体太阳帆的柔性振动方程，联立二者得到
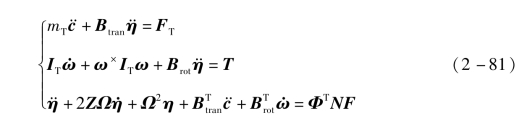
下面比较柔性太阳帆姿态动力学与带挠性附件卫星姿态动力学方程的区别之处。带挠性附件卫星姿态动力学是基于中心刚体加挠性附件形式建模的，其经典带挠性附件卫星动力学方程在屠善澄和李宝绶的著作中给出：
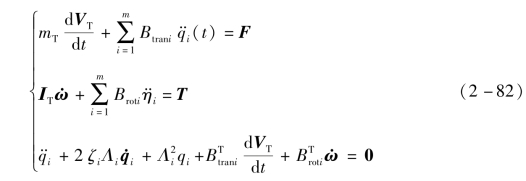
动力学方程组（2-81）和方程组（2-82）虽然形式上大致一样，但有着本质区别：
首先，带挠性附件卫星姿态运动方程中转动惯量是未变形时卫星的转动惯量，而柔性太阳帆姿态运动学方程中的转动惯量为时变转动惯量。
其次，柔性太阳帆姿态动力学模型中模态坐标方程右端给出了广义力的具体形式，而卫星姿态动力学模型中挠性附件不受外力和外力矩。
最后，柔性太阳帆姿态动力学模型中模态坐标表示每个质量微元的模态位移，可以转换为太阳帆上每一点的物理位移，而带挠性附件卫星挠性附件运动方程模态坐标表示每个挠性附件的模态位移。
如果仅仅是套用带挠性附件卫星的常规结果，得出来的动力学方程无法完全反映太阳帆构型的连接关系。