3.4.4 太阳帆动力学模型对控制结果的影响分析
以质量为200 kg太阳帆航天器为例。针对刚体太阳帆模型、全帆形式太阳帆非线性姿态动力学模型和全杆形式太阳帆非线性姿态动力学模型，以及全柔性太阳帆动力学模型，采用太阳帆非线性PID姿态控制器分别进行数值仿真分析。
设太阳帆初始姿态角为：ϕ（0）＝-80°，θ（0）＝10°，ψ（0）＝10°，轨道半径为1 AU。在短期响应测试中，使用斜坡信号（2°／h）作为参考输入分别对3个轴的姿态控制系统进行测试。
在3个轴上设
，即3个轴的初始角速度均为零。并认为模态坐标初始位置为零，模态坐标初始导数为零，这样可以避免初始模态坐标对姿态产生干扰，直接观察姿态激起模态振动的影响。
对挠性太阳帆进行有限元建模，将全帆分成489个单元，并观察4个尖端点和帆面边缘的中点随着姿态控制而变形的情况，相关点的编号如图3-38所示。
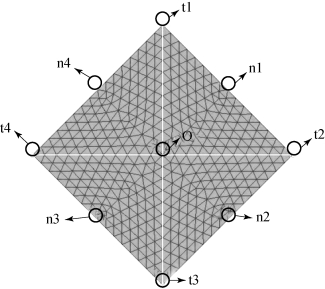
图3-38 太阳帆尖端点和帆中点
1.刚性太阳帆模型的姿态稳定和姿态机动控制
首先研究刚性太阳帆的姿态稳定控制。仿真时间为4 h，仿真结果如图3-39所示。
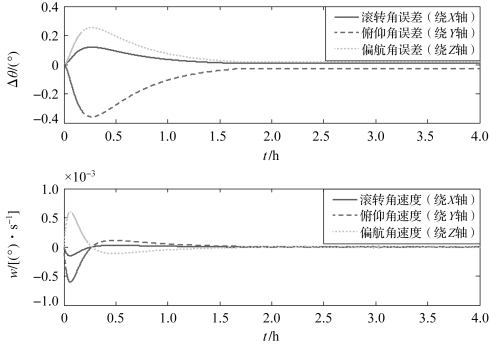
图3-39 刚性太阳帆姿态稳定控制的姿态变化图
由刚性太阳帆姿态稳定控制的姿态变化图可知，开始时，由质心压心差造成的光压干扰力矩起到主导作用，太阳帆姿态即三轴姿态角发生转动，均偏离了初始位置，在第0.27 h三轴姿态角误差同时达到最大值，然后在姿态控制系统作用下缓慢回到初始位置附近，滚转角在第1.5 h左右进入稳态，俯仰角和偏航角在第1.65 h左右后进入稳态，三轴稳态误差分别是0.01°、0.03°、0.02°。姿态角速度在光压干扰力矩作用下从零初始状态开始增大，在第0.06 h达到峰值，也是在1.65 h后进入稳态，滚转轴、俯仰轴和偏航轴三轴角速度回到零状态附近，即不再发生转动。
下面研究刚性太阳帆姿态机动控制。以斜坡信号加载在太阳帆控制系统上，参考输入始于0 h，仿真时间为4 h，仿真结果如图3-40所示。
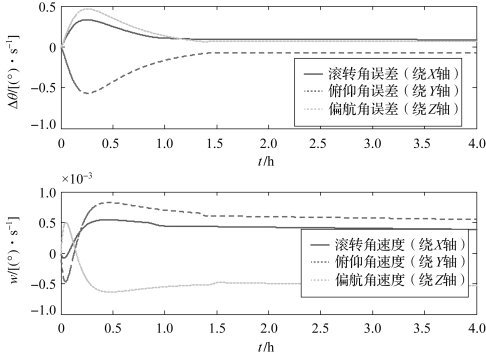
图3-40 刚性太阳帆姿态机动控制的姿态变化图
由刚性太阳帆姿态机动控制的姿态变化图可知，太阳帆在姿态控制系统和光压干扰力矩共同作用下，从初始位置上开始偏离，刚开始逐渐斜坡信号，三轴欧拉角偏差在第0.25 h分别达到最大值0.33°、-0.57°和0.47°，在第1.5 h左右进入稳定跟踪信号状态，与信号的误差分别保持在0.09°、-0.07°和0.07°。从角速度变化子图可以看出，三轴角速度刚开始变化模式同刚性太阳帆的姿态稳态，说明刚开始是光压干扰力矩起着主导作用，之后在第1.5小时左右进入稳态，三轴稳态角速度分别为4×10-4°／s、6×10-4°／s和-5×10-4°／s。
通过对刚性太阳帆模型的姿态稳定控制仿真和姿态机动仿真，可以得出如下结论：
（1）所设计的执行机构和控制器能够进行该模型的姿态控制，都能够满足所要求的姿态指向精度和稳定度；
（2）该套控制系统能够抑制质心压心产生的干扰力矩；
（3）姿态稳定控制时姿态稳定度明显优于姿态机动控制。
2.“中心刚体＋挠性附件”动力学模型
十字中心刚体
通过太阳帆的有限元模态仿真分析显示太阳帆的大柔性主要体现在对称分布的四片柔性材料帆面结构上，太阳帆伸展臂振型位移相对于太阳帆振型位移基本为零，相当于刚性体，所以在中心刚体加挠性附件的模型中，将中心箱体与伸展臂作为十字中心刚体模型。
质量杆挠性附件假设
为了逐步研究太阳帆帆面挠性特性对太阳帆姿态控制的影响，同时简化太阳帆模型，首先将每块帆面按质量等效原则简化为1根挠性杆件，以期通过杆的挠性特性来反映帆面的挠性特性。质量等效原则为：将每块帆面沿着斜边中线等分成10份，10份帆面按照从小到大的顺序比例关系为：1∶3∶5∶7∶9∶11∶13∶15∶17∶19，按照此比例将帆面质量分配给每一份对应的等长度斜边中线线段，最终等效为总长度为斜边中线长的变截面变质量挠性杆。每一块帆面均按此等效原则简化为总质量与帆面总质量相等、沿帆面斜边方向具有同样质量变化特性的质量杆挠性附件。太阳帆的十字中心刚体加质量杆挠性附件有限元模型如图3-41所示。
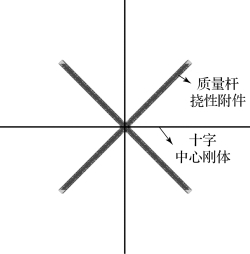
图3-41 十字中心刚体加质量杆挠性附件
帆面挠性附件假设
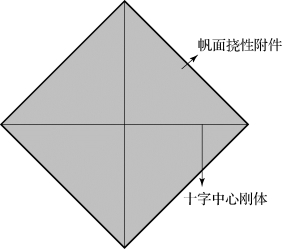
帆面挠性附件与十字中心刚体的连接方式为：帆面的两个45°角点与邻近的伸展臂自由端连接，帆面90°角点与中心箱体中心连接。为了更加贴近实际状态，有限元模型采用RBE2单元对连接处进行模拟，保证了帆面节点与伸展臂节点在三向位移坐标上的一致性，同时又不对3个转动自由度做任何约束，如图3-42所示。
图3-42 帆面挠性附件
三种模型对比
由于篇幅限制，这里只给出上述两种中心刚体加挠性附件太阳帆姿态动力学模型的斜坡信号姿态角误差图（图3-43），并与刚体模型进行对比，不再单独给出姿态角跟踪曲线图、执行机构速度图和模态坐标图。
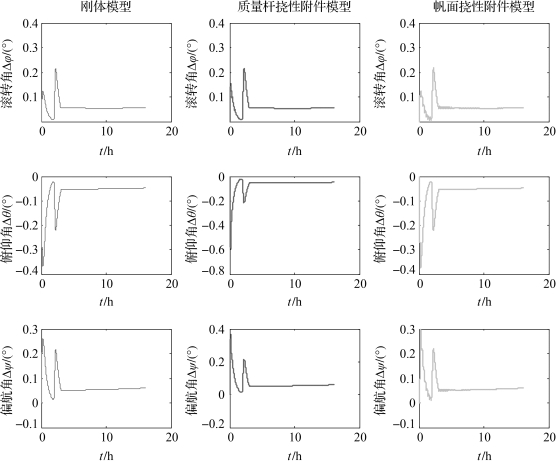
图3-43 三种太阳帆姿态动力学模型在斜坡信号下的姿态角误差
根据上图所示结果，与刚体模型相比，考虑太阳帆帆面柔性特性的两种模型，其姿态角误差曲线的超调量均有所增加，增加百分比为20%～50%，并且误差曲线的小幅抖动更加剧烈。可以看出后两种模型一定程度上能够体现太阳帆帆面挠性振动对太阳帆姿态运动的影响。分析比较上面太阳帆三种姿态动力学模型可以得出如下结论：
•刚体模型模型简单，适合控制律设计和分析。缺点是忽略了大型太阳帆航天器的柔性特性，特别是帆面挠性振动对姿态控制的影响，只适合太阳帆初步设计。
•质量杆挠性附件模型和帆面挠性附件模型具有较为简单的动力学模型，便于星上进行控制设计，可以用于大型柔性太阳帆姿态动力学仿真分析，其仿真结果具有一定的工程参考价值。与刚体模型相比，两种模型均不同程度地体现了太阳帆航天器柔性特性。
3.太阳帆全柔性动力学模型
太阳帆模型由刚性模型换成挠性模型，其他仿真条件不变，同样进行姿态稳定控制和姿态机动控制，然后对比模型对控制的影响。
从图3-44中可以看出，挠性太阳帆欧拉角变化过程同刚性太阳帆几乎完全一样，三轴稳态误差同样分别是0.01°、0.03°、0.02°。而角速度变化形式有些区别，表现在，由于光压干扰力矩存在，刚开始时挠性太阳帆控制系统动作导致角速度距离振荡，说明此时挠性振动占主导因素。之后区别大致形式如同刚性太阳帆，但挠性振动还是轻微影响到角速度，最后挠性振动不再对角速度产生影响。挠性振动影响姿态控制执行机构也主要在控制初期，使得执行机构速度出现抖动，滑块速度甚至达到了极限50 cm／s。
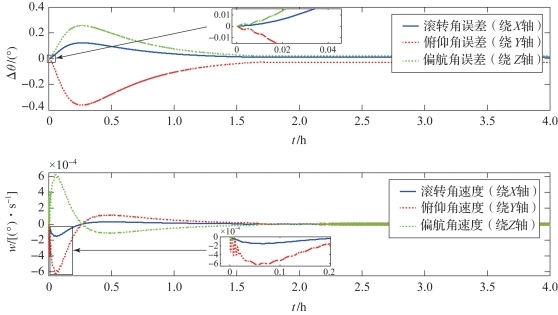
图3-44 挠性太阳帆姿态稳定控制的姿态变化图（书后附彩插）
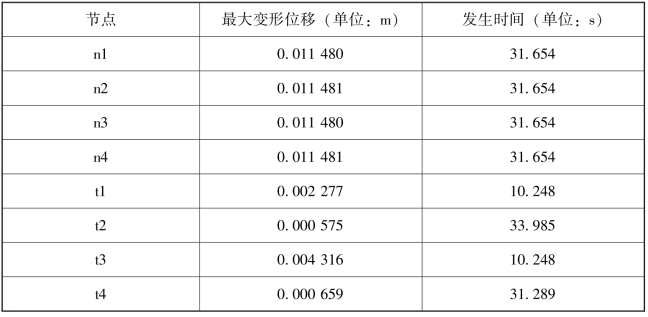
从图3-45帆中点和尖端点的变形曲线图可以看出，姿态控制的初期激起的振动变形比较剧烈，到0.5 h后基本趋于平稳。而从帆中点和尖端点最大变形表（表3-15）中可以看出，帆面最大变形比尖端点最大变形要大一到两个量级，帆中点最大变形的大小和发生时间是一致的，在31.654 s的最大变形都是0.011 48 m，而尖端点t1和t3比尖端点t2和t4大一个量级，并且发生时间也不同。
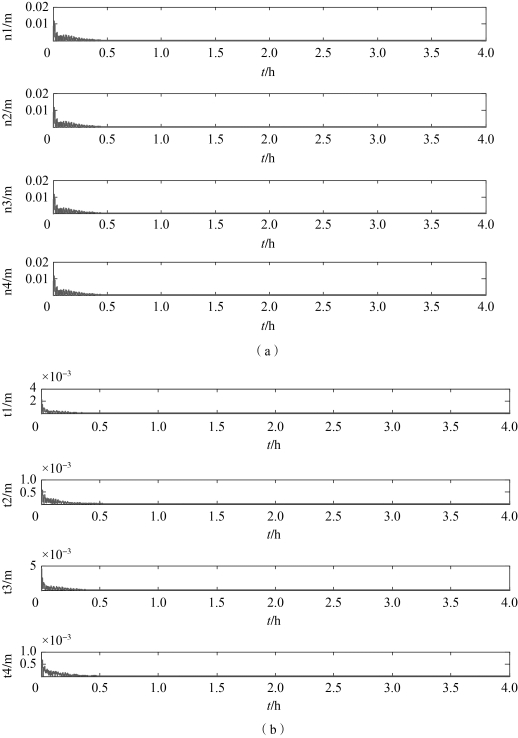
图3-45 挠性太阳帆姿态稳定控制的特征点变形曲线图
（a）帆中点；（b）尖端点
表3-15 挠性太阳帆姿态稳定控制的特征点最大变形表
姿态机动控制的仿真结果如图3-46所示，可以看出，挠性太阳帆欧拉角变化过程同刚性太阳帆几乎相同，三轴稳态误差同样分别是0.09°、-0.07°、0.07°，比姿态稳定控制的误差大。而角速度变化形式有些区别，表现在由于光压干扰力矩存在，刚开始时挠性太阳帆控制系统动作导致角速度距离振荡，说明此时挠性振动占主导因素。之后区别大致形式如同刚性太阳帆，但挠性振动还是轻微影响到角速度，最后挠性振动不再对角速度产生影响。
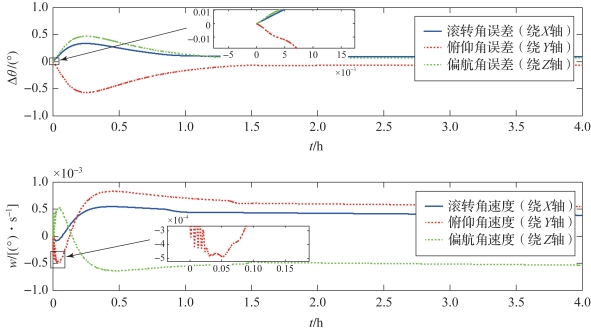
图3-46 挠性太阳帆姿态机动控制的姿态变化（书后附彩插）
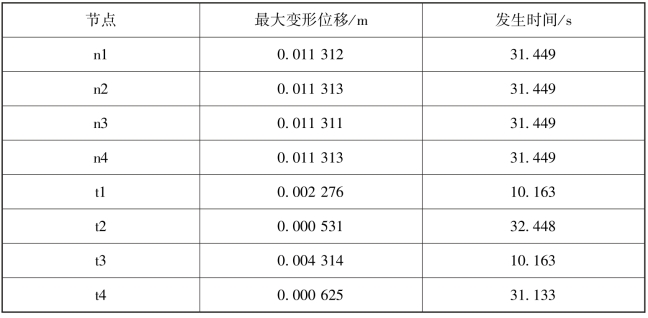
从帆中点和尖端点最大变形表（表3-16）中可以看出，帆面最大变形比尖端点最大变形要大一到两个量级，帆中点最大变形的大小和发生时间是一致的，都是在31.449 s的最大变形基本一致，而尖端点t1和t3比尖端点t2和t4大一个量级，并且发生时间也不同。
表3-16 挠性太阳帆姿态机动控制的特征点最大变形表
通过对太阳帆全柔性动力学模型进行姿态稳定控制和姿态机动控制仿真，可以得出如下结论：
•所设计的执行机构和控制器能够进行太阳帆全柔性动力学模型的姿态控制，都能够满足所要求的姿态指向精度和稳定度；
•无论在姿态稳定控制过程中还是在姿态机动控制过程中，代表太阳帆整体变形情况的8个特征点变形都很小，说明太阳帆的挠性变形对姿态控制的影响较小。