3.3.5 不同参数的影响分析
1.推进效率的影响
考虑到太阳帆的柔性、变形等影响，一般会使真实太阳帆的推进能力有所减弱，并且这种影响不是固定的而是时变的，需要对太阳帆的结构、姿态、轨道进行耦合分析才能精确得到，并且定量的影响作用是有个体化差异的，与太阳帆的形状、位置、姿态等特性和状态有紧密关系。在轨道设计阶段，无法考虑这种耦合的时变影响，否则会给轨道设计带来极大困难，并且无法从本质上分析解决轨道设计的关键难题，因而在轨道设计时，一般把这种时变的影响平均化地处理为推进效率的等效固定损失，计算时将太阳帆的光压因子选为某固定推进效率下的结果。下面将针对本任务提出的200 kg、160 m见方的太阳帆，分析不同的推进效率对轨道设计的影响。选取不同推进效率实际上是改变了太阳帆的推进能力，下面的分析将基于相同的探测目标和约束条件，定量地分析不同推进效率对轨道设计结果的影响。
前文给出的标称轨道设计结果是基于推进效率为65%，即β＝0.126 5的前提下的，实际上此效率值相对较小，是考虑了较低性能的太阳帆情况。对于不同的推进效率η，太阳帆的光压因子β和对应的特征加速度κ如表3-7所示。
表3-7 不同推进效率对应的光压因子与特征加速度
同样地，探测目标仍然为地球出发→Britta交会→Nicholson交会→Vesta交会，由于最优控制律决定了在两颗目标之间的姿态角不连续，上文给出的连续性处理是为了工程上姿态控制实现的便利性，并且该结果是在初始计算得到的交会结果基础上在到达目标附近进行了姿态微调，对整个飞行时间和整体的姿态变化规律影响不大，因而这里只对比交会情况下的初始设计结果。从地球出发的可选窗口时刻仍然在2020年1月1日至2023年1月1日的3年之间优化选择，各星的参考轨道根数如表3-2所示，其他约束条件与上文算例相同，只改变光压因子的大小得出推进效率与飞行时间的关系曲线如图3-21所示。
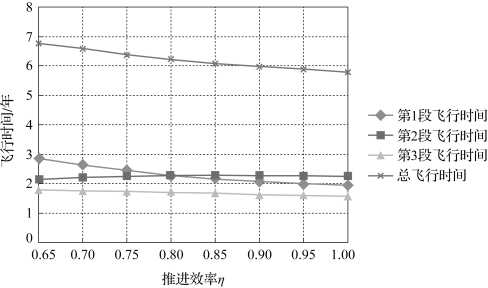
图3-21 推进效率与飞行时间的关系曲线
从图中可以看出，随着推进效率的增加，主要影响了地球到第1颗目标小行星Britta的飞行时间，第1段飞行时间会逐渐缩短，并且减短效果比较明显，而第2、3段由于第1段飞行时间的变化，目标之间的相位差受到影响，不同推进效率之间的飞行时间长短变化不明显，但由于第1段时间缩短较多的影响，总共的飞行时间也呈缩短的趋势。
但是需要指出的是，即使对于相同的探测目标序列，在出发窗口有一定限制的前提下，太阳帆推进性能的提升并不一定意味着任务飞行时间的缩短，这是因为推进能力高的太阳帆需要的最优窗口可能并不在有限制的时间窗口内，此时有限制的时间窗口可能对应了高性能太阳帆一个比较“坏”的相对相位关系，甚至造成更长的任务飞行时间。当然，一般情况下，当时间窗口的限制放宽时，推进性能的提升对于缩短任务时间的规律是存在的。
从另一方面考虑，对于不同的推进效率（即光压因子不同），太阳帆的加速性能不同，在任务顶层的探测目标选择时可能结果也并不相同，甚至一种特定的推进性能即对应一种优化结果，但由于本文中上述讨论利用的不同的太阳帆推进性能之间差别并不很大，因而对顶层设计的结果影响并不很大，不同的推进性能其顶层设计筛选结果差别也不会很大。
2.锥角约束的影响
上文相关分析均是基于锥角不受约束的情况。实际中，随着锥角α的不断增大，当α的值超过某一角度值而接近90°的范围内，光压力不再按照α的余弦函数平方分布，而是接近于0推力。另外，太阳帆展开后一般具有巨大的反射帆膜，要实现大面积帆飞行器的姿态调整，相比于一般航天器对姿态控制系统提出了更高的要求。因此，一方面为了避免过大锥角时无推进力的情况；另一方面为了姿态控制系统实现的便利性，工程实际中会要求在轨道优化设计时人为限定控制角的范围，即认为控制锥角（太阳帆的法线与光线夹角）只能在有限的范围内变化。
假设工程要求的锥角变化范围在0°至某一锐角范围内，即最大的α不能超过90°，则容许控制集如下式所示
下面讨论控制锥角范围受限的情况下的最优控制律。当锥角受约束时，最优条件仍如式（3-36）所示，即
与不受约束的情况不同的是，J2对α的驻值点有可能不落在锥角约束的范围内。因此最优控制律要根据无约束情况中临界值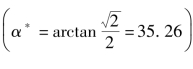
具体判断。当最大约束锥角αmax大于等于35.26°时，最优控制律为
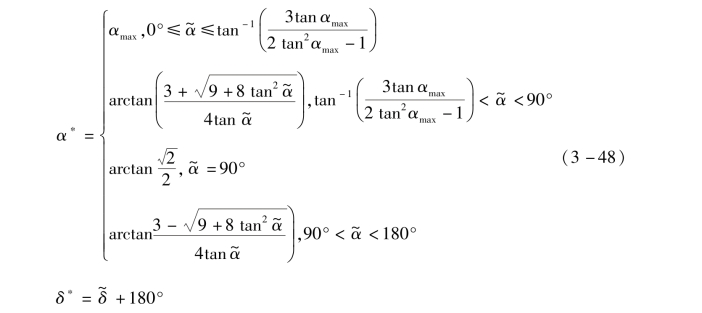
当最大约束锥角αmax小于35.26°时，最优控制律为
图3-22给出了不同最大容许值αmax下的最优控制角α*随主矢量方向角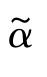
的变化关系。
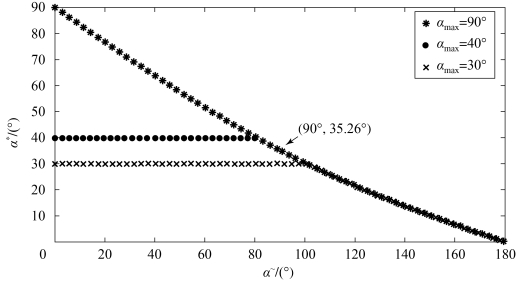
图3-22 不同最大锥角约束值αmax下的最优控制律
值得指出的是，除了最优控制律不同外，锥角受约束情形与无约束情形的求解步骤相同：仍采用协态初值归一化技术，利用非线性算法程序包求解由终端状态式（3-22）、静态条件式（3-25）和式（3-26）及归一化条件式（3-45）组成的打靶方程。计算时三段转移轨道分别优化，其中第一段（地球到Britta）中出发时刻是一个优化变量，第二、三和四段中的出发时刻为上一段的到达时刻，不再是优化变量，相应的关于初始时刻的打靶方程也不再采用。
利用锥角受约束的最优控制律进行太阳帆探测3颗主带小行星任务。这里选择的探测序列为从地球出发，依次交会小行星Britta、Nicholson和Vesta。考虑的最大约束锥角分别为90°（即对应无约束情形）、60°、50°和45°四种情形。四种情形下太阳帆的最优控制律如图3-23所示。具体地，四种情形下太阳帆交会的飞行时间如表3-8所示。
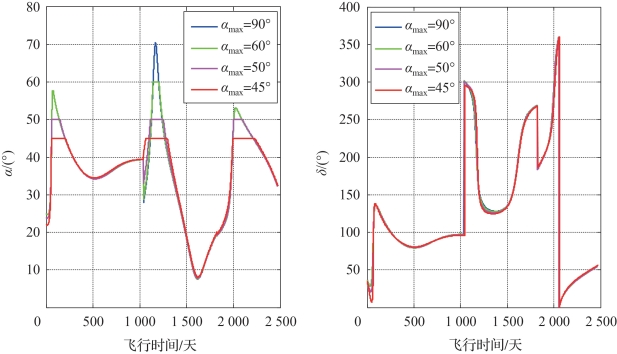
图3-23 不同锥角约束时太阳帆的时间最优控制律（书后附彩插）
表3-8 四种情形下太阳帆交会三颗小行星的时间节点
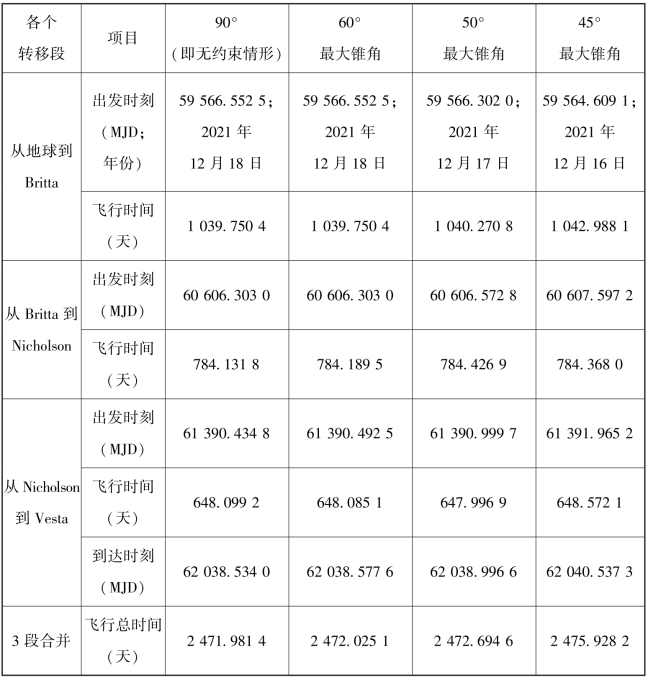
从控制律响应图和交会数据表中可以看出，最大约束角度越小，太阳帆完成交会所需时间越长，这也是符合预期的。具体到本任务，一定的锥角约束对于本任务总飞行时长的影响并不显著。锥角约束对任务时间的影响与具体的交会目标有关，总的来说，当无约束的最优控制律中超过所取约束角度的时段占的比例较小时，锥角约束对飞行时间的影响并不显著，反之则影响显著。
可以设想的是，当最大锥角约束变得很小时，飞行时长可能会变得较大而不符合任务的飞行总时间要求。实际的仿真计算中发现，由于非线性方程对初值的敏感性，当给定的最大锥角逐渐变小时，打靶方程的解的收敛难度可能会变得很大。因此，结合工程上能实现的锥角机动范围，给出了如上几组锥角约束的情形。