3.2.2 动态自聚合主题模型（SADTM）的建立
动态自聚合主题模型（SADTM）将每个长文本看作由短文本片聚合而成。在长文本中，每个短文本是可观测的，而短文本的分配分布关系是未知的。短文本被表示成{R，S}，其中，短文本R是无序且可观测到的，聚合文档S是未知的。引入动态狄利克雷多项分布来建模社交网络主题的动态性，通过联合先前时间片的主题分布和新到来的流数据来建模当前的主题分布。
假设不同的时间片下，社交网络主题动态变化，时间片可以形式化表示为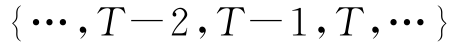
，时间片的间隔可以被设置为一天、一周或一个月等。社交网络的主题分布表示为θt，k，词分布表示为ϕt，v。为了进一步解决社交网络上下文稀疏性问题，通过直接建模词对以生成更多的词共现信息。其中，词对是从相同主题生成的两个独立的词。在时间片t，通过SADTM模型来捕获主题的多项分布θt，k和词分布ϕt，v，并通过采样过程来计算主题分布θt，k和词分布ϕt，v。动态自聚合主题模型（SADTM）采用的主要变量或标号如表3-1所示。
对于当前的时间片t，通过当前的词分布ϕt，v来采样词对（w i，w j），并推断当前的主题分布θt，k。动态自聚合主题模型（SADTM）的模型图如图3-2所示，其中阴影部分表示可以观测到的值。
表3-1 SADTM模型中使用的变量或标号
从图3-2可以看出，相邻时间片的主题分布构成了依赖关系，后一个时间片的主题分布依赖于先前时间片的主题分布。如果在t时刻到来的数据没有改变，那么t时刻的主题分布将与t-1时刻的主题分布一致，只有当主题有新变化时，SADTM模型能够动态地捕获当前的最新的主题分布。
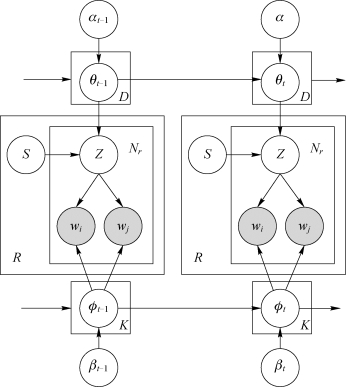
图3-2 动态自聚合主题模型（SADTM）的模型图
利用先前的主题分布和当前的狄利克雷先验构建一个新的狄利克雷先验。具体实现通过构建准确值集合来完成，准确值的形式化表示为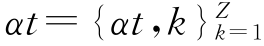
，基于该表示，令当前的主题分布θt，k依赖于先前的主题分布θt-1，k。SADTM模型中的准确值αt，k表示主题的持久性，即当前时间t的主题z与先前时间t-1主题相比的显著性。由于主题分布是共轭先验，利用吉布斯采样算法来推断主题分布，如式（3-1）所示：
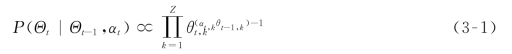
通过先前时间片t-1的词分布ϕt-1推断当前时间片t的词分布ϕt。其中，βt，z表示词的持续性，即在当前时间片词w分配给主题z与在先前时间片相比的持续性，如式（3-2）所示：
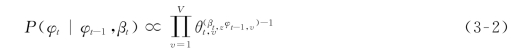
假设在t-1时刻，主题分布和词分布是已知的，动态自聚合主题模型（SADTM）建模当前的主题分布和词分布依赖于先前的主题分布θt-1和词分布ϕt-1。对于t=0初始时刻，分别设置主题分布和词分布的初值为θ0，k=1/K和φ0，V=1/V。
由于SADTM模型中涉及多个隐变量和未知参数，因此，需要对隐变量和未知参数进行推导。采用吉布斯采样算法来推导隐变量和未知参数。吉布斯采样算法的核心思想是交替估计后验采样的随机变量，其中，每个随机变量基于其他随机变量的分配进行采样。
在动态自聚合主题模型（SADTM）中，利用吉布斯采样算法交替采样聚合文档分配S以及主题Z，得到如式（3-3）所示的条件分布：
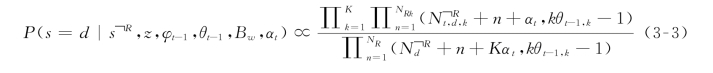
其中，N R，k表示在短文本R中词对分配给主题Z的数量，N t，d，k表示在聚合文档d中词对分配给主题Z的数量。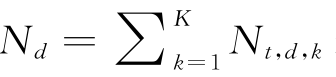
表示在聚合文档d中词对的总数量，N R表示在短文本R中词对的总数量，
R表示除去短文本R的计数。
利用链式规则采样主题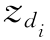
，得到如式（3-4）所示的条件分布：
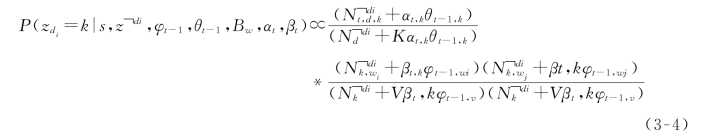
其中，w i是聚合文档d中的第i个词，N k，w表示词w分配给主题Z的总数量，di表示不包含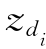
的计数。
利用最大联合似然方法，可以获取到αt，k和βt，k。通过使用定点迭代方法来计算最大联合似然，αt，k和βt，k，的计算分别如式（3-5）和式（3-6）所示：
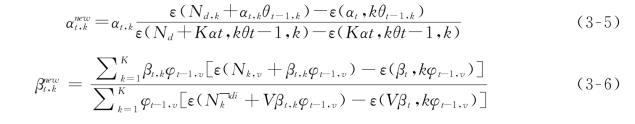
其中，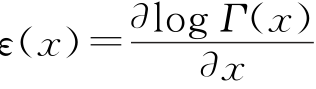
表示Digamma函数。