1.2 n阶行列式
1.2 n阶行列式
在1.1节，介绍了二阶、三阶行列式的定义. 在1.2节中，将根据二阶、三阶行列式的规律引出n阶行列式的定义. 首先，介绍全排列的相关知识.
1.2.1 全排列与逆序数
把n个不同的元素排成一列，称为这n个元素的全排列（也简称排列）. n个不同的元素所有可能的排列种数，称为全排列数，通常用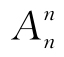
表示. 下面来给出
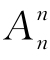的计算公式.
从n个不同元素中任取一个放在第一个位置上，有n种取法；从剩下的n-1个元素中任取一个放在第二个位置上，有n-1种取法；这样递推下去，直到最后只剩下一个元素放在第n个位置上，只有1种取法. 于是
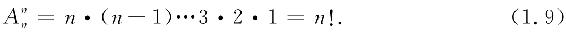
因此，n个不同元素的全排列数为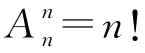
.
例如，用1，2，3三个数字，可以组成多少个没有重复数字的三位数？
这个问题相当于把3个数字分别放在百位、十位与个位上，有几种不同的放法？由式（1.9）可知，共有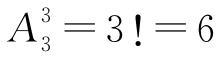
种放法. 事实上，百位上可以从1，2，3三个数字中任选一个，所以有3种放法；十位上只能从剩下的两个数字中选一个，所以有两种放法；而个位上只能放最后剩下的一个数字，所以只有1种放法. 因此，共有3×2×1=6种放法.
这6个不同的三位数分别是：
123，132，213，231，312，321.
对于n个不同的元素，先规定各元素之间有一个标准次序（例如n个不同的自然数，可规定由小到大为标准次序），于是在这n个元素的任一排列中，当某两个元素的排列次序与标准次序不同时，就称为有一个逆序. 一个排列中所有逆序的总数称为这个排列的逆序数.
一般地，n个自然数1，2，…，n的一个任意排列记作p1p2…pn，如果比pi大的且排在pi前面的元素有ττi个，就说元素pi的逆序数是τi.全体元素的逆序数之和
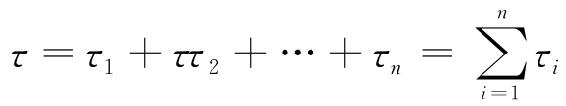
即是这个排列的逆序数.
例1.4 求排列43512的逆序数.
解 在排列43512中，4排在首位，逆序数为0；3的前面比3大的数有一个“4”，故逆序数为1；5是最大的数，逆序数为0；1的前面比1大的数有3个，即“4，3，5”，故逆序数为3；2的前面比2大的数有3个，为“4，3，5”，故逆序数为3；于是这个排列的逆序数为
τ-0+1+0+3+3-7.
逆序数为奇数的排列称为奇排列，逆序数为偶数的排列称为偶排列. 如例1.4中的排列43512就是一个奇排列.
1.2.2 对换
为研究n阶行列式的需要，我们再来讨论对换的概念以及其与排列奇偶性的关系.
将一个排列中任意两个元素的位置对调，其余元素不动，而得到一个新排列的过程称为对换. 若对换的是相邻的两个元素，则称为相邻对换.
排列43512可由排列34512进行一次相邻对换得到，也可由排列13542进行一次不相邻的对换得到. 可知排列34512和排列13542都是偶排列，而排列43512是一个奇排列，可见进行一次对换（无论相邻与否）将改变排列的奇偶性. 可得出下面的基本事实：
定理1 一个排列进行一次对换，排列改变奇偶性一次.
证 先证相邻对换的情形.
设排列为a1…alabb1…bm，对换元素a，b，变为a1…albab1…bm.显然，a1…al；b1…bm这些元素的逆序数经过a，b对换后并不改变，改变的只是元素a，b的逆序数，当a<b时，经对换后a的逆序数增加1，而b的逆序数不变；当a>b时，经对换后a的逆序数不变，而b的逆序数减少1. 因此，不论是增加1还是减少1，排列a1…alabbl…bm与排列a1 … albab1…bm的奇偶性不同.
再证一般对换情形.
设排列为a1…alab1…bmbc1…cn，将元素b作m次相邻对换，变成排列a1…alabb1…bmc1…Cn，再将元素a作m+l次相邻对换，变成排列a1…a1bb1…bmac1…cn.于是可知排列a1…alab1…bmbc1…cn经2m+1次相邻对换变成排列a1…albb1…bmac1…cn，所以这两个排列的奇偶性相反.
推论 奇排列变成标准排列的对换次数为奇数，偶排列变成标准排列的对换次数为偶数.
证 由定理1知，对换的次数就是排列奇偶性的变化次数，而标准排列是偶排列（逆序数为0），因此，可知推论成立.
1.2.3 n阶行列式
为了给出n阶行列式的定义，先来回顾一下三阶行列式的结构. 三阶行列式的定义为式（1.8），即
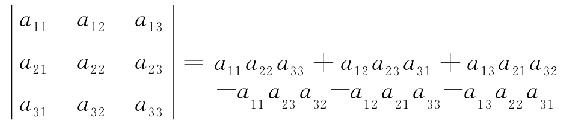
容易看出：
（i）式（1.8）右边的每一项都恰是位于不同行、不同列的3个元素的乘积. 因此，式（1.8）右边的任一项除正负号外可以写成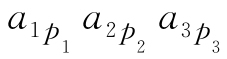
.这里第一个下标（行标）排成标准次序123，而第二个下标（列标）排成p1p2p3，它是1，2，3这3个数的一个全排列，这样的排列共有3!=6种，对应式（1.8）右边共有3!=6项.
（ii）各项的正负号与列标排列的对应情况：
取正号的三项列标排列是：123，231，312；
取负号的三项列标排列是：132，213，321.
易知前3个排列都是偶排列，而后3个排列都是奇排列. 因此各项所取的正负号可以表示为（-1）τ，其中，τ为列标排列p1p2p3的逆序数.
于是，三阶行列式可以写成
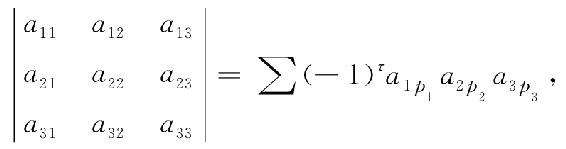
其中，τ为列标排列p1p2p3的逆序数，∑表示对1，2，3这3个数的所有排列p1p2p3对应的项求和.
以此类推，可把行列式推广到n阶的情形.
定义1 设有n2个数，排成n行n列的数表
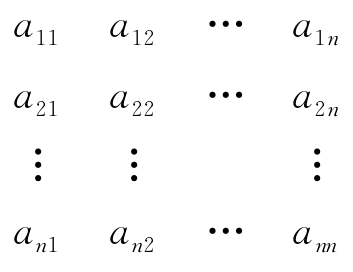
作出表中位于不同行不同列的n个数的乘积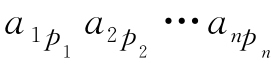
并冠以符号（1）τ，得到的项形如
其中，p1p2…pn为自然数1，2，…，n的一个全排列，x为这个排列的逆序数. 由于这样的排列共有n!个，因而形如式（1.10）的项共有n!项. 所有这n!项的代数和
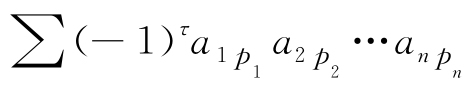
称为n阶行列式，记作
也简记作det（aij），其中aij称为行列式D的（i，j）元，即
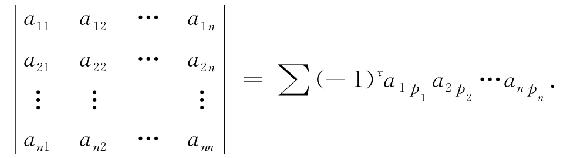
按此定义的二阶、三阶行列式，与1.1节中所用的对角线法则定义的二阶、三阶行列式是一致的. 特别当n=1时，一阶行列式|a|=a，注意不要与绝对值记号相混淆.
例1.5 计算下三角行列式：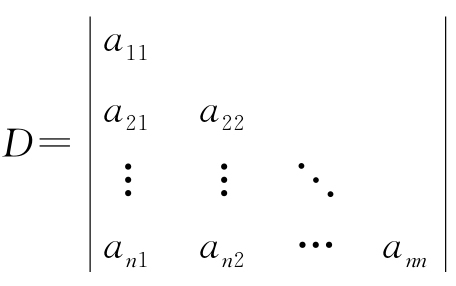
，
其中，未写出的元素全为零（以后均如此）.
解 在这个行列式中，当j>i时，aij=0，故D中可能不为0的元素aipi，其下标应满足pi≤i，即p1≤l，p2≤2，…，pn≤n.
在所有排列p1p2…pn中，能满足上述关系的排列只有一个自然排列12…n，所以D中可能不为0的项只有一项（-1）τa11a22…ann.此项的符号（-1）τ=（-1）0=1，所以
D=a11a22…ann，
即D等于主对角线上元素的乘积.
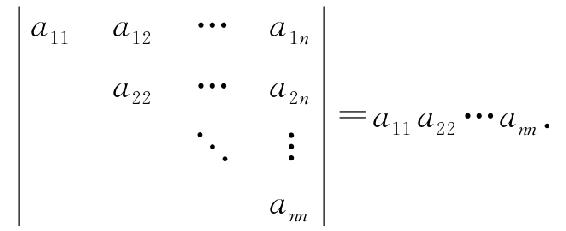
同理可得上三角行列式
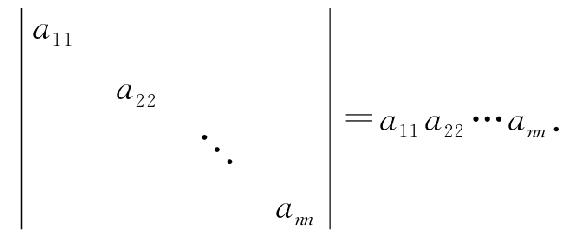
作为三角行列式特例的对角行列式（除对角线上的元素外，其他元素都为0，在行列式中未写出来）也有，
例1.6 证明行列式
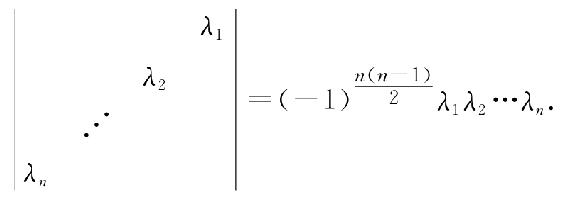
证 令λi=ai，n-i+1，则由行列式的定义
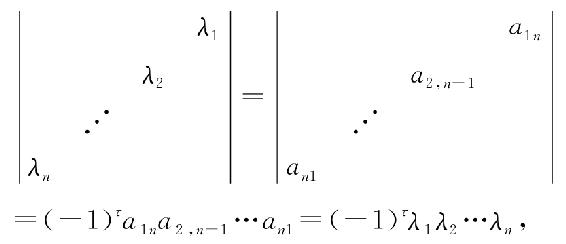
其中，τ为排列n（n-1）…21的逆序数，则τ=0+1+2+…+（n+1）=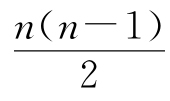
，故结论得以证明.
1.2.4 n阶行列式的其他定义形式
利用定理1，我们来讨论行列式定义的其他表示法.
对于行列式的任一项
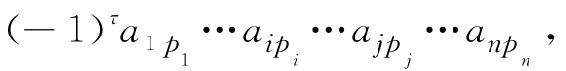
其中，l…i…j…n为自然排列，τ为排列p1…pi…pi…pn的逆序数，对换元素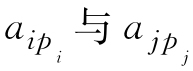
得
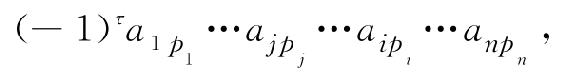
这时，这一项的值不变，而行标排列与列标排列同时作了一次相应的对换. 设新的行标排列l…i…i…n的逆序数为τ1，则τ1为奇数：设新的列标排列p1…pi…pi…pn的逆序数为τ2，则
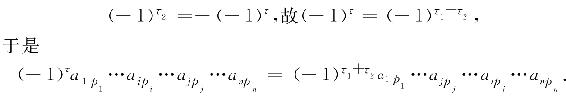
这说明，对换乘积中两元素的次序，从而行标排列与列标排列同时作了一次对换，因此，行标排列与列标排列的逆序数之和并不改变奇偶性. 经过一次对换如此，经过多次对换亦如此. 于是经过若干次对换，使列标排列p1p2…pn（逆序数为τ）变为自然排列（逆序数为0）；行标排列则相应地从自然排列变为某个新的排列，设此新排列为q1q2…qn，其逆序数为s，则有
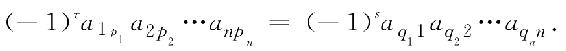
又若pi=j，则qj=i（即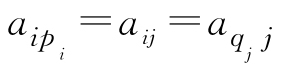
），可见排列q1q2…qn由排列p1p2…pn所唯一确定.
由此可得n阶行列式的定义如下：
定理2 n阶行列式也可定义为
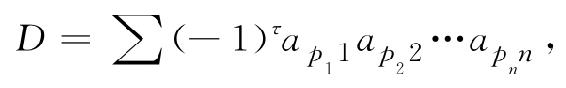
其中，τ为行标排列p1p2…pn，的逆序数.
证 按行列式定义有
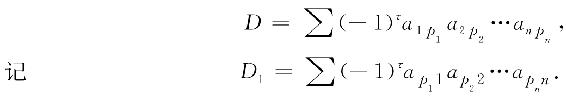
按上面的讨论可知：对于D中任一项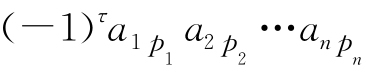
，总有D1中唯一的一项
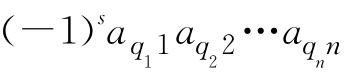与之对应并相等，反之，对于D1中的任一项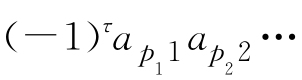
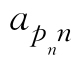，也总有D中唯一的一项
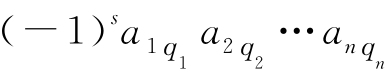与之对应并相等，于是D与D1中的项可以一一对应并相等，所以D=D1.
更一般的有，n阶行列式的定义如下：
定理3 n阶行列式可定义为
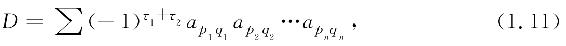
其中，p1p2…pn，q1q2…qn。分别为行标排列和列标排列，它们的逆序数分别为τ1，τ2 .
例1.7 判断在四阶行列式中，a21a32a14a43应取什么符号？
解 （1）按定义1计算.
因为a21a32a14a43=a14a21a32a43，而4123的逆序数为
τ=0+1+1+1=3，
所以，a21a32a14a43的前面应取负号.
（2）按定理3计算.
因为a21a32a14a43的行标排列2314的逆序数为
τ1=0+0+2+0=2，
列标排列1243的逆序数为
τ2=0+0+0+1=1，
τ1+τ2=3，为奇数，所以a21a32a14a43的前面应取负号.