6.3 正定二次型

6.3　正定二次型

二次型的标准形显然是不唯一的，但标准形中所含平方项的项数（即二次型的秩）是不变的. 不仅如此，在限定变换为实变换时，标准形中正系数个数也是不变的（从而负系数个数不变），也就是有下述结果存在：

定理2　（惯性定理）设有二次型f=XTAx，它的秩为r，有两个可逆线性变换

x=Cy及x=Pz，

使

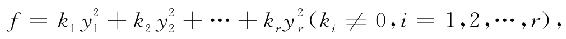
及

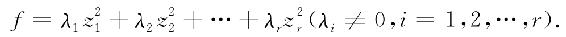
则k1，k2，…，kr中正数的个数与λ1，λ2，…，λr中正数的个数相等.（证明略）

在二次型f的标准形中，正系数个数称为二次型f的正惯性指数，负系数个数称为二次型f的负惯性指数.

在n元二次型中，比较常用的是二次型的标准形的n个系数全为正或全为负的情形.

定义3　设二次型f=xTAx，若对任何非零向量x，都有

（i）若f>0，则称f为正定二次型，并称对称矩阵A为正定矩阵；若f<0，则称f为负定二次型，并称对称矩阵A为负定矩阵；

（ii）若f≥0，则称f为半正定二次型，并称对称矩阵A为半正定矩阵；若f≤0，则称f为半负定二次型，并称对称矩阵A为半负定矩阵.

既不是正定二次型、半正定二次型也不是负定二次型、半负定二次型的二次型称为不定二次型，二次型的正定、半正定、负定、半负定或不定统称为二次型的正定性.

定理3　二次型f=xTAx为正定二次型的充分必要条件是：它的标准形中n个平方项的系数全为正，即它的正惯性指数等于n.

证　设可逆线性变换x=Cy使

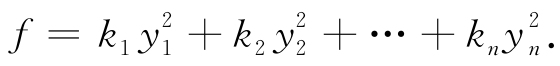
先证充分性. 设ki>0（i=1，2，…n），任取x≠0，则y=C-1x≠0，故

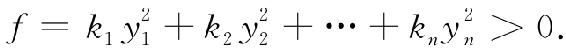
再证必要性. 用反证法，设有kt≤0，则取y=et（单位坐标向量），它的第t个坐标分量为1，有f（x）=f（Cet）=kt≤0，这与f正定矛盾，故ki>0（i=1，2，…，n）.

推论　对称矩阵A为正定矩阵的充分必要条件是：A的特征值全为正.

定义4　设A=（aij）n×n，称

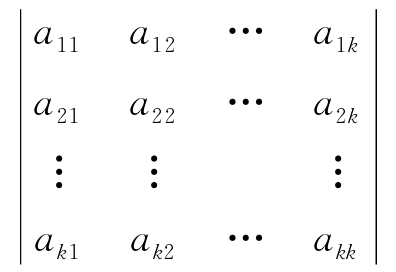
为A的k阶顺序主子式.

定理4　对称矩阵A=（aij）为正定矩阵的充分必要条件是：A的各阶顺序主子式都为正，即

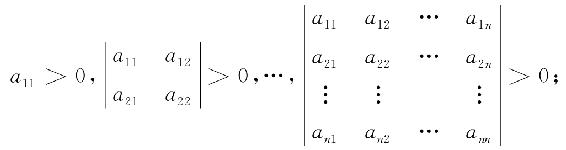
对称矩阵A=（aij）为负定矩阵的充分必要条件是：A的奇数阶顺序主子式都为负，而偶数阶顺序主子式都为正，即

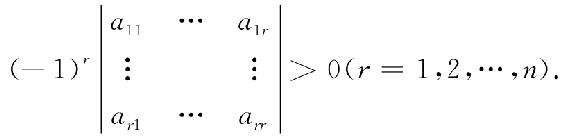
这个定理称为霍尔维茨（Hurwitz）定理，这里不予证明.

例6.4　判别二次型

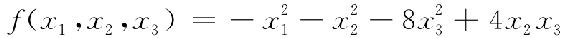
的正定性.

解　f的矩阵为

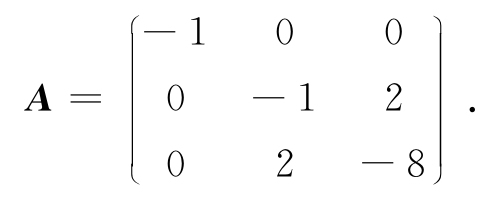
A的各阶主子式为：

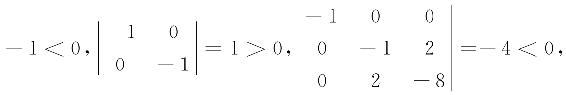
根据定理4可知二次型为负定的.

例6.5　λ为何值时，二次型

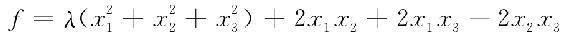
为负定的.

解　f的矩阵

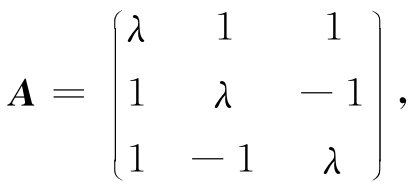
要f是负足的，则A的奇数阶顺序主子式小于零，偶数阶顺序主子式大于零，即

则λ<-1时，f是负定的.