习题参考答案

习题1

1.（1）-14；（2）2；（3）3abc-a3-b3-c3；（4）-2（x3+y3）.

2.（1）3；（2）14；（3）5；（4）18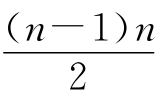；；（6）n（n-1）.

3.（1）6，8；（2）-a11a23a32a44，a11a23a34a42；（3）+，+；（4）a13a25a31a44a52，a13a25a32a41a54，a13a25a34a42a51

4.（1）900；（2）9；（3）4abcdef；（4）x2y2.

6.（1）-14；（2）0；（3）144.

7.（1）an-2（a2-1）；（2）[x-1+（n-1）a]（x-1-a）n-1；

（3）（a2a3…an）；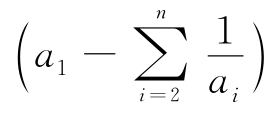

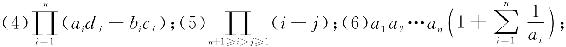
（7）（-1）n-1（n-1）2n-2.

8.（1）x=1，y=2，z=3；（2）x1=1，x2=2，x3=3，x4＝-1.

9. 3或-3.

习题2

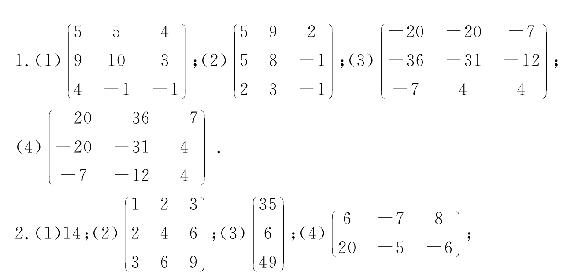
（5）a11x2+a22y2+a33z2+2a12xy+2a13xz+2a23yz；

（6）.

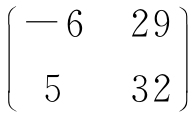3.（1）AB≠BA；

（2）（A+B）2≠A2+B2+2AB；

（3）（A-B）（A+B）≠A2-B2；

（4）（AB）2≠A2B2.

4. （1）取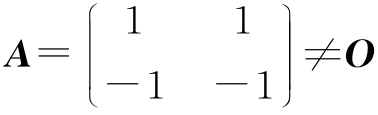，而A2=O；

（2）取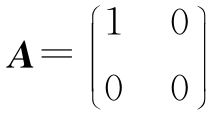，有A≠O，A≠E，而A2=A；

（3）取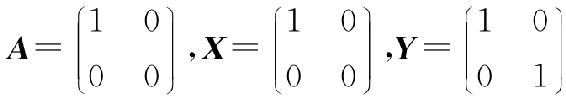，有X≠Y，而AX=AY.

5. .

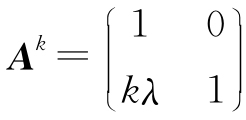习题3

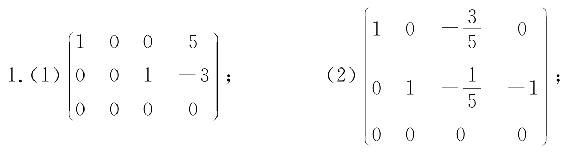
6. 当k=3时，R（A）=2；当k≠3时，R（A）=3.

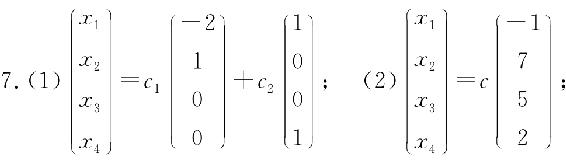
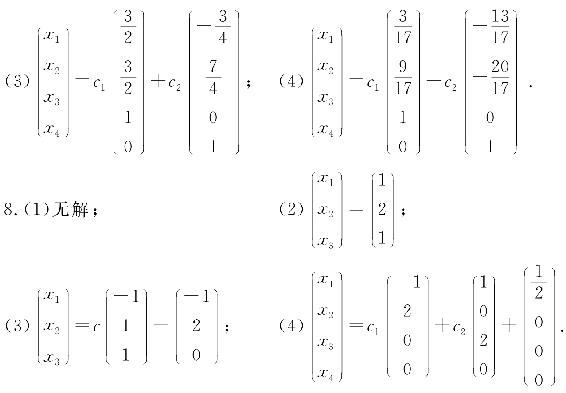
9. 当t＝-1时，方程组无解；

当t-1且t≠4时，方程组有唯一解；

当t=4时，方程组有无穷多解.

习题4

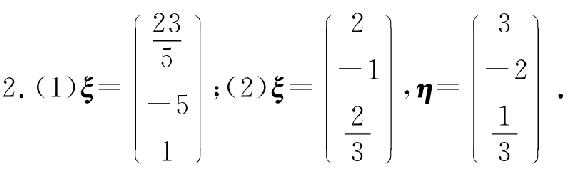
3. 当a≠1时，；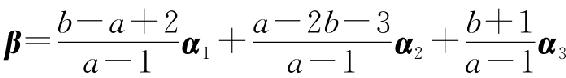

当a=1且b≠-1时，β不能由α1，α2，α3线性表示；

当a=1且b＝-1时，β=（-1+c）α1+（1-2c）α2+cα3（c为任意常数）.

6.（1）线性相关；（2）线性无关.

10.（1）秩为3，a1，a2，a3为最大无关组，a4=a1+3a2-a3，a5＝-a2+a3；

（2）秩为2，a1，a2为最大无关组，；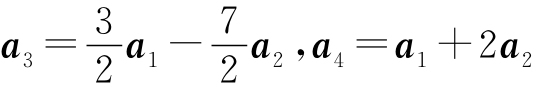

（3）秩为2，a1，a2为最大无关组，a3=a1+3a2，a4=2a1-a2，a5＝-2a1-a2.

11. a=2，b=5.

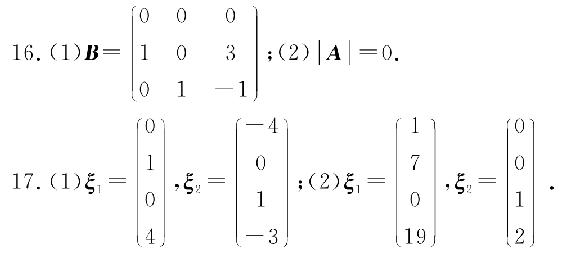
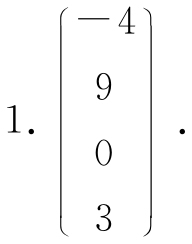
18.（1）ξ1=（5，-3，1，0）T，ξ2=（-3，2，0，1）T；

（2）a＝-1，x=k1（2，-1，1，1）T+k2（-1，2，4，7）T（k1，k2不全为零）.

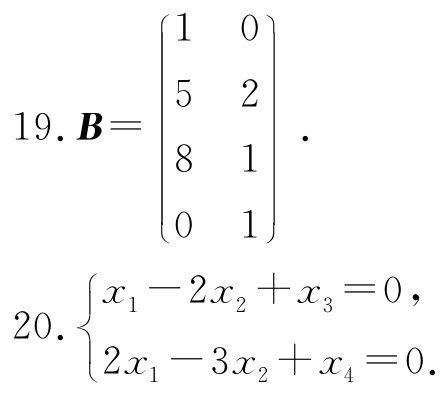
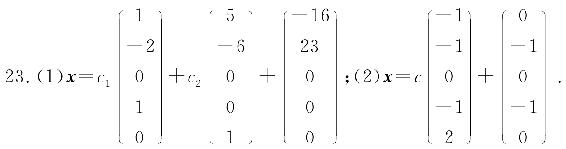
24.（1）当a=0，b为任意常数时，β不能由α1，α2，α3线性表示；

（2）当a≠0，且a≠b时，β可由α1，α2，α3唯一的线性表示，其表示式为

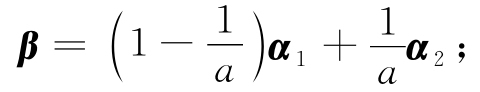
（3）当a=b≠0时，β可由α1，α2，α3线性表示，但表示不唯一，其表示式为

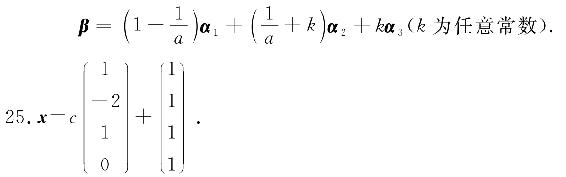
30. b1=2a1+3a2-a3，b2=3a1-3a2-2a3.

习题5

1. （1）-9；（2）.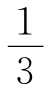

2. λ=-2，c=（-2，2，-1）T.

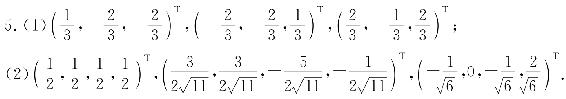
6. （1）是；（2）是.

7. （1）λ1=3，对应特征向量为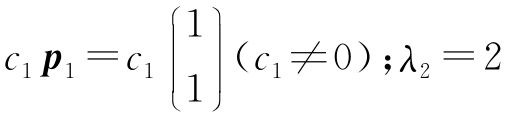，对应特征向量为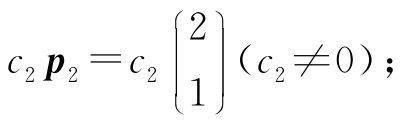

（2）λ1=λ2=2，对应特征向量为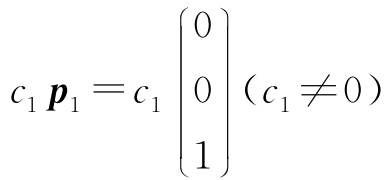；λ3=1对应特征向量为；

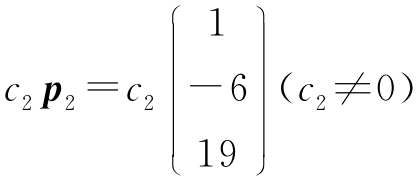（3）λ1=2，对应特征向量为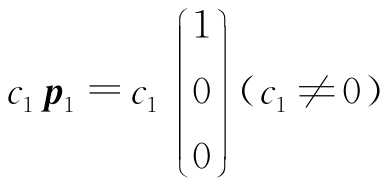； λ2=1对应特征向量为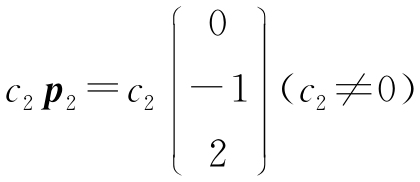；λ3＝0，对应特征向量为；

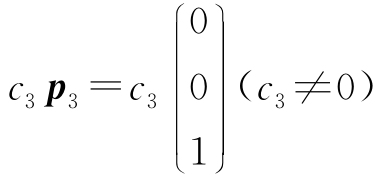（4）λ1=1，对应特征向量为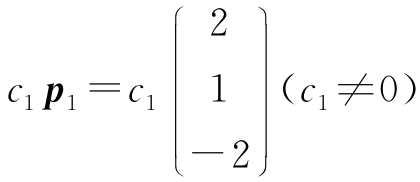；λ2＝-2，对应特征向量为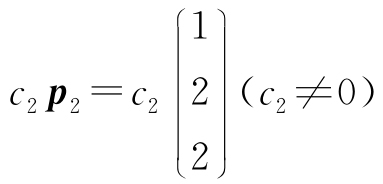；λ3=4，对应特征向量为.

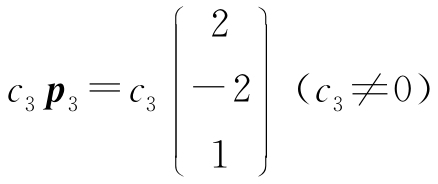12. 18.

13. 14.

14. x=3.

15. （1）a＝-3，b=0，λ＝-1.（2）略.

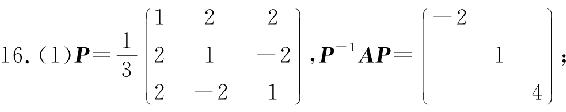
习题6

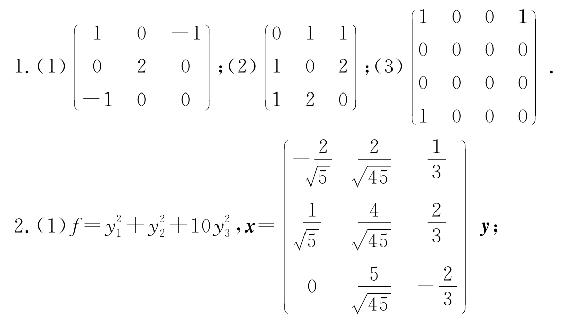
4.（1）正定；（2）正定.