6.2 配方法化二次型为标准形

6.2　配方法化二次型为标准形

除了用正交变换可以将二次型化为标准形外，还可以利用配方法化二次型为标准形. 具体做法是，先通过配方法将所有包含x1的项纳入一个完全平方项中，然后通过配方法将其余项中所有包含x2的项纳入一个完全平方项中，以此类推，即得标准形.

例6.2　利用配方法将二次型

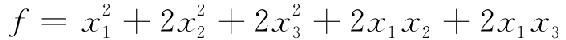
化为标准形，并求出相应的变换矩阵.

解　由于f中含X1的平方项，故把所有含x1的项归并起来，配方可得

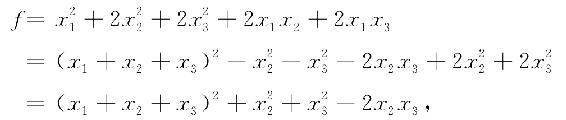
上式右端除第一项外已不再含x1，继续配方，可得

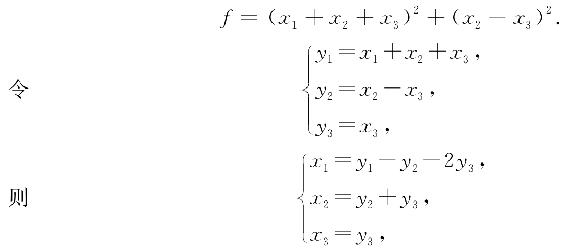
就把f化为标准形

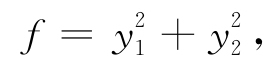
所用变换矩阵为

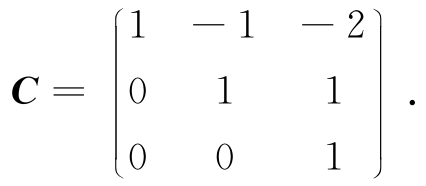
例6.3　利用配方法化二次型

f=2x1x2-2x1x3+2x2x3

为标准形，并求相应的线性变换.

解　f中不含平方项. 故令

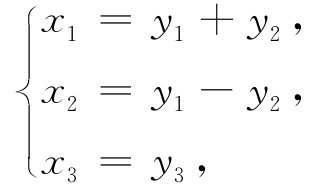
代入可得

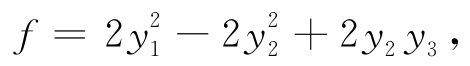
再配方，得

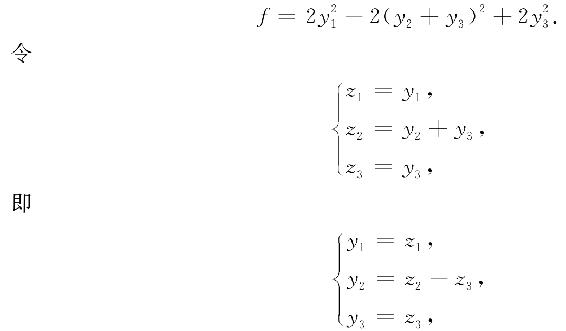
即有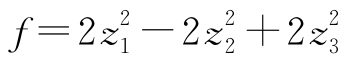. 而对应的线性变换为

x=C1y=C1（C2z）=（C1C2）z=Cz，

其中