2.3 逆矩阵

2.3　逆矩阵

在数的运算中，当a≠0时，有

aa-1=a-1a=1，

其中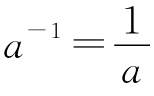，称为a的倒数（或称为a的逆）.

在矩阵的运算中，单位矩阵E相当于数的乘法运算中的1，那么对于矩阵A，如果存在矩阵“A-1”，使得

A-1A=AA-1=E，

则矩阵“A-1”可否称为矩阵A的逆呢？

定义11　设A为n阶方阵，若存在n阶方阵B，使得

AB=BA=E，

（2.3）

则称方阵A是可逆的，并称B是A的逆矩阵，简称逆阵，记作A-1=B.

由此定义可知，可逆矩阵一定是方阵，并且适合（2.3）式的矩阵B也一定是方阵；还可看出（2.3）式中A与B的地位是一样的，若矩阵A与B满足（2.3）式，则A与B都是可逆的，并且互为逆矩阵，即A-1=B，B-1=A.

定理1　若矩阵A可逆，则其逆矩阵唯一.

证　设B，C都是A的逆矩阵，则

AB=BA=E，AC=CA=E，

从而

B=EB=（CA）B=C（AB）=CE=C，

所以A的逆矩阵唯一.

为了讨论方阵可逆的充分必要条件及得出逆矩阵的计算方法，我们引入伴随矩阵的概念.

定义12　设A为n阶方阵，记

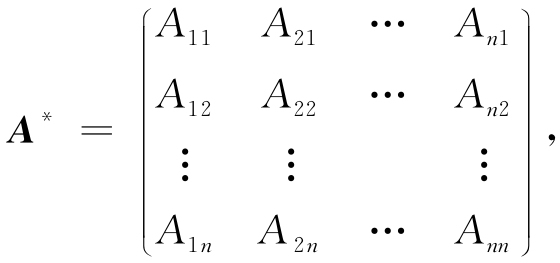
其中，Aij是|A|的元素aij的代数余子式，A*称为A的伴随矩阵.

定理2　设A*为A的伴随矩阵，则有

AA*=A*A=|A|E.

证　因为

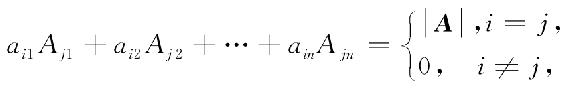
所以

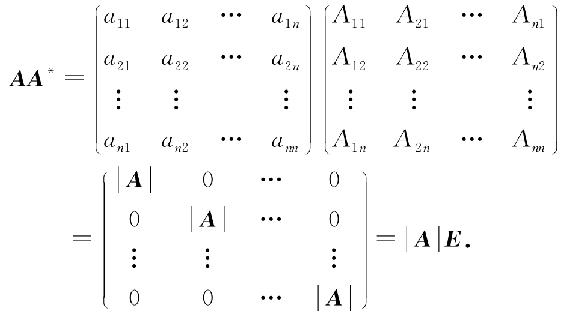
同理

A*A=|A|E.

于是

AA*=A*A=|A|E.

定理3　n阶方阵A可逆的充分必要条件是|A|≠0，且有

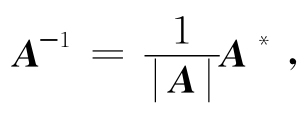
其中，A*为A的伴随矩阵.

证　先证必要性.

设A可逆，即A-1存在，则

AA-1=E，

于是|AA-1|=|A||A-1|=|E|=1，所以|A|≠0，

再证充分性.

根据定理2，有

AA*=A*A=|A|E，

又|A|≠0，故有

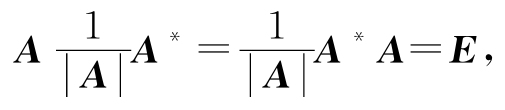
所以，根据逆矩阵的定义可知A可逆，且有

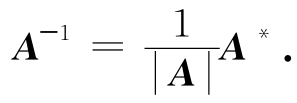
推论　设A，B都是n阶方阵，若AB=E（或BA=E），则A与B都可逆，且A-1=B，B-1=A.

证　因为AB=E，所以|AB|=|A||B|=|E|=1，由此可知|A|≠0，|B|≠0，于是根据定理3，A与B都可逆，且有

B=EB=（A-1A）B=A-1（AB）=A-1E=A-1，

A=AE=A（BB-1）=（AB）B-1=EB-1=B-1.

这个推论说明，要验证A是否可逆，只需验证AB=E或BA=E即可.

当|A|≠0时，我们称A为非奇异矩阵，否则成为奇异矩阵，由上面定理知，可逆矩阵就是非奇异矩阵.

方阵的逆矩阵的性质：

（i）若A可逆，则（A-1）-1=A；

（ii）若A可逆，数λ≠0，则λA可逆，且；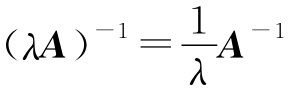

（iii）若A，B为同阶方阵，且A，B都可逆，则AB可逆，且

（AB）-1=B-1A-1；

（iv）若A可逆，则AT可逆，且（AT）-1=（A-1）T；

（v）若A可逆，则.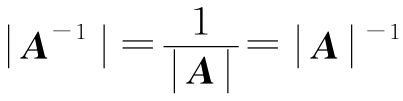

我们只证明性质（iii）、性质（iv），其他结论读者可以自行证明.

证　性质（iii）因为

（AB）（B-1A-1）=A（BB-1）A-1=AEA-1=AA-1=E，

所以

（AB）-1=B-1A-1.

性质（iv）因为

AT（A-1）T=（A-1A）T=ET=E，

所以

（AT）-1=（A-1）T.

性质（iii）可推广为：设A1，A2，…，An都是n阶可逆阵，则A1A2…An可逆，且

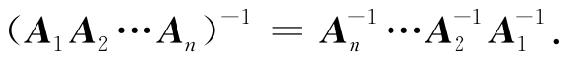
当|A|≠0时，还可定义

A0=E，A-k=（A-1）k，

其中，k为正整数. 这样，当|A|≠0，λ，μ为整数时，有

AλAμ=Aλ+μ，（Aλ）μ=Aλμ，

例2.8　设

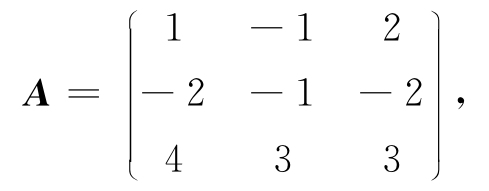
求A-1.

解　由

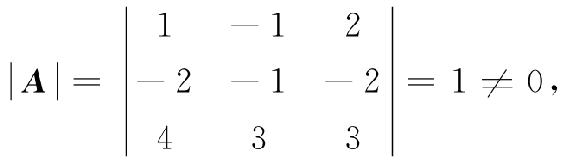
知A可逆. 且

解矩阵方程AXB=C.

解　因为|A|=1≠0，|B|=1≠0，所以A-1，B-1都存在，且

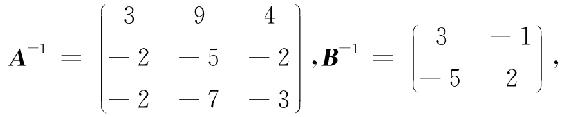
分别以A-1，B-1左乘与右乘矩阵方程的两边，得

A-1（AXB）B-1=A-1CB-1，

于是

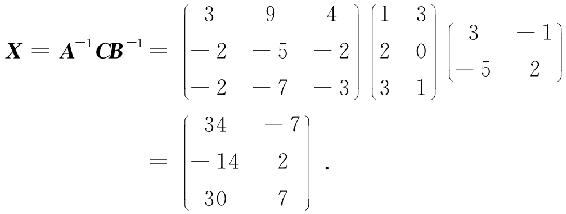
例2.10　已知方阵A满足

A2-A-4E=O，

试证A+E可逆，并求（A+E）-1

证　由A2-A-4E=O，得

（A+E）（A-2E）-2E=O，

即

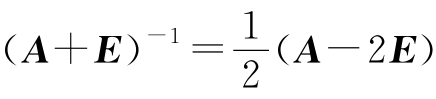
因此A+E可逆，且.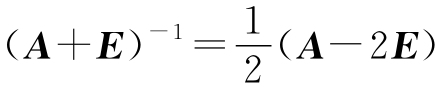

例2.11　设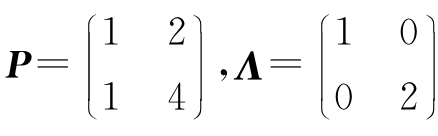，AP=PΛ，求An.

解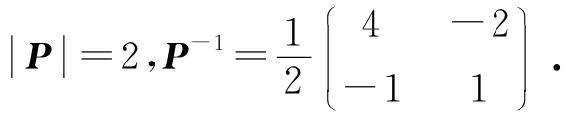　

A=PΛP-1，A2=PΛP-1PΛP-1=PΛ2P-1，…，An=PΛnP-1，

而易验证

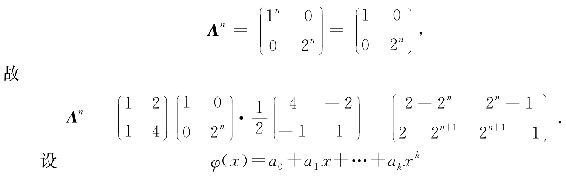
为x的k次多项式，A为n阶矩阵，记

φ（A）=a0E+a1A+…+akAk，

则φ（A）称为矩阵A的k次多项式.

我们常用例2.11计算An的方法来计算A的多项式φ（A）：

（i）若A=PAP-1，则An=PΛnP-1，从而

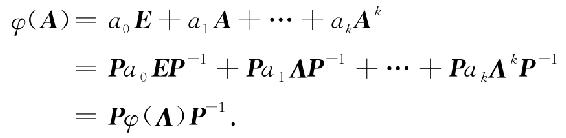
（ii）若A=diag（λ1，λ2，…λn）为对角矩阵，则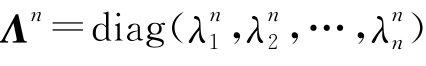，从而

φ（Λ）=a0E+a1Λ+…+akΛk