4.1 向量组及其线性组合

4.1　向量组及其线性组合

对二维和三维向量的概念进一步推广，我们现给出n维向量的定义.

定义1　n个有序的数a1，a2，…，an所组成的数组称为n维向量. 这n个数称为该向量的n个分量，第i个数ai称为第i个分量.

分量全为实数的向量称为实向量，分量为复数的向量称为复向量. 本书中若无特别说明，一般都指实向量. 分量全为0的向量称为零向量，记作0.

我们把n个分量写成一列

的形式，称为n维列向量. 同理，称

aT=（a1，a2，…an）

为n维行向量. 以后将n维行向量和n维列向量看成是两个不同的向量.

常用小写黑体字母。a，b，α，β等表示列向量，而用aT，bT，αT，βT等表示行向 量. 所讨论的向量在没有指明是行向量还是列向量时，就当成列向量. 由于行向量和列向量分别就是行矩阵和列矩阵，于是可利用矩阵的运算来进行向量间的运算.

若干个同维数的列向量（或同维数的行向量）所组成的集合称为向量组，常用大写字母表示. 例如一个m×n矩阵的全体列向量构成一个含n个m维列向量的向量组，它的全体行向量构成一个含m个n维行向量的向量组；又如线性方程组Am×nx=0（当R（A）<n时）的全体解向量构成一个含无穷多个n维列向量的向量组.（本章我们只讨论含有限个向量的向量组）

矩阵的列向量组和行向量组都是只含有限个向量的向量组；反之，一个含有限个向量的向量组总可以构成一个矩阵. 例如：

m个n维列向量所组成的向量组A:a1，a2，…，am构成一个n×m矩阵

A=（a1，a2，…，am）；

m个n维行向量所组成的向量组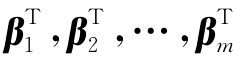构成一个m×n矩阵

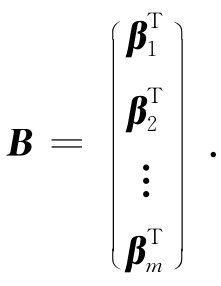
总之，含有限个向量的向量组可以与矩阵一一对应.

定义2　设有向量组A:a1，a2，…，am及任意给定的m个实数k1，k2，…，km，表达式

k1a1+k2a2+…+kmam

称为向量组A的一个线性组合，k1，k2，…，km，称为这个线性组合的系数.

若向量b等于向量组A的某一线性组合，即存在数λ1，λ2，…，λm，使

b=λ1a1+λ2a2+…+λmam，

则称向量b可由向量组A线性表示.

进一步可知，向量b可由向量组A线性表示，也就是方程组

x1a1+x2a2+…+xmam=b

有解. 由第3章定理4可得：

定理1　向量b可由向量组A:a1，a2，…，am线性表示的充分必要条件是矩阵A=（a1，a2，…，am）的秩等于矩阵B=（a1，a2，…，am，b）的秩.

定义3　若向量组B:b1，b2，…，bl的每个向量都可由向量组A:a1，a2，…，am线性表示，则称向量组B可由向量组A线性表示；若向量组A与向量组B可相互线性表示，则称向量组A与B等价.

把向量组A与B所构成的矩阵分别记为A=（a1，a2，…，am）和B=（b1，b2，…，bl），向量组B可由向量组A线性表示，即对每个向量bj（1，2，…，l）存在数k1j，k2j，…，kmj，使

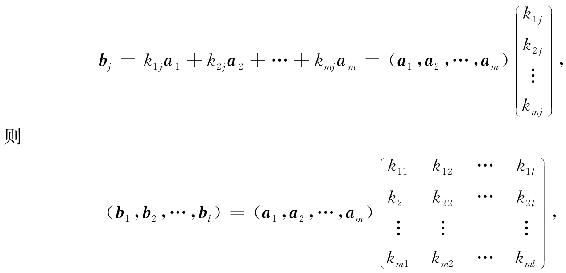
这里，矩阵Km×1=（kij）称为这一线性表示的系数矩阵.

由此可知，若Cm×n=Am×lBl×n，则矩阵C的列向量组可由A的列向量组线性表示，B为这一线性表示的系数矩阵，即

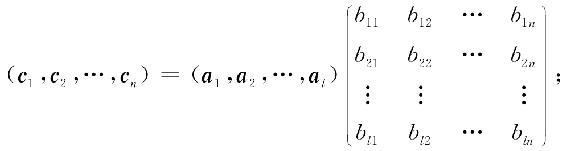
同理，C的行向量组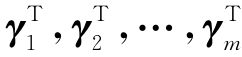可由B的行向量组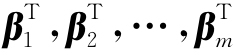线性表示，A为这一线性表示的系数矩阵，即

设矩阵A与B行等价，即矩阵A经初等行变换变成矩阵B，则B的每个行向量都是A的行向量的线性组合，即B的行向量组可由A的行向量组线性表示. 由于初等变换是可逆的，则矩阵B也可经初等行变换变成矩阵A，从而A的行向量组也可由B的行向量组线性表示. 于是A的行向量组与B的行向量组等价.

同理，若矩阵A与B列等价，则A的列向量组与B的列向量组等价.

向量组的线性组合、线性表示及等价的概念，可移用于线性方程组. 若方程组1与方程组2能相互线性表示，则称这两个方程组可以互推，可互推的方程组一定同解.

向量组B:b1，b2，…，bl可由向量组A:a1，a2.…，am线性表示，即存在系数矩阵Km×t，使

（b1，b2，…，bl）=（a1.a2，…am）K.

也就是矩阵方程

AX=B

有解，由第3章的定理5，即有

定理2　向量组B:b1，b2，…，bl可由向量组A:a1，a2，…am线性表示的充分必要条件是矩阵A＝（a1，a2，…，am）的秩等于矩阵（A，B）=（a1，…，am，b1，…bl）的秩，即

R（A）=R（A，B）.

推论　向量组A:a1，a2，…，am与向量组B:b1，b2，…，bl等价的充分必要条件是

R（A）=R（B）=R（A，B），

其中，A和B分别是向量组A和向量组B构成的矩阵.

证　由向量组A和向量组B可相互线性表示，根据定理2，它们等价的充要条件是

R（A）=R（A，B），且R（B）=R（B，A），

又因为R（A，B）=R（B，A），故充要条件是R（A）=R（B）=R（A，B）.

例4.1　设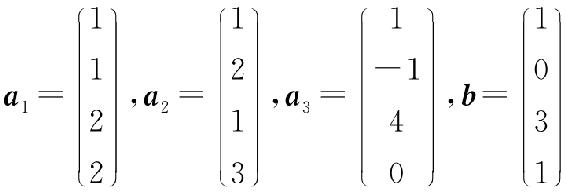，证明：向量b可由向量组a1，a2，a3线性表示，并写出其中一个线性表示式.

证　根据定理1，要证矩阵A=（a1，a2，a3）与矩阵B=（A，b）=（a1，a2，a3，b）的秩相等. 对B施行初等行变换：

可见，R（A）=R（B），所以向量b可由向量组a1，a2，a3线性表示.

由上述行最简形矩阵，可得方程组Ax=b的同解方程组为

x3为自由未知量，令x3=0，可得方程组的一个特解为

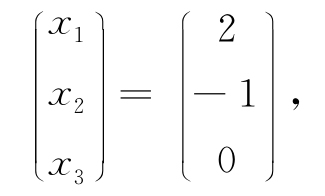
所以有

b=2a1-a2.

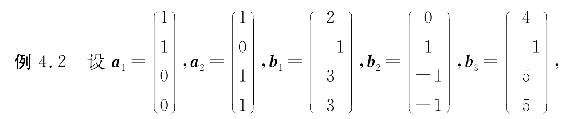
证明：向量组a1，a2与向量组b1，b2，b3等价.

证　记A=（a1，a2），B=（b1，b2，b3）. 根据定理2的推论，只需证

R（A）=R（B）=R（A，B）.

对矩阵（A，B）施行初等行变换：

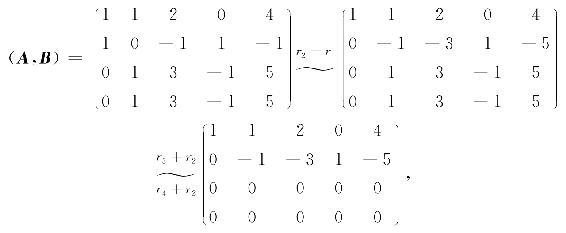
可见，R（A）=2，R（B）=2，R（A，B）=2，

因此

R（A）=R（B）=R（A，B），

故向量组a1，a2与向量组b1，b2，b3等价.

定理3　设A=（a1，a2，…，am），B=（b1，b2，…，bl），若向量组B：b1，b2，…，bl可由向量组A:a1，a2，….am线性表示，则R（B）≤R（A）.

证　依题意，由定理2有R（A）=R（A，B），而R（B）≤R（A，B），故

R（B）≤R（A）.