1.5 克莱姆（Cramer）法则

1.5　克莱姆（Cramer）法则

含有n个未知数x1，x2，…，xn的n个线性方程的方程组

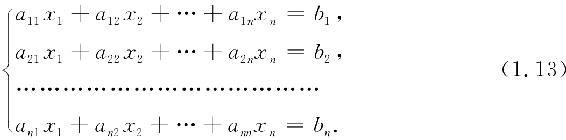
与二、三元线性方程组相类似，它的解可以用n阶行列式表示，即有下述的克莱姆（Cramer）法则.

定理5　若线性方程组（1.13）的系数行列式

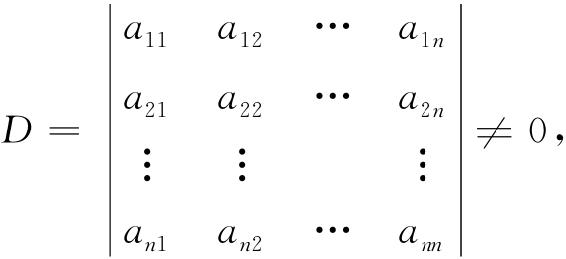
则方程组有唯一解，且可表示为

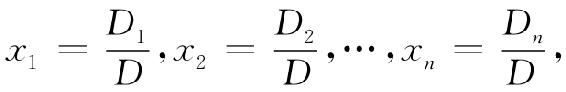
其中，Dj（j=1，2，…，n）是将D中的第j列元素换成方程组右端的常数项所得的行列式，即

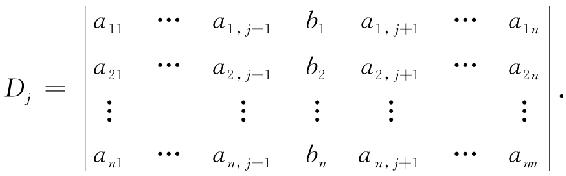
证　设x1，x2，…，xn是方程组（1.13）的解，按行列式的性质，有

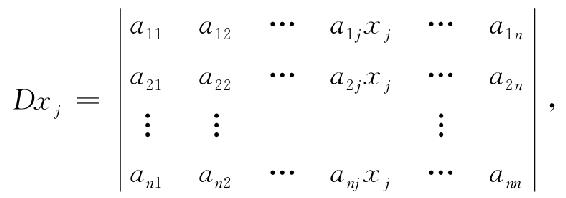
再把行列式的第1列，…，第j-1列，第j+1列，…，第n列分别乘以x1，…，xj-1，xj+1，…，xn加到第j列上去，行列式的值不变，即

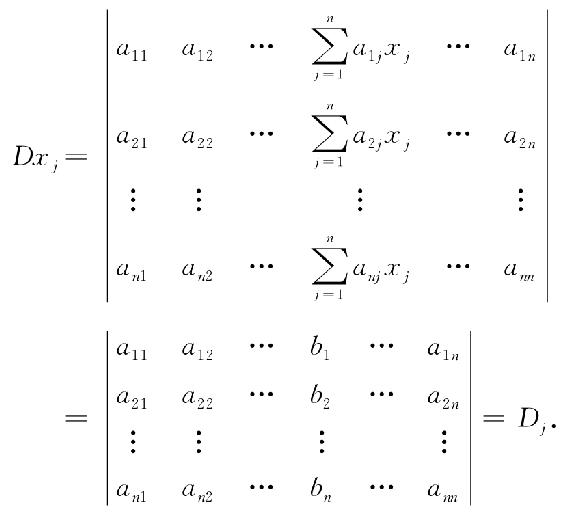
因D≠0，故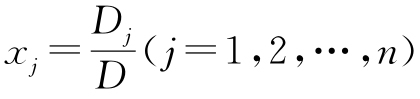为方程组的唯一解.

例1.14　求解线性方程组

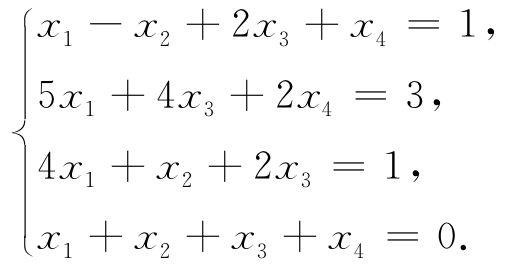
解　系数行列式为

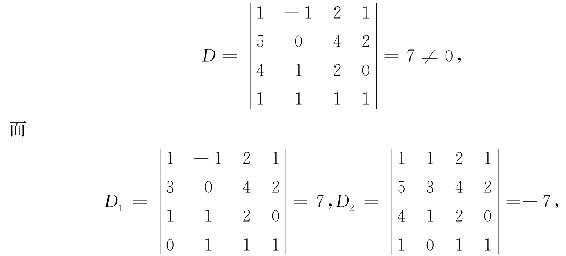
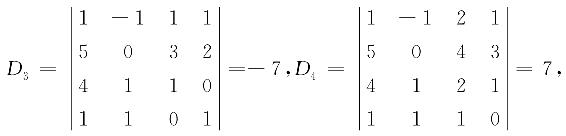
由克莱姆法则知，方程组有唯一解，为

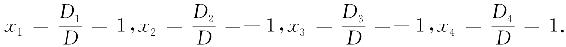
由此可见用克莱姆法则解方程组并不方便，因它需要计算很多行列式，故只适用于解未知量较少和某些特殊的方程组，但把方程组的解用一般公式表示出来，这在理论上是重要的.

使用克莱姆法则必须注意：

（i）未知量的个数与方程的个数要相等；

（ii）系数行列式不为零. 对于不符合这两个条件的方程组，将在以后的一般线性方程组中讨论.

常数项全为零的线性方程组

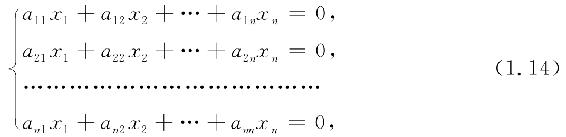
称为齐次线性方程组. 而方程组（1.13）称为非齐次线性方程组.

显然x1=x2=…=xn=0是方程组（1.14）的解，称为零解；若方程组（1.14）除了零解外，还有x1，x2，…，xn不全为零的解，称为非零解. 由克莱姆法则，可得以下定理：

定理6　如果齐次线性方程组（1.14）的系数行列式D≠0，则齐次线性方程组（1.14）只有零解.

定理6′　如果齐次线性方程组（1.14）有非零解，则它的系数行列式必为零.

定理6′　说明系数行列式D=0是齐次线性方程组有非零解的必要条件，在第3章中还将证明这个条件也是充分的.

例1.15　问λ取何值时，齐次线性方程组

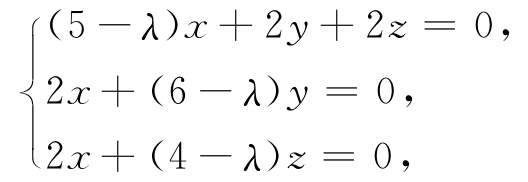
有非零解？

解　齐次线性方程组有非零解，则其系数行列式D=0，

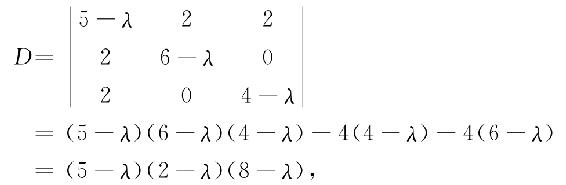
由D=0，得:λ=2，λ=5，λ=8.