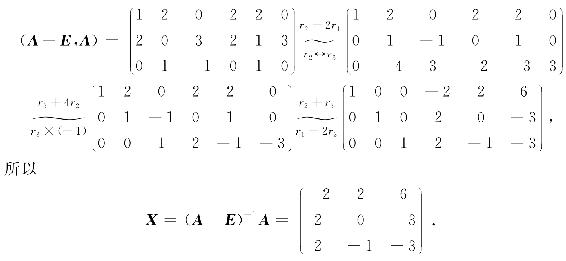3.2 初等矩阵

3.2　初等矩阵

定义2　由单位矩阵E经过一次初等变换得到的方阵称为初等矩阵.

3种初等变换对应3种形式的初等矩阵.

（1）对调单位矩阵的两行或两列

把单位矩阵E中的第i行和第1行对调（或第i列和第j列对调），得到初等矩阵

（2）用数k≠0乘单位矩阵的某行或某列

用数k≠0乘单位矩阵E中的第i行（或第i列），得到初等矩阵

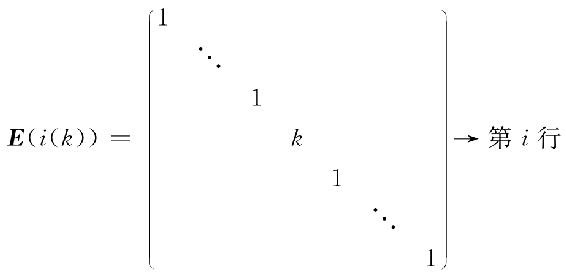
（3）把单位矩阵某行（列）的k倍加到另一行（列）上去

把单位矩阵E中的第7行的k倍加到第i行上（或第i列的k倍加到第j列上），得到初等矩阵

定理1　设A是一个m×n矩阵，则对A施行一次初等行变换，相当于用相应的m阶初等矩阵左乘A；对A施行一次初等列变换，相当于用相应的n阶初等矩阵右乘A.（此定理请读者自行证明）

由于矩阵的初等变换可逆，而初等变换对应初等矩阵，且初等变换的逆变换仍然是同类型初等变换，容易验证初等矩阵可逆，且初等矩阵的逆矩阵是对应初等变换的逆变换所对应的初等矩阵，即

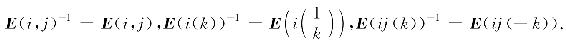
定理2　方阵A可逆的充分必要条件是存在有限个初等矩阵P1，P2，…，Ps，使A=P1P2…Ps.

证　先证充分性.

设A=P1P2…Ps，因为初等矩阵可逆，且有限个可逆矩阵的乘积仍可逆，故A可逆.

再证必要性.

设n阶方阵A可逆，A的标准形为F，由于A～F，所以F经过有限次初等变换可化为A，即存在有限个初等矩阵P1，P2，…，Ps使得

A=P1…PlFPl+1…Ps，

因为A可逆，P1，P2，…，Ps也可逆，故F可逆. 假设

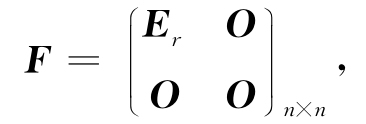
则r=n，否则|F|=0，与F可逆矛盾，即F=E.从而

A=P1…PlFPl+1…Ps=P1…PlEPl+1…Ps=P1P2Ps.

从上述证明中可得到，可逆矩阵的标准形是单位矩阵. 把定理2的结果改写成

A=P1P2…PsE，或A=EP1P2…Ps，

再结合定理1可得到以下推论.

推论1　方阵A可逆的充分必要条件是.

推论2　m×n矩阵A与B等价的充分必要条件是存在m阶可逆矩阵P及n阶可逆矩阵Q使得B-PAQ.

以上两推论请读者自行证明.

推论3　对于方阵A，若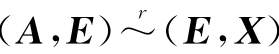，则A可逆，且A-1=X.

证　因为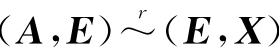，由定理1可知，存在初等矩阵P1，P2，…，Ps，使得

Ps…P2P1A=E，Ps…P2P1E=X.

由于P1，P2，…，Ps可逆，所以A可逆. 在Ps…P2P1A=E两边右乘A-1得到

Ps…P2P1AA-1=EA-1=A-1，

即

A-1=Ps…P2P1=X.

由推论3可知，3.1节例3.1中A可逆，且

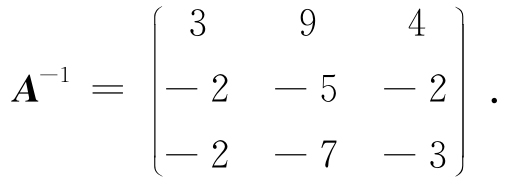
推论4　对于n阶矩阵A与n×s矩阵B，若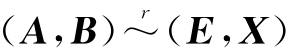，则A可逆，且X=A-1B.特别地，对于n个未知数n个方程的线性方程组Ax=b，若增广矩阵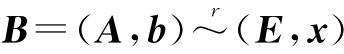，则A可逆，且x=A-1b为方程组的唯一解.

推论4的证明与推论3类似，请读者自行证明.

例3.2　设

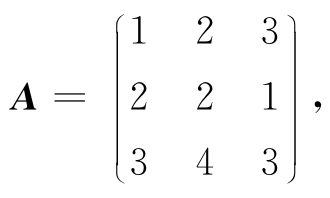
求A-1.

解

例3.3　求解矩阵方程AX=B，其中

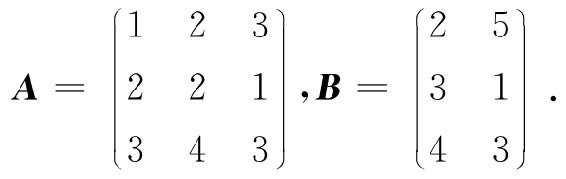
解　若A可逆，则X=A-1B.

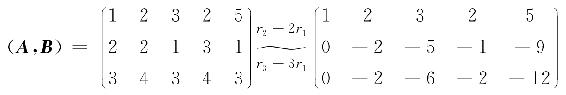
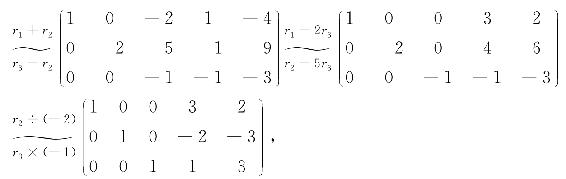
由推论4知，A可逆，且.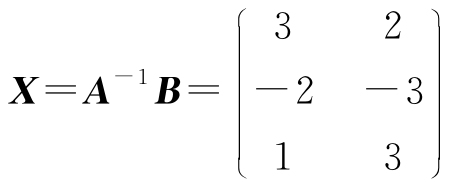

当然，也可先求出A-1，再通过矩阵的乘法求出X=A-1B.

例3.4　求解矩阵方程AX=X+A，其中

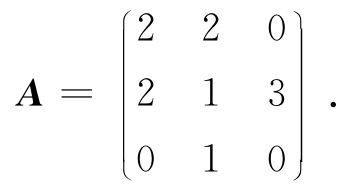
解　矩阵方程变形为（A-E）X=A，而|A-E|=1≠0，所以A-E可逆.