习题3

习题3

1. 把下列矩阵化为行最简形矩阵：

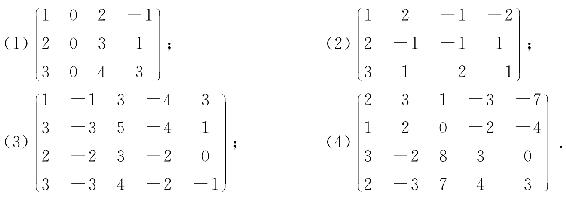
2. 利用矩阵的初等变换求下列矩阵的逆矩阵：

3. 利用矩阵的初等变换求解下列矩阵方程：

4. 求下列矩阵的秩，并求其一个最高阶非零子式：

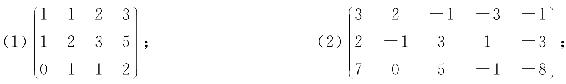
5. 设A，B都是m×n矩阵，证明A～B的充分必要条件是R（A）=R（B）.

6. 设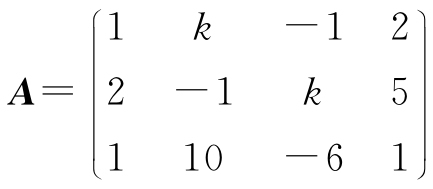，讨论矩阵A的秩.

7. 求解下列齐次线性方程组：

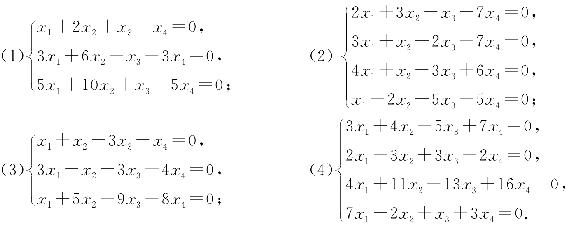
8. 求解下列非齐次线性方程组：

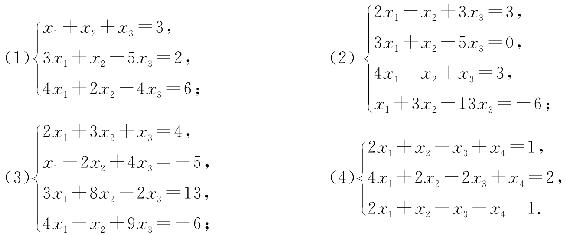
9. 非齐次线性方程组

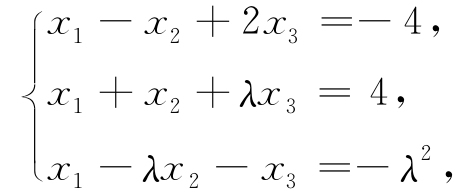
当λ取何值时，此方程组无解、有唯一解、有无穷多解？

10. 非齐次线性方程组

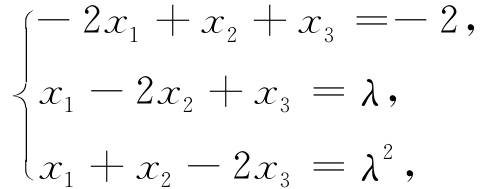
当λ取何值时有解？并求出它的通解.

11. λ取何值时，非齐次线性方程组

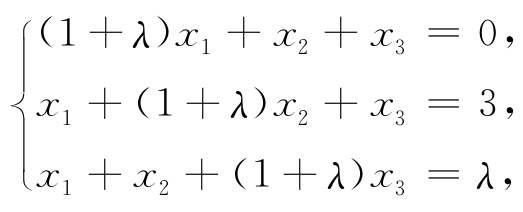
（1）有唯一解：（2）无解；（3）有无穷多解，并在此情形下求出其通解.

12. 证明R（A）=1的充分必要条件是存在非零列向量a及非零行向量bT，使A=abT.

13. 设A为m×n矩阵，证明：

（1）方程AX=Em有解的充分必要条件是R（A）=m;

（2）方程YA=En有解的充分必要条件是R（A）=n.

14. 设A为m×n矩阵，证明：若AX=AY，且R（A）=n，则X=Y.