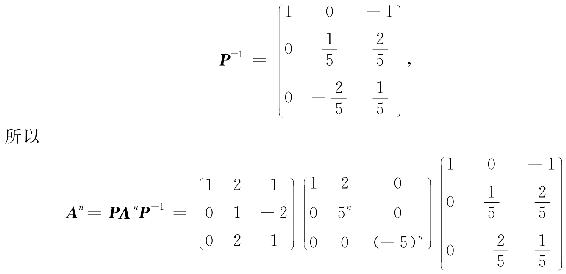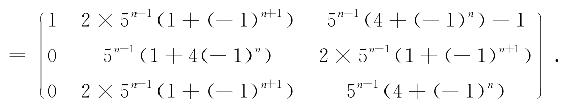5.3 相似矩阵

5.3　相似矩阵

5.3.1　相似矩阵定义

定义8　设A，B都是n阶方阵，若存在一个n阶可逆矩阵P，使

P-1AP=B，

则称A与B是相似的，或称B是A的相似矩阵. 称P-1AP为对A作相似变换，可逆矩阵P称为把A变成B的相似变换矩阵.

矩阵的相似关系是一种等价关系，即有

（i）反身性　A与A相似；

（ii）对称性　若A与B相似，则B与A相似；

（iii）传递性　若A与B相似，B与C相似，则A与C相似.

相似矩阵还具有如下性质：

性质1　若A与B相似，则R（A）=R（B），且|A|=|B|.

证　若A与B相似，则存在可逆矩阵P，使P-1AP=B，则A与B等价，因而R（A）=R（B），且

|B|＝|P-1AP|=|P-1||A||P|=|A|.

性质2　若A可逆，且A与B相似，则B可逆，且A-1与B-1也相似.

证　若A与B相似，则A与B等价，又A可逆，故B可逆. 由

P-1AP=B，

得

（P-1Ap）-1=B-1，

即P-1A-1P=B-1，所以A-1与B-1相似.

性质3　若A与B相似，则Ak与Bk（k为整数）相似.

证　若A与B相似，则由P-1AP=B，

得

（P-1AP）k=Bk，

而

（P-1AP）k=（P-1AP）（P-1AP）…（P-1AP）=P-1AkP，

所以Ak与Bk相似.

定理3　若n阶方阵A与B相似，则A与B的特征多项式相同，从而A与B的特征值也相同.

证　设A与B相似，所以存在可逆矩阵P，使得P-1AP=B，则

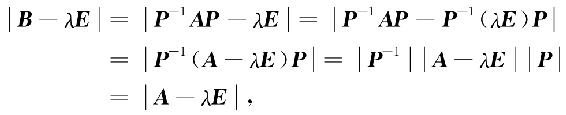
即A与B具有相同的特征多项式，从而也具有相同的特征值.

说明：定理3的逆命题并不成立，即特征多项式相同的矩阵不一定相似. 例如

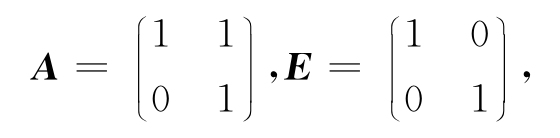
A与E的特征多项式相同，但A与E不相似，因为单位矩阵只能与自身相似.

推论　若n阶方阵A与对角矩阵

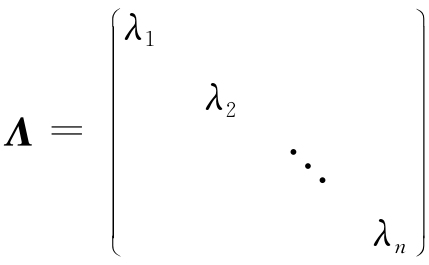
相似，则λ1，λ2，…，λn是A的n个特征值.

证　易知λ1，λ2，…，λn是A的n个特征值，由定理3知λ1，λ2，…，λn也是A的n个特征值.

5.3.2　矩阵的对角化

在矩阵中，对角矩阵是一种比较简单的矩阵，它的许多性质及运算相对来说都比较明显和简便. 如果一个矩阵能够相似于一个对角矩阵，那么就说它可以对角化. 利用矩阵的对角化可以把复杂矩阵转化为简单的对角矩阵进行研究.

下面讨论的主要问题是：对n阶方阵A，在什么条件下能与一个对角矩阵相似？其相似变换矩阵P具有什么样的结构？

定理4　n阶方阵A与对角矩阵相似的充分必要条件是A有n个线性无关的特征向量.

证　先证必要性. 设n阶方阵A与对角矩阵A相似，记

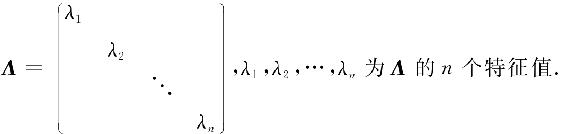
由P-1AP=A，得AP=PA，

将P按列分块，记P=（p1，p2，…，pn），则上式写为

A（p1，p2，…，pn）=（λ1p1，λ2p2，…，λnpn），

于是，

Ap1=λ1p1，Ap2=λ2p2，...，Apn=λnpn，

则λ1，λ2，…，λn为A的特征值，p1，p2，…，pn为A的分别属于特征值λ1，λ2，…λn的特征向量，由于P可逆，所以p1，p2，…，pn线性无关.

再证充分性. 若A有n个线性无关的特征向量p1，p2，…，pn，假设它们对应的特征值分别为λ1，λ2，…，λn，则

Api=λipi（i=1，2，…，n），

即有

A（p1，p2，…，pn）=（Ap1，Ap2，…，Apn）=（λ1p1，λ2p2，…，λnpn）

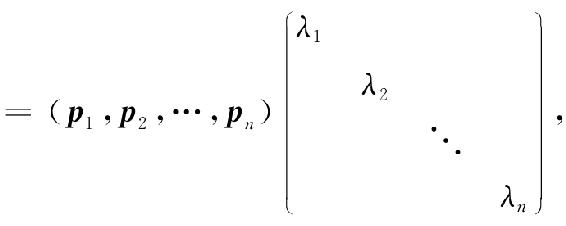
因为p1，p2，…，pn线性无关，则p=（p1，p2，…，pn）为可逆矩阵，从而

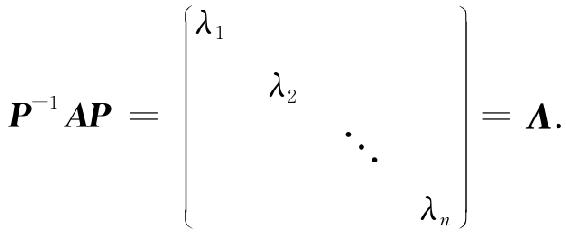
在5.2节例5.4、例5.5、例5.6中，我们发现例5.4、例5.5中的矩阵可以对角化，而例5.6中三阶方阵A最多只能找到两个线性无关的特征向量，所以不能对角化.

由5.2节的性质5，可得如下推论：

推论　若n阶方阵A有n个互不相同的特征值，则A与对角矩阵相似.

再比较例5.5和例5.6，发现例5.6不能对角化的原因是其特征值中二重根1对应的齐次线性方程组（A-E）x=0的基础解系中只有一个线性无关的解向量，而例5.5的特征值中的二重根2对应的齐次线性方程组（A-2E）x=0的基础解系中，却有两个线性无关的解向量. 由此，可得如下定理：

定理5　若对于n阶方阵A的任一k重特征值λ，有R（A-λE）=n-k，则A可对角化.

证　对A的任一k重特征值，R（A-λE）=n-k，则齐次线性方程组（A-λE）x=0的基础解系中解向量的个数为k，则必对应k个线性无关的特征向量，则A必有n个线性无关的特征向量，故A可对角化.

例5.9　设矩阵A与B相似，其中

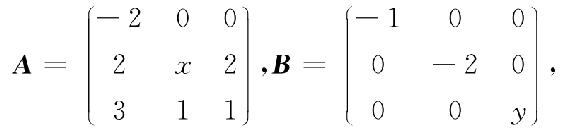
求x与y的值.

解　A的特征多项式为

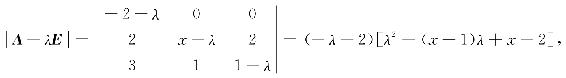
显然，B的特征值为-1，-2，y，由于A与B相似，所以-1，-2，y也A的特征值，将λ＝-1代入A的特征方程得x=0，则A的特征多项式为

（-λ-2）（λ2-λ-2），

则A的特征值为-1，-2，2，所以y=2.

例5.10　设方阵

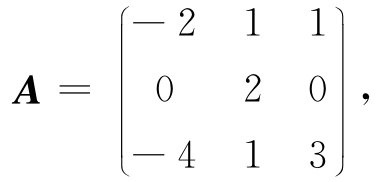
问A是否可对角化？若能对角化，找一可逆矩阵P，使P-1AP为对角矩阵.

解　A的特征多项式为

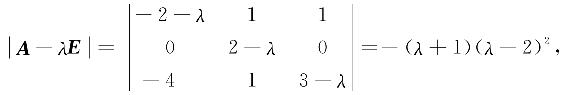
所以A的特征值为λ1＝-1，λ2=λ3=2.

当λ1＝-1时，解齐次线性方程组（A+E）x=0，由

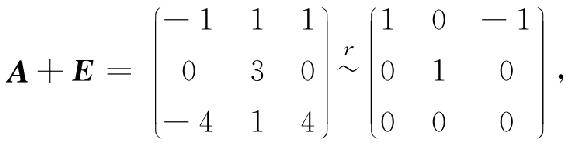
得基础解系为

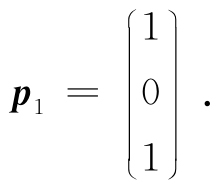
当λ2=λ3=2时，解齐次线性方程组（A-2E）x=0，由

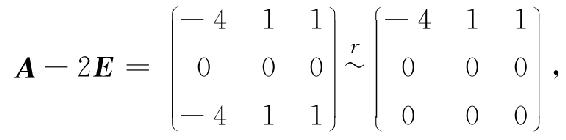
得基础解系为

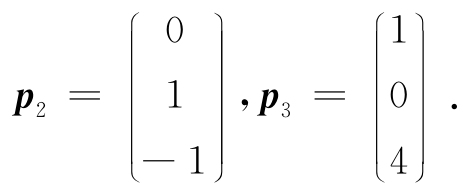
因为p1，p2，p3线性无关，即A有3个线性无关的特征向量，故A可对角化.

令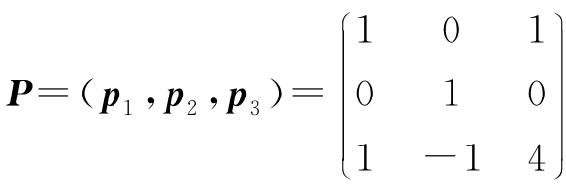，则P为可逆矩阵，且有

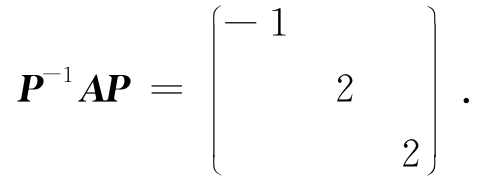
例5.11　设方阵

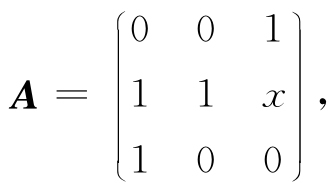
问x为何值时，A可对角化.

解　A的特征多项式为

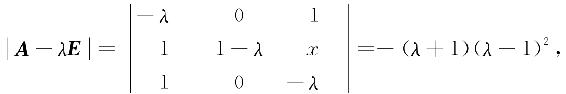
所以A的特征值为λ1＝-1，λ2=λ3=1.

对应单根λ1＝-1，可求得线性无关的特征向量恰有1个，现要使A可对角化，则二重根，λ2=λ3=1要有两个线性无关的特征向量，即线性方程组（A-E）x=0的基础解系中有两个解向量，亦即R（A-E）=1.

要使R（A-E）=1，则x＝-1.

所以，当x＝-1时，A可对角化.

例5.12　设方阵

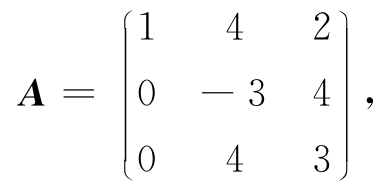
求An（n∈N）.

解　A的特征多项式为

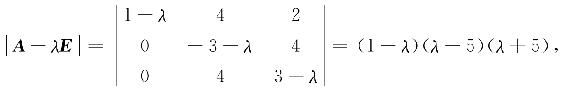
所以A的特征值为λ1=1，λ2=5，λ3＝-5，它们对应的特征向量分别为

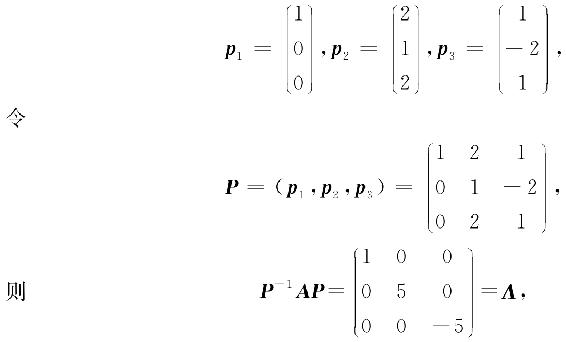
所以A=PAP-1，

可求得