4.5 向量空间

4.5　向量空间

4.5.1　向量空间的概念

定义7　设V是非空的n维向量的集合，若集合V对向量的加法及向量的数乘这两种运算封闭，则称集合V是一个向量空间.

所谓对运算“封闭”是指，对任何a∈V，b∈V，有a+b∈V；对任何a∈V，λ∈R，有λa∈V.

例4.11　所有n维向量的全体所组成的集合Rn是一个向量空间，它是R2和R3的推广.

例4.12　集合V1=｛（0，x2，…，xn）|x2，…，xn∈R｝是一个向量空间. 因为对任意a=（0，x2，…，xn），b=（0，y2，…，yn）∈V1，有a+b=（0，x2+y2，…，xn+yn）∈V1；对数λ∈R，有λa=（0，λx2，…，λxn）∈V1.

例4.13　集合V2=｛（1，x2，…，xn）|x2，…，xn∈R｝不是向量空间. 因为对任意a=（1，x2，…，xn）∈V2，而.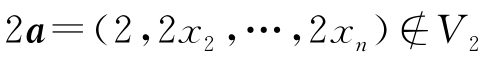

例4.14　齐次线性方程组的解集S=｛x|Ax=0｝是一个向量空间（称为齐次线性方程组的解空间）. 因为由齐次线性方程组的解的性质可知其解集S对向量的线性运算封闭.

例4.15　非齐次线性方程组的解集S=｛x|Ax=b｝不是向量空间. 因为当S为空集时，S不是向量空间：当S非空时，若η∈S，则A（2η）=2b≠b，知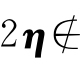S.

定义8　设a.b是两个已知的n维向量，则它们的一切线性组合构成的集合

V=｛x=λa+μb|λ，μ∈R｝

是一个向量空间，称为向量a，b的生成空间，记作L（a，b）.

事实上，对任意的x1∈V及x2∈V，存在λ1，λ2，μ1，μ2∈R，使得

X1=λla+μ1b，

x2=λ2a+μ2b，

于是

x1+x2=（λl+λ2）a+（λ1+μ2）b∈V，

并对任意λ∈R有

λx1=λ（λ1a+μ1b）=（λλ1）a+（λμ1）b∈V，

这表明集合V对线性运算封闭，因此V是一个向量空间.

一般地，向量组a1，a2，…，am的生成空间为

V=｛（x=λ1a1+λ2a2+…+λmam|λ1，λ2，…，λm∈R），

记作L（a1，a2，…，am）.

例4.16　证明等价向量组生成的向量空间相等.

证　设向量组a1，a2，…，am与向量组b1，b2，…，bl等价，记

L1=L（a1，a2，…，am）=｛x=λ1a1+λ2a2+…+λmam｜λ1.λ2，…，λm∈R｝，

L2=L（b1，b2，…，bl）=｛x=μ1b1+μ2b2+…+μlb1|μl，μ2，…，μl∈R｝，

要证明L1=L2.

设x∈L1，则x可由a1，a2，…，am线性表示，又因a1，a2，…，am可由b1，b2，…，bl线性表示，故x可由b1，b2，….bl线性表示，所以.

同理可证：.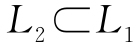

因为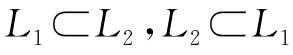，所以L1=L2.

定义9　设有向量空间V1、V2，若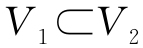，则称V1是V2的子空间.

例如任何由n维向量所组成的向量空间V，总有，所以这样的向量空间总是Rn的子空间.

4.5.2　向量空间的基与维数

定义10　设向量a1，a2，…，ar是向量空间V中的r个向量，且满足：

（i）a1，a2，…，ar线性无关；

（ii）V中的任一向量都可由a1，a2，…，ar线性表示：则称a1，a2，…，ar为向量空间V的一个基，r称为向量空间V的维数，并称V是r维向量空间.

只含零向量的集合也是一个向量空间，它没有基，它的维数规定为0.

若把向量空间V看成向量组，则V的基就是向量组的最大无关组，V的维数就是向量组的秩.

任何n个线性无关的n维向量都可以是Rn的一个基，由此可知Rn的维数为n.

定义11　设向量a1，a2，…，ar是向量空间V的一个基，a∈V，若

a=x1a1+x2a2+…+xrar，

则称有序数组x1，x2，…，xr为向量a在基al，a2，…，ar下的坐标，记作（x1，x2，…，xr）T.

特别地，在n维向量空间Rn中取单位坐标向量组e1，e2，…，en为基，则以x1，x2，…，xn，为分量的向量x，可以表示为

x=x1e1+x2e2+…+xnen

可见向量在基e1，e2，…，en中的坐标就是该向量的分量.e1，e2，…，en。称为Rn的自然基.

例4.17　设

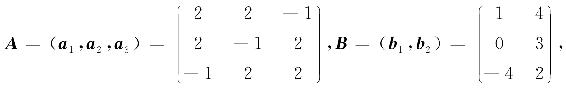
验证a1，a2，a3是R3的一个基，并求b1，b2在这个基中的坐标.

解　要证a1，a2，a3是R3的一个基，只要证a1，a2，a3。线性无关，即证A～E.

设b1=x11a1+x21a2+x31a3，b2=x12a1+x22a2+x32a3，即

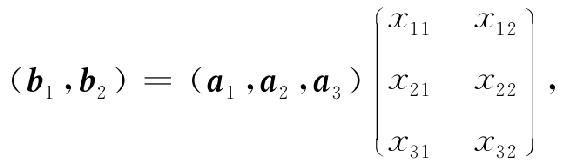
记为B=AX，对矩阵（A，B）进行初等行变换，若A能变为E，则a1，a2，a3。就是R3的一个基，且当A变为E时，B变为X=A-1B.

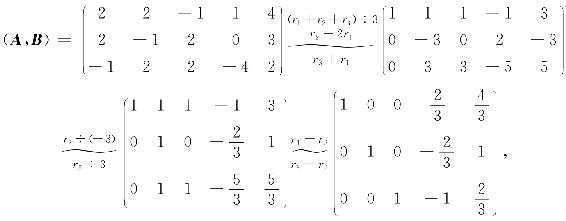
可见A～E，故a1，a2，a3是R3的一个基，且

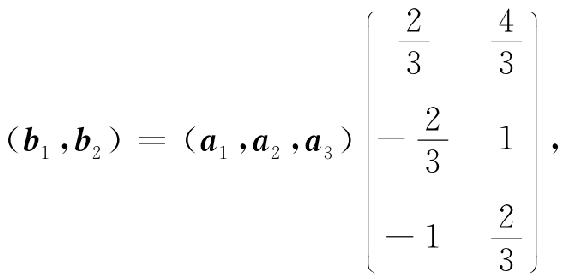
即b1，b2在基a1，a2，a3中的坐标依次为