3.3 矩阵的秩
3.3 矩阵的秩
在3.1节中我们指出,给定一个m×n矩阵A,它的标准形
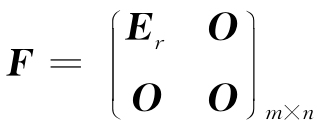
由数r完全确定. 这个数也就是A的行阶梯形矩阵中非零行的行数,这个数便是矩阵A的秩. 但由于这个数的唯一性尚未说明,因此,我们用另一种方式来给出矩阵的秩的定义.
3.3.1 矩阵的秩的定义
定义3 在m×n矩阵A中,任取k行k列(k≤min{m,n}),位于这些行列交叉处的k2个元素按原来的次序所构成的k阶行列式,称为A的k阶子式.
由排列组合知识可知,矩阵Am×n共有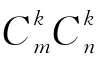 个k阶子式.
个k阶子式.
例如
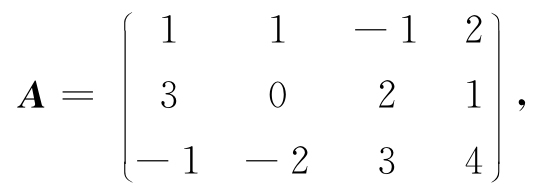
从A中选取第1、第2行及第2、第4列,它们交叉处元素构成A的一个二阶子式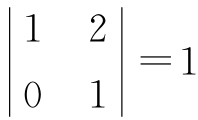 . 再如取A的第1、第2、第3行及第1、第3、第4列对应的A的三阶子式为
. 再如取A的第1、第2、第3行及第1、第3、第4列对应的A的三阶子式为
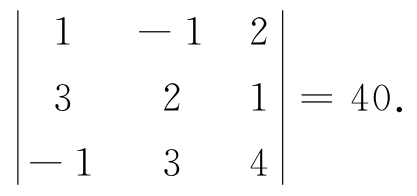
显然A的每一元素aij都是A的一阶子式,当A为n阶方阵时,其n阶子式为|A|.
定义4 设在m×n矩阵A中有一个不等于0的r阶子式D,且所有的r+1阶子式(如果存在的话)全等于0,则D称为矩阵A的最高阶非零子式. 数r称为矩阵A的秩,记作R(A)=r.我们规定零矩阵的秩为0.
注意:
(i)由行列式的展开法则可知,在A中,当所有r+l阶子式全等于0时,所有高于r+l阶的子式也全等于0,因此把r阶非零子式称为A的最高阶非零子式,而A的秩R(A)就是A中不等于0的子式的最高阶数.
(ii)若矩阵A中存在某个s阶子式不等于0,则R(A)≥s;若所有t阶子式全为0,则R(A)<t.
(iii)对任意m×n矩阵A,有O≤R(A)≤min{m,n}.
(iv)对任意m×n矩阵A,有R(A)=R(AT).
(v)对n阶方阵A,若|A|≠0,则R(A)=n,此时方阵A可逆,所以可逆矩阵又称满秩矩阵;若|A|=0,则R(A)<n,此时方阵A不可逆,因此不可逆矩阵又称降秩矩阵(或奇异矩阵).
例3.5 求下列矩阵的秩:
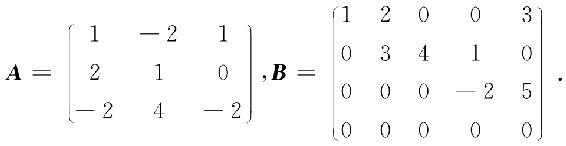
解 易看出,A中有一个二阶子式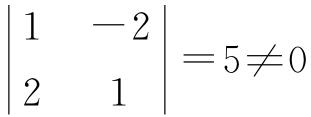 ,而A的三阶子式只有一个,且|A|=0,所以R(A)=2.
,而A的三阶子式只有一个,且|A|=0,所以R(A)=2.
B是一个行阶梯形矩阵,其非零行的行数为3,因此B的所有4阶子式全为0. 而以3个非零行的第一个非零元为对角线的三阶子式

是一个上三角行列式,它显然不等于0,因此,R(B)=3.
3.3.2 矩阵的秩与矩阵的初等变换
对于一般的矩阵,当行数与列数较高时,按定义求矩阵的秩是非常麻烦的. 由例3.5可以看出,当矩阵是行阶梯形矩阵时,它的秩就等于非零行的行数,一看便知. 因此,我们自然想到用矩阵的初等变换把矩阵化为行阶梯形矩阵,但进行初等变换后,矩阵的秩是否会发生变化呢?
定理3 若A~B,则R(A)=R(B).
证 先证明A经过一次初等行变换变为B,则R(A)≤R(B).
设R(A)=r,则A中必存在某个r阶子式D≠0. 下面对3种初等行变换分别证明R(A)≤R(B).
(1)当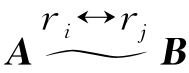 时,在B中取与D有相同序号的行和列所组成的子式D1,则D1与D完全相同,或D1是D交换两行得到的,故有
时,在B中取与D有相同序号的行和列所组成的子式D1,则D1与D完全相同,或D1是D交换两行得到的,故有
D1=D,或D1=-D,
即D1≠0,故R(B)≥r=R(A);
(2)当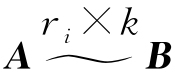 (常数k≠0)时,在B中取与D有相同序号的行和列所组成的子式D2,此时
(常数k≠0)时,在B中取与D有相同序号的行和列所组成的子式D2,此时
D2=D,或D2=kD,
即D2≠0,故R(B)≥r=R(A);
(3)当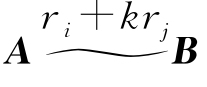 时,由于对变换ri↔rj,结论成立,因此只需考虑
时,由于对变换ri↔rj,结论成立,因此只需考虑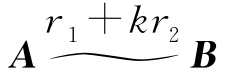 这一特殊情况分3种情形:
这一特殊情况分3种情形:
①A的r阶子式D不包含A的第1行,这时D也是B的r阶非零子式,故R(B)≥r=R(A);
②D包含A的第1行也包含A的第2行时,在B中取与D有相同序号的行和列所组成的子式D3,由行列式的性质知D3=D≠O,故R(B)≥r=R(A);
③D包含A的第1行但不包含A的第2行时,在B中取与D有相同序号的行和列所组成的子式D4,记作
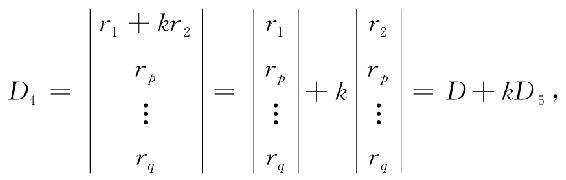
其中,D5也是B的r阶子式,由D4-kD5=D≠O可知,D4与D5不同时为0,所以B中总存在r阶非零子式D4或D5,故R(B)≥r=R(A).
以上证明了A经一次初等行变换变为B,有R(A)≤R(B). 由于B也可经一次初等行变换变为A,故有R(B)≤R(A). 因此R(A)=R(B).
经一次初等行变换矩阵的秩不变,即可知经有限次初等行变换矩阵的秩也不变.
设A经初等列变换变为B,则AT经初等行变换变为BT,由上面的证明可知R(AT)=R(BT),又R(A)=R(AT),R(BT)=R(BT),因此R(A)=R(B).
综上所述,若A经有限次初等变换变为B(即A~B),则R(A)=R(B).
由定理3可知,要求矩阵的秩,只要把矩阵用初等行变换化为行阶梯形矩阵,则行阶梯形矩阵中,非零行的行数即为该矩阵的秩.
例3.6 设
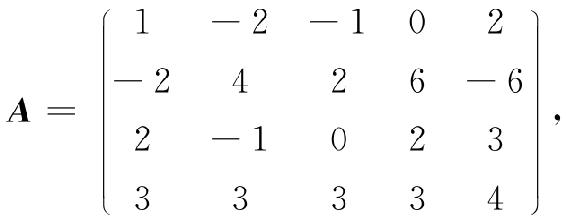
求矩阵A的秩,并求A的一个最高阶非零子式.
解
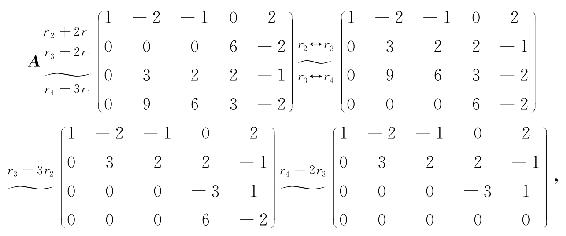
因为行阶梯形矩阵中,有3个非零行,所以R(A)=3.
记A=(a1,a2,a3,a4,a5),则矩阵A0=(a1,a2,a4)的行阶梯形矩阵为

可知R(A0)=3,故A0中必存在一个3阶非零子式,它也是A的一个3阶非零子式. 现计算A0的前3行构成的子式.
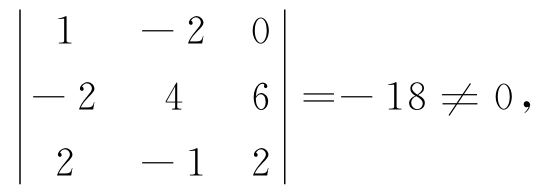
因此这个子式就是A的一个最高阶非零子式.
例3.7 设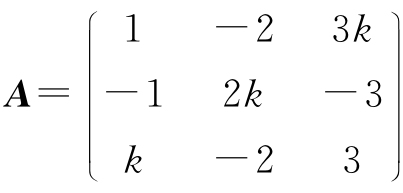 ,问k为何值时,可使
,问k为何值时,可使
(1)R(A)=1;(2)R(A)=2;(3)R(A)=3?
解
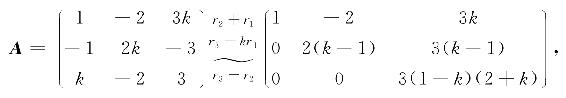
因此
(1)当k=1时,R(A)=1;
(2)当k=-2时,R(A)=2;
(3)当k≠1且k≠-2时,R(A)=3.
3.3.3 矩阵的秩的性质
前面已经提出了矩阵的秩的一些基本性质,将这些性质归纳起来,阐述如下:
性质1 0≤R(Am×n)≤min{m,n},且R(A)=0的充分必要条件是A=O.
性质2 R(A)=R(AT).
性质3 R(A)=R(kA)(k≠0).
性质4 若A~B,则R(A)=R(B).
性质5 若P,Q可逆,则R(PAQ)=R(A).
性质6 max{R(A),R(B)}≤R(A,B)≤R(A)+R(B),特别地,当B=b为列向量时,有
R(A)≤R(A,b)≤R(A)+1.
证 因为A的子式和B的子式都是(A,B)的子式,所以R(A)≤R(A,B),R(B)≤R(A,B),因此max{R(A),R(B)}≤R(A,B).
设R(A)=s,R(B)=t.把A和B分别作列变换化为列阶梯形矩阵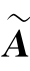 和
和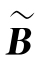 ,则
,则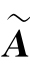 和
和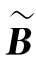 中分别含有s个和t个非零列,可设
中分别含有s个和t个非零列,可设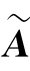 ,
,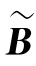 分别为
分别为
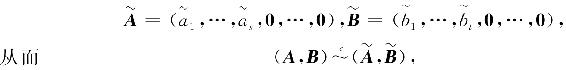
由于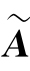 ,
,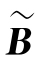 中只含有s+t个非零列,因此R(
中只含有s+t个非零列,因此R(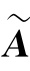 ,
,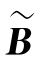 )≤s+t,而R(A,B)=R(
)≤s+t,而R(A,B)=R(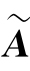 ,
,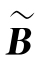 ),故R(A,B)≤s+t,即
),故R(A,B)≤s+t,即
R(A,B)≤R(A)+R(B).
性质7 R(A±B)≤R(A)+R(B).
证 对矩阵(A±B,B)作初等列变换,易知
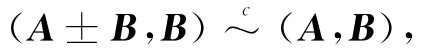
于是
R(A±B)≤R(A±B,B)=R(A,B)≤R(A)+R(B).
性质8 R(AB)≤min{R(A),R(B)}.(证明见3.4节)
性质9 若Am×nBn×l=O,则R(A)+R(B)≤n.(证明见第4章)
例3.8 设A为n阶方阵,证明R(A+E)+R(A-E)≥n.
证 因为(A+E)+(E-A)=2E,由性质7有,
R(A+E)+R(E-A)≥R(2E)=n,
而R(E-A)=R(A-E),故
R(A+E)+R(A-E)≥n.
