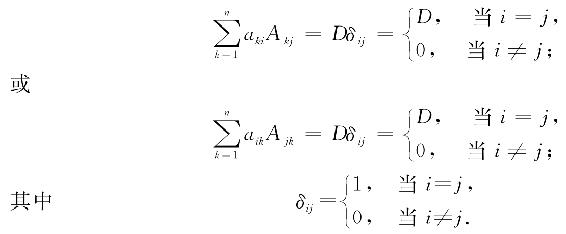1.4 行列式按行（列）展开

1.4　行列式按行（列）展开

一般说来，行列式的阶数越低，计算就越简单. 因此，我们自然会考虑是否能用低阶行列式来表示高阶行列式的问题. 为此，我们需要先引入余子式和代数余子式的概念.

定义2　在n阶行列式中，把元素aij所在的第i行和第j列划去，余下的n-1阶行列式（依原来的排法），称为元素aij的余子式，记作Mij；记

Aij=（-1）i+jMij，

称Aij为元素aij的代数余子式.

例如四阶行列式

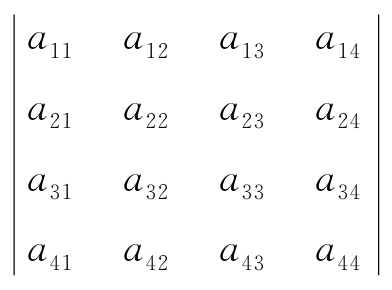
中，元素a23的余子式和代数余子式分别为

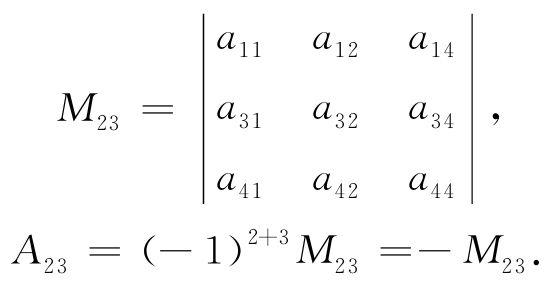
引理　一个n阶行列式D，若第i行所有元素除aij外全为零，则该行列式等于aij与它的代数余子式的乘积，即

D=aijAij.

证　先证aij位于第1行第1列的情形，此时

这是1.3节例1.11中当k=1时的特殊情形，按1.3节例1.11的结论有

D=a11M11=a11A11.

再证一般情形，此时

将D的第i行依次与第i-1行，第i-2行，…，第1行对调，这样，元素aij就调到了第1行第j列的位置，调换次数为i-1次：再把第j列依次与第j-1列，第j-2列，…，第1列对调，元素aij最终调到了第1行第1列的位置，调换次数为j-1次，总共经过i+j-2次对调，将元素aij调到第1行第1列的位置. 第1行其他元素为零，所得的行列式记作D1，则

D1=（-1）i+j-2D=（-1）i+jD，

而aij在D1中的余子式仍然是aij在D中的余子式Mij.利用前面的结果，有

D1=aijMij，

于是

D=（-1）i+jD1=（-1）i+jaijMij=aijAij.

定理4　行列式等于它的任一行（列）的各元素与其对应的代数余子式的乘积之和，即

D=ailAil+ai2Ai2+…+ainAin（i=1，2，…，n），

或

D=a1jA1j+a2jA2j＋…＋anjAnj（j=1，2，…，n）.

证

根据引理，有

D=ailAil+ai2Ai2+…+ainAin　（i=1，2，…，n）.

类似地，可以得到列的结论，即

D=a1jA1j+a2jA2j+…+anjAnj　（1=1，2，…，n）.

这个定理称为行列式按行（列）展开法则，利用这一法则并结合行列式的性质，可将行列式降阶，从而简化行列式的计算.

下面用此法则，再来计算1.3节例1.8中的行列式

例1.12　计算2n阶行列式

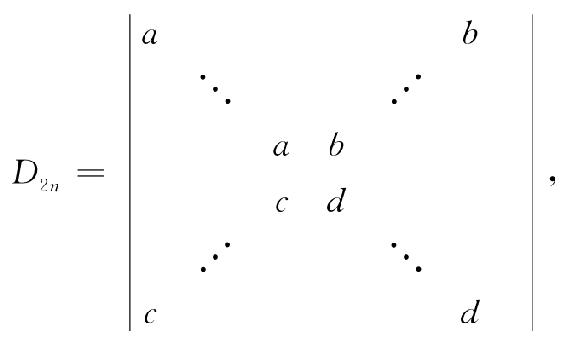
未写出的元素均为0.

解　按第1行展开有

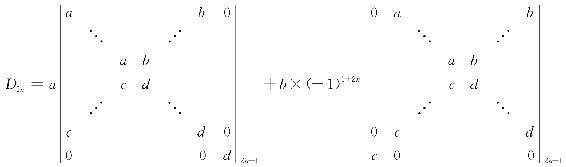
再对上式两个2n-1阶行列式按第2n-1行展开，得

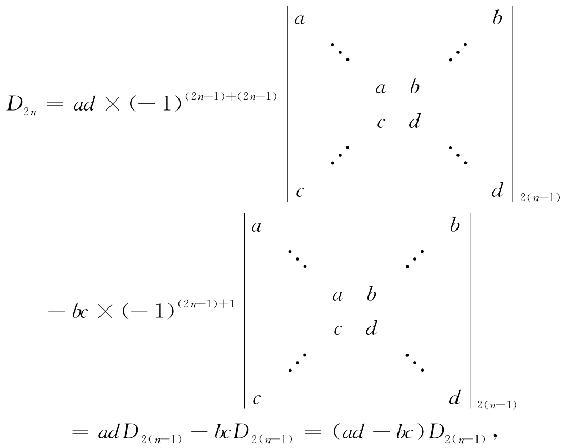
以此作递推公式，得

D2n=（ad-bc）D2（n-1）=（ad-bc）2D2（n-2）=…=（ad-bc）n-1D2=（ad-bc）n.

例1.13　证明范德蒙德（Vandermonde）行列式

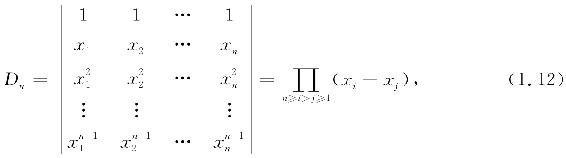
其中，记号“∏”表示全体同类因子的乘积.

证　用数学归纳法证明. 当n=2时，

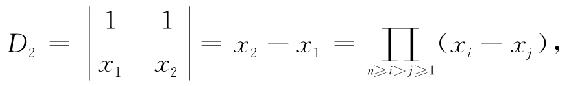
所以当n=2时，式（1.12）成立.

假设式（1.12）对n-1阶范德蒙德行列式成立，要证式（1.12）对n阶范德蒙德行列式也成立. 为此，将Dn降阶，从第n行开始，后一行减前一行的x1倍，得

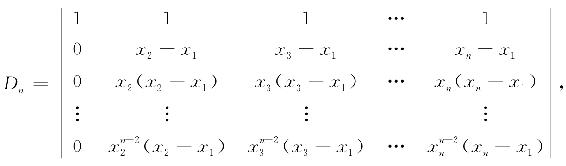
按第1列展开，并提出每一列的公因子（xi-x1），有

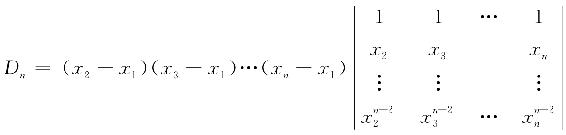
上式右端行列式是n-1阶范德蒙德行列式，由归纳法假设它等于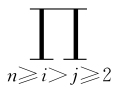（xi-xj），故

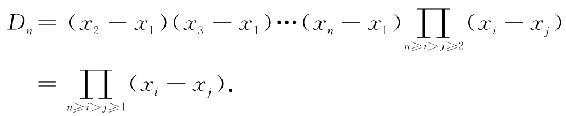
显然，范德蒙德行列式不为零的充要条件是x1，x2，…，xn互不相等.

推论　行列式某一行（列）的元素与另一行（列）的对应元素的代数余子式乘积之和等于零，即

ai1Aj1+ai2Aj2+…+ainAjn=0（i≠j），

或

a1iA1j+a2iA2j+…＋aniAnj=0（i≠j）.

证明略.

综合定理4及其推论，得