2.1 矩阵

2.1　矩阵

有m个方程n个未知数的线性方程组

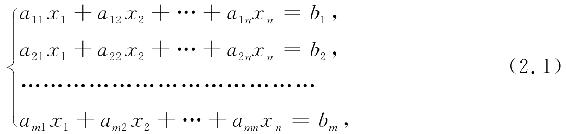
其系数及常数项可以排成m行n+l列的数表

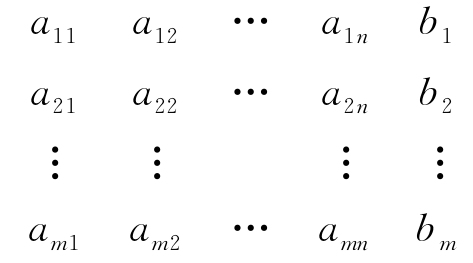
这个数表与方程组有一一对应的关系，于是对方程组的研究就可以转化为对这个数表的研究. 这样的数表我们称为矩阵.

定义1　由m×n个数aij（i=1，2，…，m；j=1，2，…，n）排成m行n列的数表

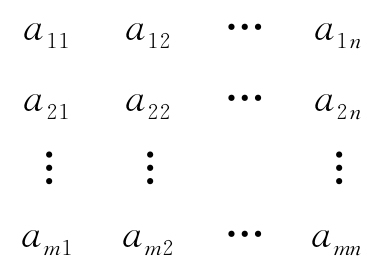
称为m行n列的矩阵，简称m×n矩阵. 为了表示它是一个整体，总是加一个括弧（中括弧或小括弧），并用大写黑体字母表示它，记作

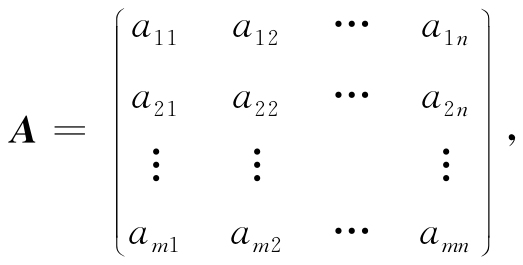
其中，aij示矩阵第i行j列的元素，称为矩阵A的（i，j）元. 以数aij为（i，j）元的矩阵可简记作（aij）或（aij）m×n，m×n二矩阵A也记作Am×n.

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵. 本书中除特别声明外，都是指实矩阵.

几种特殊的矩阵：

①若矩阵只有一行元素，这样的矩阵称为行矩阵，也称为行向量，记作A=（a1，a2…an），为了避免元素间的混淆，行矩阵一般记作A=（a1，a2，…，an）.

②若矩阵只有一列元素，这样的矩阵称为列矩阵，也称为列向量，记作

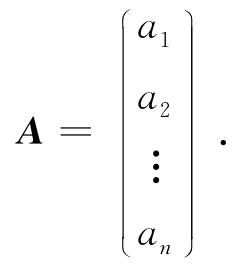
③若矩阵所有的元素都为零，这样的矩阵称为零矩阵，记作O.

④若矩阵的行数与列数相同，即m=n时，这样的矩阵称为n阶方阵，记作

⑤对于n阶方阵，若主对角线以外的元素全部为零，这样的矩阵称为对角矩阵，记作

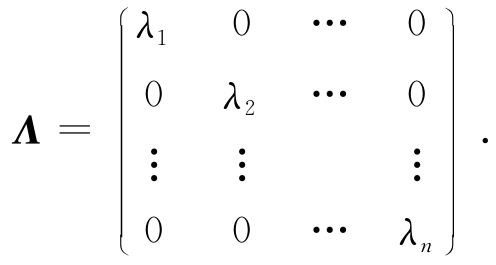
对角矩阵也可记作

A=diag（λ1，λ2，…，λn）.

特殊地，当λ1=λ2=…=λn时，此矩阵称为数量矩阵.

⑥对于n阶方阵，若主对角线上的元素全部为1，其余元素全部为0，这样的矩阵称为单位矩阵，记作

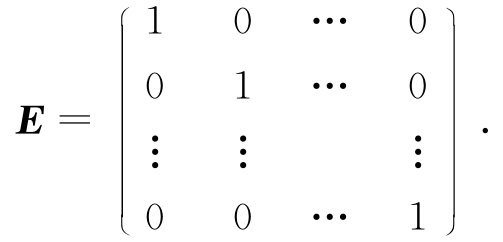
定义2　若两个矩阵的行数与列数分别相等，则称它们为同型矩阵.

若矩阵A与矩阵B为同型矩阵，并且对应的元素相等，则称矩阵A与矩阵B相等，记作

A=B.