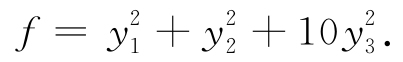6.1 二次型及其标准形

6.1　二次型及其标准形

6.1.1　二次型的概念及其矩阵表示

定义1　含有n个变量x1，x2，…，xn的二次齐次函数

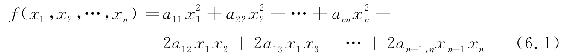
称为二次型.

当aij都为实数时，称f为实二次型；当aij为复数时，称f为复二次型. 这里，我们只讨论实二次型.

取aij=aji，则2aijxixj＝aijxixj+ajixjxi，于是二次型式（（6.1）可以写成

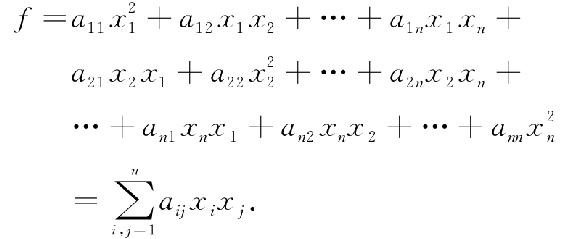
利用矩阵，二次型又可表示为

则二次型可记作

f=xTAx.

（6.2）

因为aij=aji（i，j=1，2，…，n），即AT=A，所以A为对称矩阵，且A的主对角线上的元素恰好是二次型中平方项的系数，而aij（i≠j）恰好是二次型中xixj的系数的一半.

由此可知，任给一个二次型，就唯一地确定一个对称矩阵；反之，任给一个对称矩阵，也可唯一地确定一个二次型. 这样，二次型与对称矩阵之间存在一一对应关系. 因此，可以用对称矩阵讨论二次型，称对称阵A为二次型f的矩阵，也称f为对称阵A的二次型. 矩阵A的秩就称为二次型f的秩.

例如，二次型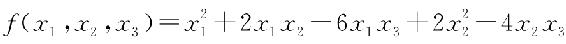的矩阵为

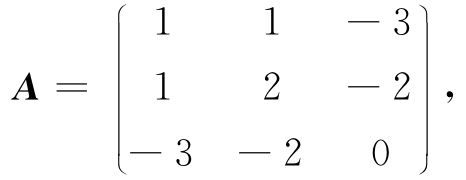
而对称阵

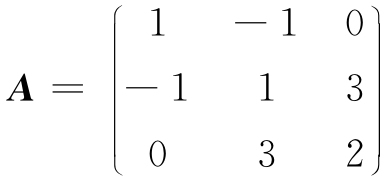
对应的二次型为.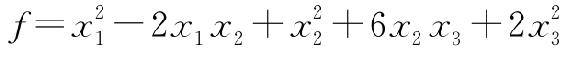

定义2　设A，B为n阶方阵，如果存在n阶可逆矩阵C，使

CTAC=B，

则称A与B合同.

显然，C可逆一定有CT可逆，因此，合同矩阵一定是等价矩阵. 于是合同矩阵具有以下性质：

（i）反身性　A与A合同：

（ii）对称性　若A与B合同，则B与A合同；

（iii）传递性　若A与B合同，B与C合同，则A与C相合同；

（iv）若A与B合同，则R（A）=R（B）.

6.1.2　二次型的标准形

对于二次型，我们讨论的主要问题是：寻求可逆的线性变换

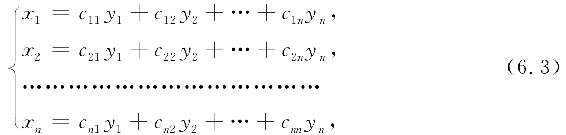
使二次型只含平方项，也就是用（6.3）代入（6.1），可得

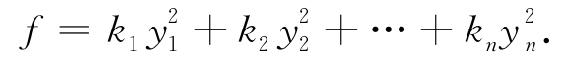
这种只含平方项的二次型，称为二次型的标准形.

记C=（cij），可逆变换（6.3）记作

x=Cy，

代入（6.2）式，有f=xTAx=（Cy）TACy=yT（CTAC）y.

由此可知，要使二次型f经可逆变换x=Cy变成标准形，就是要使

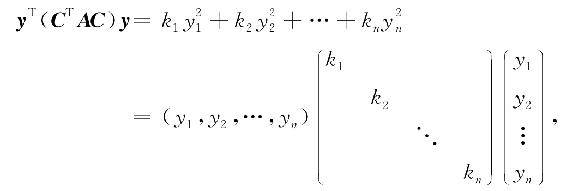
也就是要使CTAC成为对角矩阵. 因此，我们的主要问题就是：对于对称矩阵A，寻找可逆矩阵C，使CTAC为对角矩阵.

由第5章定理8知，任给对称矩阵A，总有正交矩阵P，使P-1AP=PTAP=Λ.把此结论用于二次型，即有

定理1　任给二次型f=xTAx，总有正交变换x=Py，使f化为标准形

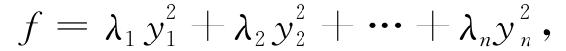
其中λ1，λ2，…λn为f的矩阵A的特征值.

例6.1 求一个正交变换x=Py，将二次型

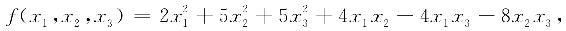
化为标准形.

解　二次型的矩阵为

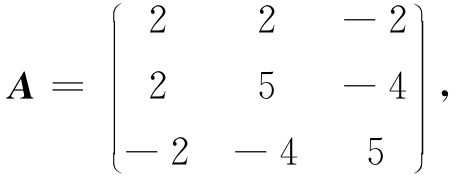
它的特征多项式为

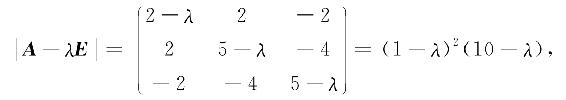
得A的特征值为,λ1=λ2=1，λ3=10.

当λ1=λ2=1时，解齐次线性方程组（A-E）x=0，由

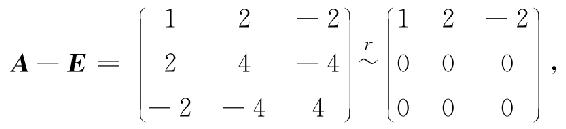
得正交基础解系

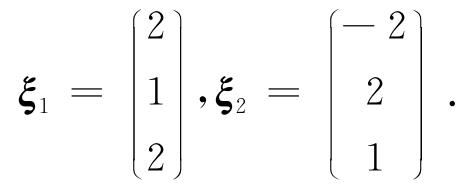
当λ3=10时，解齐次线性方程组（A-10E）x=0，由

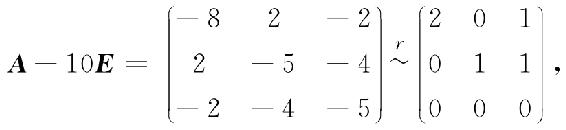
得基础解系

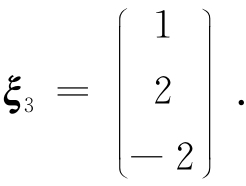
将ξ1，ξ2，ξ3单位化，得

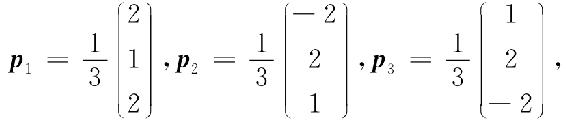
令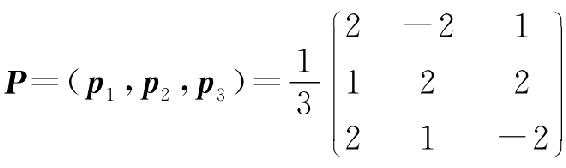，，则P为正交矩阵，且在正交变换x=Py下，可将二次型f化为标准形